tips for creating Graph diagrams

Question

I'd like to programmatically create diagrams like this
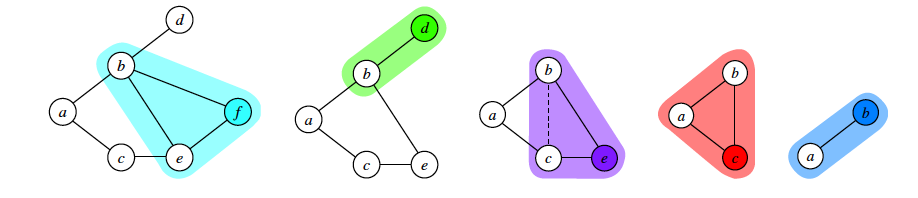
_{(source: yaroslavvb.com)}

I imagine I should use GraphPlot with VertexCoordinateRules, VertexRenderingFunction and EdgeRenderingFunction for the graphs. What should I use for colored beveled backgrounds?

Edit Using mainly Simon's ideas, here's a simplified "less robust" version I ended up using

Needs["GraphUtilities`"];
GraphPlotHighlight[edges_, verts_, color_] := Module[{},
  vpos = Position[VertexList[edges], Alternatives @@ verts];
  coords = Extract[GraphCoordinates[edges], vpos];
  (* add .002 because end-cap disappears when segments are almost colinear *)  
  AppendTo[coords, First[coords] + .002];
  Show[Graphics[{color, CapForm["Round"], JoinForm["Round"], 
     Thickness[.2], Line[coords], Polygon[coords]}],
   GraphPlot[edges], ImageSize -> 150]
  ]

SetOptions[GraphPlot, 
  VertexRenderingFunction -> ({White, EdgeForm[Black], Disk[#, .15], 
      Black, Text[#2, #1]} &), 
  EdgeRenderingFunction -> ({Black, Line[#]} &)];
edges = GraphData[{"Grid", {3, 3}}, "EdgeRules"];
colors = {LightBlue, LightGreen, LightRed, LightMagenta};
vsets = {{8, 5, 2}, {7, 5, 8}, {9, 6, 3}, {8, 1, 2}};
MapThread[GraphPlotHighlight[edges, #1, #2] &, {vsets, colors}]

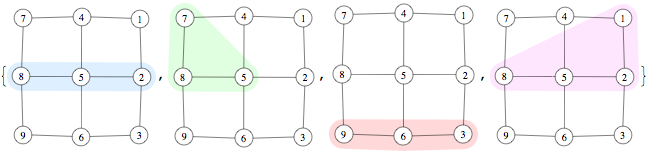
_{(source: yaroslavvb.com)}

Beall

How did you make the graphs used in your question? – Appetizing

Found them on the web. I suspect it was done with some Latex package – Beall

Wolfram talks about a "highlight graph function" at about 9:15 in youtube.com/watch?v=8afAaSiwD78 -- maybe it will be built-in in the next version? – Appetizing

Interesting...btw, looks like TechCon presentation notebooks have been posted (although not Wolfram's) -- wolfram.com/events/techconf2010/speakers.html – Beall

reference.wolfram.com/mathematica/ref/HighlightGraph.html – Appetizing

Answer 1

Generalising Samsdram's answer a bit, I get

GraphPlotHighlight[edges:{((_->_)|{_->_,_})..},hl:{___}:{},opts:OptionsPattern[]]:=Module[{verts,coords,g,sub},
  verts=Flatten[edges/.Rule->List]//.{a___,b_,c___,b_,d___}:>{a,b,c,d};
  g=GraphPlot[edges,FilterRules[{opts}, Options[GraphPlot]]];
  coords=VertexCoordinateRules/.Cases[g,HoldPattern[VertexCoordinateRules->_],2];
  sub=Flatten[Position[verts,_?(MemberQ[hl,#]&)]];
  coords=coords[[sub]];     
  Show[Graphics[{OptionValue[HighlightColor],CapForm["Round"],JoinForm["Round"],Thickness[OptionValue[HighlightThickness]],Line[AppendTo[coords,First[coords]]],Polygon[coords]}],g]
]
Protect[HighlightColor,HighlightThickness];
Options[GraphPlotHighlight]=Join[Options[GraphPlot],{HighlightColor->LightBlue,HighlightThickness->.15}];

Some of the code above could be made a little more robust, but it works:

GraphPlotHighlight[{b->c,a->b,c->a,e->c},{b,c,e},VertexLabeling->True,HighlightColor->LightRed,HighlightThickness->.1,VertexRenderingFunction -> ({White, EdgeForm[Black], Disk[#, .06], 
Black, Text[#2, #1]} &)]

---

EDIT #1: A cleaned up version of this code can be found at http://gist.github.com/663438

EDIT #2: As discussed in the comments below, the pattern that my edges must match is a list of edge rules with optional labels. This is slightly less general than what is used by the GraphPlot function (and by the version in the above gist) where the edge rules are also allowed to be wrapped in a Tooltip.

To find the exact pattern used by GraphPlot I repeatedly used Unprotect[fn];ClearAttributes[fn,ReadProtected];Information[fn] where fn is the object of interest until I found that it used the following (cleaned up) function:

Network`GraphPlot`RuleListGraphQ[x_] := 
  ListQ[x] && Length[x] > 0 && 
    And@@Map[Head[#1] === Rule 
         || (ListQ[#1] && Length[#1] == 2 && Head[#1[[1]]] === Rule) 
         || (Head[#1] === Tooltip && Length[#1] == 2 && Head[#1[[1]]] === Rule)&, 
      x, {1}]

I think that my edges:{((_ -> _) | (List|Tooltip)[_ -> _, _])..} pattern is equivalent and more concise...

Appetizing

what are you trying to match with "edges" pattern? – Beall

The order of the vertices in the GraphicsComplex generated by GraphPlot is simply the order that they occur in edges. My verts=... is just an ugly way of getting that list of vertices in the order that they occur so that I know which coordinates to extract from g and pass to the Graphics command. It's a kludge necessitated by the fact that if VertexLabeling->False then GraphPlot doesn't keep any information about which vertex is which. – Appetizing

ic...it seems you can get around that with VertexList/GraphCoordinates. I was actually asking about edges: pattern in function definition. For instance, it matches {3 -> 4, 4 -> 5, {6 -> 7, 2}} – Beall

@Yaroslav I didn't know about VertexList -- that is a lot neater. As for the pattern, that's the same pattern the GraphPlot uses when plotting a list of edges (as opposed to an adjacency matrix). – Appetizing

How can you tell that's the pattern they use? – Beall

@Yaroslav I can't... but it does the same thing as what's described in the documentation. (of course, correct me if I'm wrong) – Appetizing

ah, I see, so it's for edges with optional label – Beall

Yep, edges with optional labels. Actually, a bit of digging and you find that Mma uses the check: NetworkGraphPlotRuleListGraphQ[x_]:=!NetworkGraphPlotDumpPrivatebigMatrixQ[x]&&ListQ[x]&&Length[x]>0&&And@@Map[Head[#1]===Rule||(ListQ[#1]&&Length[#1]==2&&Head[#1[[1]]]===Rule)||(Head[#1]===Tooltip&&Length[#1]==2&&Head[#1[[1]]]===Rule)&,x,{1}]` which is slightly more general than mine, since it allows for the Rules to be wrapped in Tooltips. – Appetizing

@Yaroslav 3 steps (sorry about the mess...) (1)Unprotect[GraphPlot];ClearAttributes[GraphPlot,ReadProtected];Information[GraphPlot] (2)Unprotect[NetworkGraphPlotDumpPrivateRuleListGraphQ];ClearAttributes[NetworkGraphPlotDumpPrivateRuleListGraphQ,ReadProtected];Information[NetworkGraphPlotDumpPrivateRuleListGraphQ]` (3)Unprotect[NetworkGraphPlotRuleListGraphQ];ClearAttributes[NetworkGraphPlotRuleListGraphQ,ReadProtected];Information[NetworkGraphPlotRuleListGraphQ] – Appetizing

@Appetizing Your last two comments are very interesting! Could you edit your answer and include them? Here, in the comments, they are almost hidden for future readers, and I guess it took you a lot of effort to dig that out. – Iced

@belisarius Thanks. It's not really part of my answer -- but you are right, these things do get lost in the comments. I've edited my answer. – Appetizing

Answer 2

For simple examples where you are only connecting two nodes (like your example on the far right), you can draw lines with capped end points like this.

vertices = {a, b};
Coordinates = {{0, 0}, {1, 1}};
GraphPlot[{a -> b}, VertexLabeling -> True, 
 VertexCoordinateRules -> 
  MapThread[#1 -> #2 &, {vertices, Coordinates}], 
 Prolog -> {Blue, CapForm["Round"], Thickness[.1], Line[Coordinates]}]

For more complex examples (like second from the right) I would recommend drawing a polygon using the vertex coordinates and then tracing the edge of the polygon with a capped line. I couldn't find a way to add a beveled edge directly to a polygon. When tracing the perimeter of the polygon you need to add the coordinate of the first vertex to the end of the line segment that the line makes the complete perimeter of the polygon. Also, there are two separate graphics directives for lines CapForm, which dictates whether to bevel the ends of the line, and JoinForm, which dictates whether to bevel the intermediate points of the line.

vertices = {a, b, c};
Coordinates = {{0, 0}, {1, 1}, {1, -1}};
GraphPlot[{a -> b, b -> c, c -> a}, VertexLabeling -> True, 
 VertexCoordinateRules -> 
  MapThread[#1 -> #2 &, {vertices, Coordinates}], 
 Prolog -> {Blue, CapForm["Round"], JoinForm["Round"], Thickness[.15],
    Line[AppendTo[Coordinates, First[Coordinates]]], 
   Polygon[Coordinates]}]

Ethnocentrism

How can you highlight only a subset of vertices using this? – Appetizing

Answer 3

JoinForm["Round"] will round the joins of line segments.

You'll want a filled polygon around the centers of the vertices in the colored region, then a JoinForm["Round"], ..., Line[{...}] to get the rounded corners.

Consider

foo = GraphPlot[{a -> b, a -> c, b -> d, b -> e, b -> f, c -> e, e -> f}, 
    VertexRenderingFunction -> 
    ({White, EdgeForm[Black], Disk[#, .1], Black, Text[#2, #1]} &)]
Show[
    Graphics[{
      RGBColor[0.6, 0.8, 1, 1],
      Polygon[foo[[1, 1, 1, 1, 1, {2, 5, 6, 2}]]],
      JoinForm["Round"], Thickness[0.2],
      Line[foo[[1, 1, 1, 1, 1, {2, 5, 6, 2}]]]
    }],
    foo
]

where foo[[1,1,1,1,1]] is the list of vertex centers and {2,5,6} pulls out the {b,e,f} vertices. ({2,5,6,2} closes the line back at its starting point.)

There's plenty of room for prettifying, but I think this covers the ingredient you didn't mention above.

Showroom