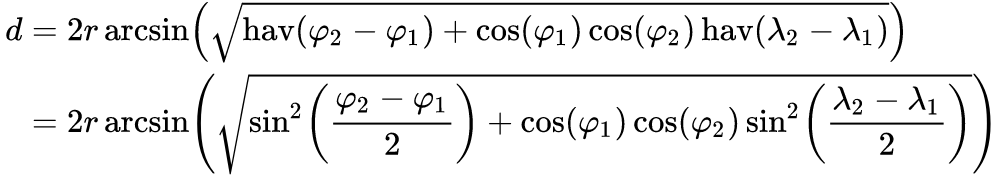Calculating Distance between two Latitude and Longitude GeoCoordinates

Question

I'm calculating the distance between two GeoCoordinates. I'm testing my app against 3-4 other apps. When I'm calculating distance, I tend to get an average of 3.3 miles for my calculation whereas other apps are getting 3.5 miles. It's a big difference for the calculation I'm trying to perform. Are there any good class libraries out there for calculating distance? I'm calculating it like this in C#:

public static double Calculate(double sLatitude,double sLongitude, double eLatitude, 
                               double eLongitude)
{
    var radiansOverDegrees = (Math.PI / 180.0);

    var sLatitudeRadians = sLatitude * radiansOverDegrees;
    var sLongitudeRadians = sLongitude * radiansOverDegrees;
    var eLatitudeRadians = eLatitude * radiansOverDegrees;
    var eLongitudeRadians = eLongitude * radiansOverDegrees;

    var dLongitude = eLongitudeRadians - sLongitudeRadians;
    var dLatitude = eLatitudeRadians - sLatitudeRadians;

    var result1 = Math.Pow(Math.Sin(dLatitude / 2.0), 2.0) + 
                  Math.Cos(sLatitudeRadians) * Math.Cos(eLatitudeRadians) * 
                  Math.Pow(Math.Sin(dLongitude / 2.0), 2.0);

    // Using 3956 as the number of miles around the earth
    var result2 = 3956.0 * 2.0 * 
                  Math.Atan2(Math.Sqrt(result1), Math.Sqrt(1.0 - result1));

    return result2;
}

What could I be doing wrong? Should I calculate it in km first and then convert to miles?

Dilworth

Earth mean radius = 6,371km = 3958.76 miles – Broadleaved

#28428 – Broadleaved

shouldn't this be on gis.stackexchange.com – Uprising

It could have, but my question pertains more to calculating this on a Windows Phone which is a bit different. The formula is the same, but newer method calls like the DistanceTo method aren't necessarily available. – Dilworth

Suggest you store pi/180 so you don't have to keep repeating the calculation. – Zayas

@ChrisCaviness pretty sure any competent compiler will perform constant evaluation to avoid repeated calculation of that. – Reichard

Answer 1

The GeoCoordinate class (.NET Framework 4 and higher) already has GetDistanceTo method.

var sCoord = new GeoCoordinate(sLatitude, sLongitude);
var eCoord = new GeoCoordinate(eLatitude, eLongitude);

return sCoord.GetDistanceTo(eCoord);

The distance is in meters.

You need to reference System.Device.

Heilungkiang

Nigel, are you sure that the DistanceTo method will work on the phone? I thought it used the 2.0 version of GeoCoordinate for WP7. – Dilworth

I did check this and the GeoCordinate for the device has a GetDistanceTo method which is what you had referenced (but not what you have above). No big deal. I'm going to test this out to see if the built in calculation is any better. Thanks Nigel! – Dilworth

I might ask a wrong question, but in what unit is the result? Is it Miles, or Kilometers. I can't find it anywhere. – Pinkston

@SaeedNeamati - was looking for this too, according to msdn.microsoft.com/en-us/library/… - it's in metres. – Sinaloa

Yes, GeoCoordinate.GetDistanceTo() returns the value in meters. For me, in the USA, if it's less than 1610, I convert it to feet (meters * 3.28084) otherwise I convert to miles (meters * 0.000621371). Accuracy is more than good enough for my purposes. – India

could you please convert, the distance in kilometers? – Darcie

@BanwariYadav you already get the result in metres, just divide the result by 1000 to get the distance in kilometers... – Leeuwarden

Can anyone suggest me how to calculate the Estimated time of arrival from point 1 to point 2 with 30 miles/h speed – Continuance

Yes indeed, using the .NET library is the best option if working with .NET/C#. I have tried many snippets in internet and compared it to a calculation made by Azure Maps, this return the most accurate result. – Irrupt

what unit does GetDistanceTo() give? is it in kilometer or miles? – Rog

Answer 2

GetDistance is the best solution, but in many cases we can't use this Method (e.g. Universal App)

• Pseudocode of the Algorithm to calculate the distance between to coorindates:

  public static double DistanceTo(double lat1, double lon1, double lat2, double lon2, char unit = 'K')
  {
      double rlat1 = Math.PI*lat1/180;
      double rlat2 = Math.PI*lat2/180;
      double theta = lon1 - lon2;
      double rtheta = Math.PI*theta/180;
      double dist =
          Math.Sin(rlat1)*Math.Sin(rlat2) + Math.Cos(rlat1)*
          Math.Cos(rlat2)*Math.Cos(rtheta);
      dist = Math.Acos(dist);
      dist = dist*180/Math.PI;
      dist = dist*60*1.1515;
  
      switch (unit)
      {
          case 'K': //Kilometers -> default
              return dist*1.609344;
          case 'N': //Nautical Miles 
              return dist*0.8684;
          case 'M': //Miles
              return dist;
      }
  
      return dist;
  }
  

• Real World C# Implementation, which makes use of an Extension Methods

  Usage:

  var distance = new Coordinates(48.672309, 15.695585)
                  .DistanceTo(
                      new Coordinates(48.237867, 16.389477),
                      UnitOfLength.Kilometers
                  );
  

  Implementation:

  public class Coordinates
  {
      public double Latitude { get; private set; }
      public double Longitude { get; private set; }
  
      public Coordinates(double latitude, double longitude)
      {
          Latitude = latitude;
          Longitude = longitude;
      }
  }
  public static class CoordinatesDistanceExtensions
  {
      public static double DistanceTo(this Coordinates baseCoordinates, Coordinates targetCoordinates)
      {
          return DistanceTo(baseCoordinates, targetCoordinates, UnitOfLength.Kilometers);
      }
  
      public static double DistanceTo(this Coordinates baseCoordinates, Coordinates targetCoordinates, UnitOfLength unitOfLength)
      {
          var baseRad = Math.PI * baseCoordinates.Latitude / 180;
          var targetRad = Math.PI * targetCoordinates.Latitude/ 180;
          var theta = baseCoordinates.Longitude - targetCoordinates.Longitude;
          var thetaRad = Math.PI * theta / 180;
  
          double dist =
              Math.Sin(baseRad) * Math.Sin(targetRad) + Math.Cos(baseRad) *
              Math.Cos(targetRad) * Math.Cos(thetaRad);
          dist = Math.Acos(dist);
  
          dist = dist * 180 / Math.PI;
          dist = dist * 60 * 1.1515;
  
          return unitOfLength.ConvertFromMiles(dist);
      }
  }
  
  public class UnitOfLength
  {
      public static UnitOfLength Kilometers = new UnitOfLength(1.609344);
      public static UnitOfLength NauticalMiles = new UnitOfLength(0.8684);
      public static UnitOfLength Miles = new UnitOfLength(1);
  
      private readonly double _fromMilesFactor;
  
      private UnitOfLength(double fromMilesFactor)
      {
          _fromMilesFactor = fromMilesFactor;
      }
  
      public double ConvertFromMiles(double input)
      {
          return input*_fromMilesFactor;
      }
  } 
  

Alcus

Can you provide the formula used for this calculus or maybe some comments about what line does? what would I have to change to directly have the resulting distance in Km instead of miles without having to convert? – Hammerfest

Worked great in my UWP app where I cannot use GeoCoordinate. – Saturday

calculation is 95% true. the below function is 100% accurate: https://mcmap.net/q/46813/-calculating-distance-between-two-latitude-and-longitude-geocoordinates – Passible

Answer 3

And here, for those still not satisfied (like me), the original code from .NET-Frameworks GeoCoordinate class, refactored into a standalone method:

public double GetDistance(double longitude, double latitude, double otherLongitude, double otherLatitude)
{
    var d1 = latitude * (Math.PI / 180.0);
    var num1 = longitude * (Math.PI / 180.0);
    var d2 = otherLatitude * (Math.PI / 180.0);
    var num2 = otherLongitude * (Math.PI / 180.0) - num1;
    var d3 = Math.Pow(Math.Sin((d2 - d1) / 2.0), 2.0) + Math.Cos(d1) * Math.Cos(d2) * Math.Pow(Math.Sin(num2 / 2.0), 2.0);
    
    return 6376500.0 * (2.0 * Math.Atan2(Math.Sqrt(d3), Math.Sqrt(1.0 - d3)));
}

Agouti

Beatiful answer, I'd like to point out that the resulting distance is in meters. as stated in official documentation – Pahang

Thanks! I was looking for the actual radius of earth used in the GeoCoordinate class. – Amon

Minor optimization, or for easier reading, could pre-compute pi/180 double oneDegree = Math.PI / 180.0; ? – Mistrot

@Mistrot Thanks for your reply. I would like to leave the answer as it is, because this is the original .NET code. Anyone can feel free to follow your suggestion though, of course. – Agouti

Works like a charm, simplest answer ;) – Emperor

I'm not sure on this one...I entered some coords (43/-86 range) and this code said the distance was 926M. Using the Haversine code below the result was 13000M. The 13KM is way more accurate. I understand these are approximations and all, but these are typical distances, not on the poles, etc. Maybe I screwed something up, but it was a cut/paste from here into the code. – Locate

It's worth noting that the method in the provided answer calculates Great Circle distance :) – Ecclesiastical

Also worth noting the parameters are the other way round to every other method on this page, that's probably what you did @Locate – Duane

Answer 4

Here is the JavaScript version guys and gals

function distanceTo(lat1, lon1, lat2, lon2, unit) {
      var rlat1 = Math.PI * lat1/180
      var rlat2 = Math.PI * lat2/180
      var rlon1 = Math.PI * lon1/180
      var rlon2 = Math.PI * lon2/180
      var theta = lon1-lon2
      var rtheta = Math.PI * theta/180
      var dist = Math.sin(rlat1) * Math.sin(rlat2) + Math.cos(rlat1) * Math.cos(rlat2) * Math.cos(rtheta);
      dist = Math.acos(dist)
      dist = dist * 180/Math.PI
      dist = dist * 60 * 1.1515
      if (unit=="K") { dist = dist * 1.609344 }
      if (unit=="N") { dist = dist * 0.8684 }
      return dist
}

Weir

Wha do you need rlon1 and `rlon2´ for? – Dasie

Answer 5

For those who are using Xamarin and don't have access to the GeoCoordinate class, you can use the Android Location class instead:

public static double GetDistanceBetweenCoordinates (double lat1, double lng1, double lat2, double lng2) {
            var coords1 = new Location ("");
            coords1.Latitude = lat1;
            coords1.Longitude = lng1;
            var coords2 = new Location ("");
            coords2.Latitude = lat2;
            coords2.Longitude = lng2;
            return coords1.DistanceTo (coords2);
        }

Turgite

Answer 6

This is an old question, nevertheless the answers did not satisfy me regarding to performance and optimization.

Here my optimized C# variant (distance in km, without variables and redundant calculations, very close to mathematical expression of Haversine Formular https://en.wikipedia.org/wiki/Haversine_formula).

Inspired by: https://rosettacode.org/wiki/Haversine_formula#C.23

public static class Haversine
{
    public static double Calculate(double lat1, double lon1, double lat2, double lon2)
    {
        double rad(double angle) => angle * 0.017453292519943295769236907684886127d; // = angle * Math.Pi / 180.0d
        double havf(double diff) => Math.Pow(Math.Sin(rad(diff) / 2d), 2); // = sin²(diff / 2)
        return 12745.6 * Math.Asin(Math.Sqrt(havf(lat2 - lat1) + Math.Cos(rad(lat1)) * Math.Cos(rad(lat2)) * havf(lon2 - lon1))); // earth radius 6.372,8‬km x 2 = 12745.6
    }
}

Corrigendum

Absolutely great answer if you're looking for performance. I have run this on hundreds of millions of points. – Cajeput

Answer 7

There's this library GeoCoordinate for these platforms:

• Mono
• .NET 4.5
• .NET Core
• Windows Phone 8.x
• Universal Windows Platform
• Xamarin iOS
• Xamarin Android

Installation is done via NuGet:

PM> Install-Package GeoCoordinate

Usage

GeoCoordinate pin1 = new GeoCoordinate(lat, lng);
GeoCoordinate pin2 = new GeoCoordinate(lat, lng);

double distanceBetween = pin1.GetDistanceTo(pin2);

The distance between the two coordinates, in meters.

Monaxial

Answer 8

When CPU/math computing power is limited:

There are times (such as in my work) when computing power is scarce (e.g. no floating point processor, working with small microcontrollers) where some trig functions can take an exorbitant amount of CPU time (e.g. 3000+ clock cycles), so when I only need an approximation, especially if if the CPU must not be tied up for a long time, I use this to minimize CPU overhead:

/**------------------------------------------------------------------------
 * \brief  Great Circle distance approximation in km over short distances.
 *
 * Can be off by as much as 10%.
 *
 * approx_distance_in_mi = sqrt(x * x + y * y)
 *
 * where x = 69.1 * (lat2 - lat1)
 * and y = 69.1 * (lon2 - lon1) * cos(lat1/57.3)
 *//*----------------------------------------------------------------------*/
double    ApproximateDisatanceBetweenTwoLatLonsInKm(
                  double lat1, double lon1,
                  double lat2, double lon2
                  ) {
    double  ldRadians, ldCosR, x, y;

    ldRadians = (lat1 / 57.3) * 0.017453292519943295769236907684886;
    ldCosR = cos(ldRadians);
    x = 69.1 * (lat2 - lat1);
    y = 69.1 * (lon2 - lon1) * ldCosR;

    return sqrt(x * x + y * y) * 1.609344;  /* Converts mi to km. */
}

Credit goes to https://github.com/kristianmandrup/geo_vectors/blob/master/Distance%20calc%20notes.txt.

Trahern

Answer 9

Based on Elliot Wood's function, and if anyone is interested in a C function, this one is working...

#define SIM_Degree_to_Radian(x) ((float)x * 0.017453292F)
#define SIM_PI_VALUE                         (3.14159265359)

float GPS_Distance(float lat1, float lon1, float lat2, float lon2)
{
   float theta;
   float dist;

   theta = lon1 - lon2;

   lat1 = SIM_Degree_to_Radian(lat1);
   lat2 = SIM_Degree_to_Radian(lat2);
   theta = SIM_Degree_to_Radian(theta);

   dist = (sin(lat1) * sin(lat2)) + (cos(lat1) * cos(lat2) * cos(theta));
   dist = acos(dist);

//   dist = dist * 180.0 / SIM_PI_VALUE;
//   dist = dist * 60.0 * 1.1515;
//   /* Convert to km */
//   dist = dist * 1.609344;

   dist *= 6370.693486F;

   return (dist);
}

You may change it to double. It returns the value in km.

Usquebaugh

Answer 10

Results comparison with Bench Marks

You really need to look at the variations in results and you need benchmarks.

I took several answers on this page plus an unknown and compared them to the code that I had written 20 years ago.

I used these coordinates for the test: 32.9697, -96.80322 and 29.46786, -98.53506

Here is my method:

 public static double CalculateDistanceBetweenCoordinates(double fromLatitude, double fromLongitude,
    double toLatitude, double toLongitude)
{
    double x = 69.1 * (toLatitude - fromLatitude);
    double y = 69.1 * (toLongitude - fromLongitude) * Math.Cos(fromLatitude / 57.3);

    // Convert to KM by multiplying 1.609344
    return (Math.Sqrt(x * x + y * y) * 1.609344);
}

Here are the results in KM:

• 422.73893139401383 // My Code *My code and Yanga produce identical results.
• 421.6152868008663 // by Leitner
• 422.8787129776151 // By JanW
• 422.73893139401383 // By Yanga
• 422.7592707099537 // Unknown

You can see that they are all very close except the answer by Leitner which is off about 1km. I also checked two on-line calculators and their answers were 421.8 and 422.8 so off by 1km.

And here are the Benchmarks running 1,000,000 iterations using BenchmarkDotNet 0.13.2 (note that I left out the answer by Marc):

BenchmarkDotNet=v0.13.2, OS=Windows 11 (10.0.22000.978/21H2)

Intel Core i7-8700 CPU 3.20GHz (Coffee Lake), 1 CPU, 12 logical and 6 physical cores .NET SDK=6.0.401 [Host] : .NET 6.0.9 (6.0.922.41905), X64 RyuJIT AVX2 DefaultJob : .NET 6.0.9 (6.0.922.41905), X64 RyuJIT AVX2

Method	Mean	Error	StdDev	Ratio	RatioSD	Rank	Allocated	Alloc Ratio
MyCode	239.6 us	2.56 us	2.14 us	1.00	0.00	1	-	NA
Other	34,014.2 us	405.67 us	379.46 us	142.25	1.69	2	32 B	NA
Leitner	46,749.4 us	390.52 us	346.19 us	195.23	2.50	3	44 B	NA
Yanga	48,360.2 us	955.85 us	1,062.43 us	202.75	4.24	4	44 B	NA
JanW	97,399.6 us	708.25 us	627.84 us	406.54	4.79	5	592 B	NA

For reference here is the other method I found:

 return 12742 * Math.Asin(Math.Sqrt(0.5 - Math.Cos((lat2 - lat1) * 0.017453292519943295) / 2 + Math.Cos(lat1 * 0.017453292519943295) * Math.Cos(lat2 * 0.017453292519943295) * (1 - Math.Cos((lon2 - lon1) * 0.017453292519943295)) / 2));

In summary, there will always be variations depending on how the distance is calculated. But for performance my method is by far the fastest and with zero allocated memory.

Ie

What's going on with your test of Marc's method is that, compared to the others, it expects longitude before latitude. Doing that will yield 423.12423319447634. – Nosy

Well done!! Over 100X faster! That matters when CPU time is limited, as is the case in many microcontroller applications!! – Trahern

@Nosy Thank you. I must have mixed up the lat and long. – Ie

Answer 11

You can use this function :

Source : https://www.geodatasource.com/developers/c-sharp

private double distance(double lat1, double lon1, double lat2, double lon2, char unit) {
  if ((lat1 == lat2) && (lon1 == lon2)) {
    return 0;
  }
  else {
    double theta = lon1 - lon2;
    double dist = Math.Sin(deg2rad(lat1)) * Math.Sin(deg2rad(lat2)) + Math.Cos(deg2rad(lat1)) * Math.Cos(deg2rad(lat2)) * Math.Cos(deg2rad(theta));
    dist = Math.Acos(dist);
    dist = rad2deg(dist);
    dist = dist * 60 * 1.1515;
    if (unit == 'K') {
      dist = dist * 1.609344;
    } else if (unit == 'N') {
      dist = dist * 0.8684;
    }
    return (dist);
  }
}

//:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
//::  This function converts decimal degrees to radians             :::
//:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
private double deg2rad(double deg) {
  return (deg * Math.PI / 180.0);
}

//:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
//::  This function converts radians to decimal degrees             :::
//:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
private double rad2deg(double rad) {
  return (rad / Math.PI * 180.0);
}

Console.WriteLine(distance(32.9697, -96.80322, 29.46786, -98.53506, "M"));
Console.WriteLine(distance(32.9697, -96.80322, 29.46786, -98.53506, "K"));
Console.WriteLine(distance(32.9697, -96.80322, 29.46786, -98.53506, "N"));

Takeshi

Works perfectly! Thanks! – Pinto

Answer 12

Calculating Distance between Latitude and Longitude points...

        double Lat1 = Convert.ToDouble(latitude);
        double Long1 = Convert.ToDouble(longitude);

        double Lat2 = 30.678;
        double Long2 = 45.786;
        double circumference = 40000.0; // Earth's circumference at the equator in km
        double distance = 0.0;
        double latitude1Rad = DegreesToRadians(Lat1);
        double latititude2Rad = DegreesToRadians(Lat2);
        double longitude1Rad = DegreesToRadians(Long1);
        double longitude2Rad = DegreesToRadians(Long2);
        double logitudeDiff = Math.Abs(longitude1Rad - longitude2Rad);
        if (logitudeDiff > Math.PI)
        {
            logitudeDiff = 2.0 * Math.PI - logitudeDiff;
        }
        double angleCalculation =
            Math.Acos(
              Math.Sin(latititude2Rad) * Math.Sin(latitude1Rad) +
              Math.Cos(latititude2Rad) * Math.Cos(latitude1Rad) * Math.Cos(logitudeDiff));
        distance = circumference * angleCalculation / (2.0 * Math.PI);
        return distance;

Yamauchi

Answer 13

Try this:

    public double getDistance(GeoCoordinate p1, GeoCoordinate p2)
    {
        double d = p1.Latitude * 0.017453292519943295;
        double num3 = p1.Longitude * 0.017453292519943295;
        double num4 = p2.Latitude * 0.017453292519943295;
        double num5 = p2.Longitude * 0.017453292519943295;
        double num6 = num5 - num3;
        double num7 = num4 - d;
        double num8 = Math.Pow(Math.Sin(num7 / 2.0), 2.0) + ((Math.Cos(d) * Math.Cos(num4)) * Math.Pow(Math.Sin(num6 / 2.0), 2.0));
        double num9 = 2.0 * Math.Atan2(Math.Sqrt(num8), Math.Sqrt(1.0 - num8));
        return (6376500.0 * num9);
    }

Bivalve

Answer 14

You can use System.device.Location:

System.device.Location.GeoCoordinate gc = new System.device.Location.GeoCoordinate(){
Latitude = yourLatitudePt1,
Longitude = yourLongitudePt1
};

System.device.Location.GeoCoordinate gc2 = new System.device.Location.GeoCoordinate(){
Latitude = yourLatitudePt2,
Longitude = yourLongitudePt2
};

Double distance = gc2.getDistanceTo(gc);

good luck

Procure

Answer 15

CoordinateSharp does this well. The returned Distance object gives you many different measurements to choose from.

You can even specify if you want Haversine (spherical earth, more efficient/less accurate) or Vincenty (ellipsoidal earth, less efficient/more accurate) calculations via overload methods.

using CoordinateSharp;

//

Coordinate c1 = new Coordinate(45,75);
Coordinate c2 = new Coordinate(45.5,75.1);

Distance d = new Distance(c1,c2);
        
d.Kilometers; //56.145
d.Meters; //56145
d.Miles; //34.88
d.NauticalMiles; //30.16
d.Feet; //184,205

Oilstone