Well, as usual I'm late to the game, but what's a decade between friends?
Plus this answer based on (play trumpets) RECURSION and generalizes the above question to arbitrary d-dimensional lattices of size N1 x N2 x ... x Nd.
The solution is itself a generalization of the method used for hypercubes described in https://mcmap.net/q/471330/-generating-distanced-matrix-for-an-n-dimensional-hypercube
I tend to write pedagogically, so don't hold it against me and please forgive the notation as this is one of the few SO's that doesn't support LaTeX.
We'll first investigate a simple example and think about it with pictures.
Then we'll turn those pictures into maths, and finally convert the maths into an algorithm.
Ready?
Imagine a 4x3x2 lattice. How can we build it "from the ground up?"
One way of doing so is to start with a 1d lattice: a graph with four vertices and 3 edges:
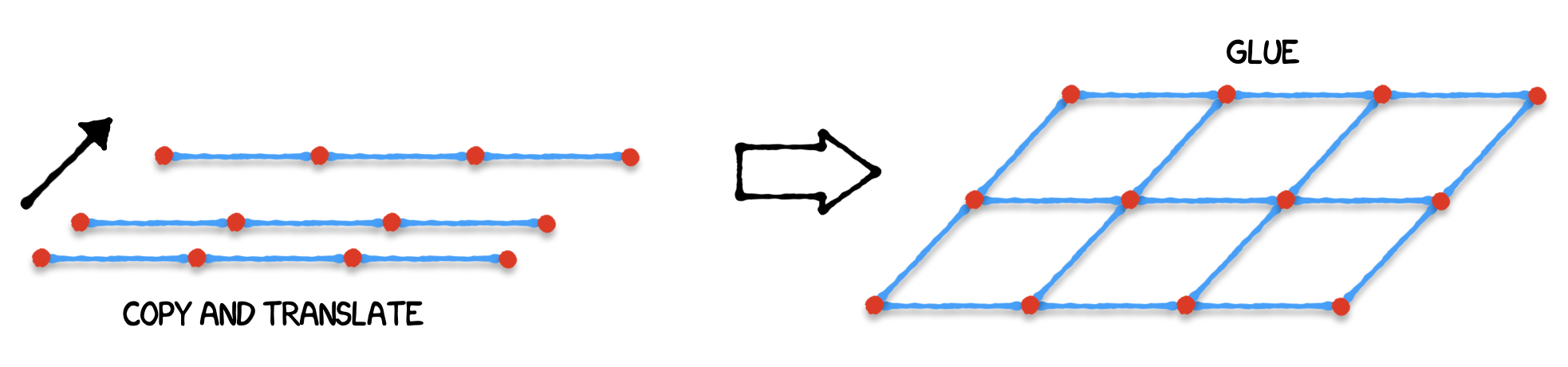
![A 1-dimensional lattice]() Cool, that was easy. Now let's extend this to a 2d lattice that is 4x3.
We do so by making 3-1 copies of the 1d lattice, translate them, and then glue all the copies together into a 2d lattice:
Cool, that was easy. Now let's extend this to a 2d lattice that is 4x3.
We do so by making 3-1 copies of the 1d lattice, translate them, and then glue all the copies together into a 2d lattice:
![A 2-dimensional lattics]() I bet you can see where this is going. To finish we make 2-1 copies of our 2d lattice, and glue them together:
I bet you can see where this is going. To finish we make 2-1 copies of our 2d lattice, and glue them together:
![A 3-dimensional lattice]() Ta da!
Ta da!
It should be clear that you can make a d-dimensional lattice with whatever size you want similarly.
Now, how do we convert this pictorial process into maths?
We'll need tools to copy and glue adjacency matrices together.
Fortunately for us, all we need is the Kronecker product which has the awesome power to do both.
AND it's been implemented in like every linear algebra library that's worth a damn.
Before showing you how to use the Kronecker product, we need to first understand the adjacency matrix of a 1d lattice of length N.
That shouldn't be too hard: vertex 1 is only connected to vertex 2, vertex N is only connected to N-1, and every in between vertex k is connected to both k+1 and k-1.
So the adjacency matrix reads:
![enter image description here]() Also, the identity matrix with N 1's on the diagonal is denoted 1(N), and given M(k-1) = N1 * N2 * ... * N(k-1).
Also, the identity matrix with N 1's on the diagonal is denoted 1(N), and given M(k-1) = N1 * N2 * ... * N(k-1).
Say you know the adjacency matrix of a N1 x N2 x ... x N(k-1) lattice, call it A(k-1).
Then to make the adjacency matrix for the N1 x N2 x ... x N(k-1) x Nk lattice we first take Nk replicas of A(k-1).
Then we take the same vertex in each replica, and glue them sequentially together with edges to form a 1d lattice.
The resulting adjacency matrix has the form
![enter image description here]() If you're having trouble parsing the right hand side, the first term corresponds to the Nk copies of the (k-1)d lattice; that's all those diagonal terms in the middle matrix.
Notice how all the 1(M(k-1))'s are in positions identical to what we just saw for the 1-d lattice: these are the edges that glue together the replicated vertices.
And that's that, we have a recursive way of constructing a lattice.
The base case is, of course, the 1d lattice.
If you're having trouble parsing the right hand side, the first term corresponds to the Nk copies of the (k-1)d lattice; that's all those diagonal terms in the middle matrix.
Notice how all the 1(M(k-1))'s are in positions identical to what we just saw for the 1-d lattice: these are the edges that glue together the replicated vertices.
And that's that, we have a recursive way of constructing a lattice.
The base case is, of course, the 1d lattice.
Here's MATLAB implementation that you can translate into your favorite programming language. It takes as input a vector of positive integers, dims (the number of lattice points in each dimension), and spits out the adjacency matrix.
function L = LATTICE(dims)
if length(dims) == 1
L = sparse(eye(dims));
L = circshift(L,1,1) + circshift(L,1,2);
if dims > 2
L(1,end) = 0; L(end,1) = 0;
end
else
m = prod(dims(1:(end-1));
L = kron(eye(dims(end)),LATTICE(dims(1:(end-1)) + ...
kron(LATTICE(dims(end)),eye(m));
end
end
Note the use of sparse matrices. You should use any analogous structure, just don't make a huge lattice and try to look at the full matrix, ok?
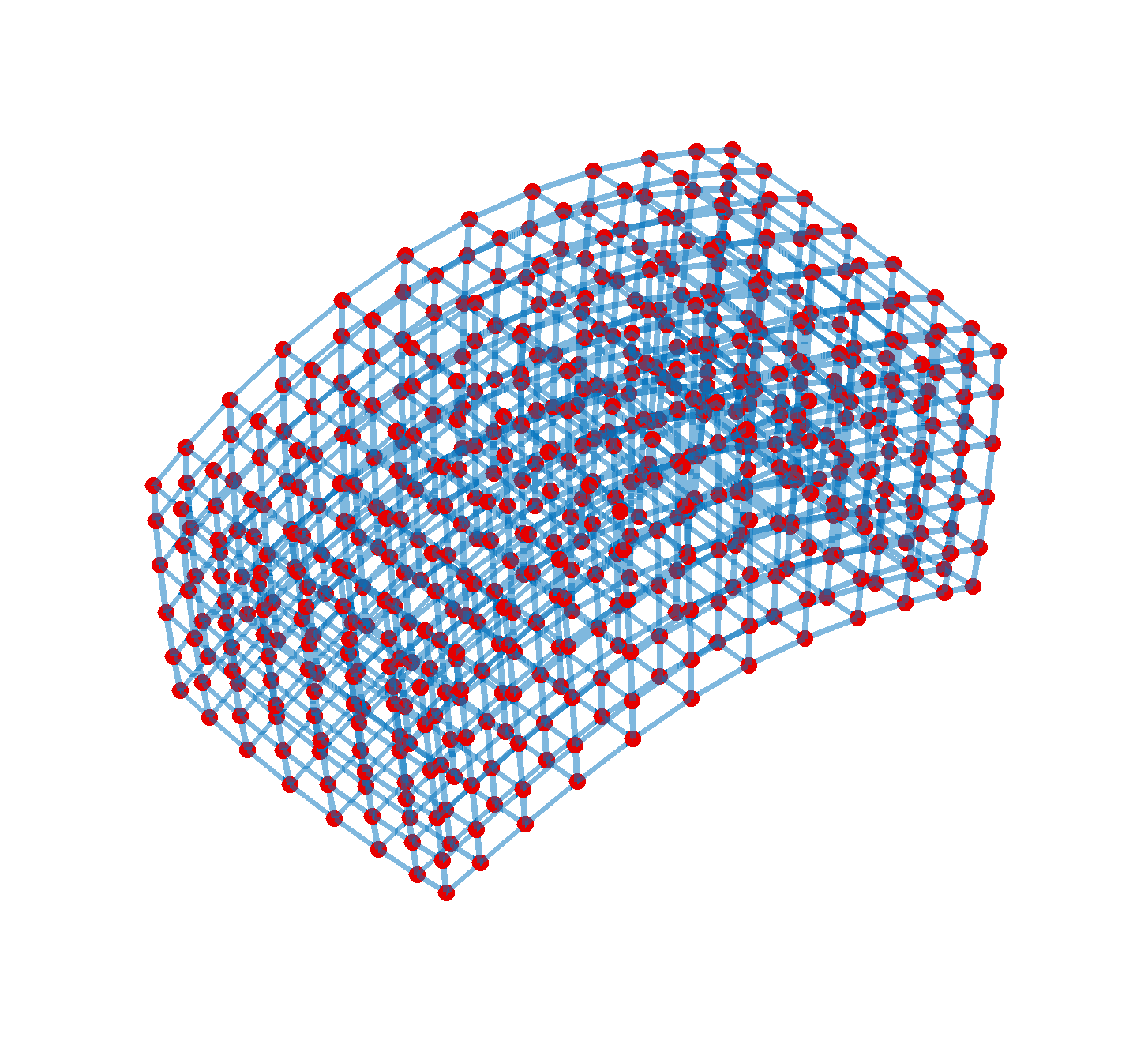
An example of using the above to make a 12 x 8 x 6 lattice is
L = LATTICE([12,8,6])
and plotting it
plot(graph(L),"Layout", "force3")
gives us this pretty beast:
![enter image description here]() (After some cosmetic tweaks, of course.)
(After some cosmetic tweaks, of course.)
Hopefully you found this response both useful and enjoyable to read.
Cheers!