(Because it was unclear in the original version of the question whether you meant to remove a subsequence or an unordered list, I've updated my answer to address both cases.)
1. Removing a sub-sequence in order
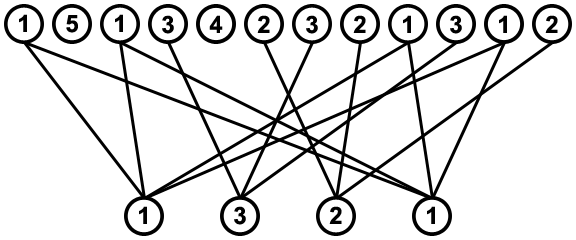
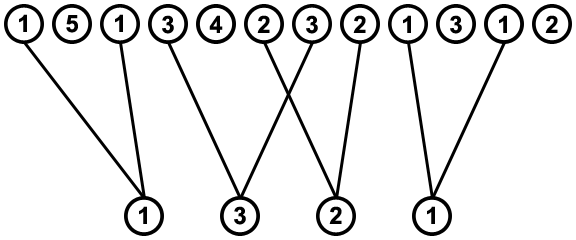
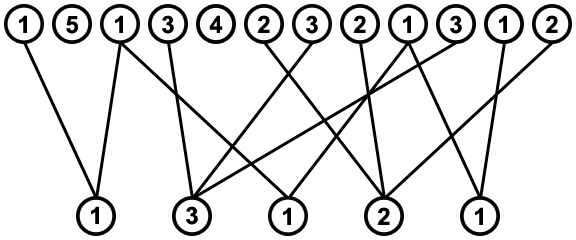
We get a sequence of values, e.g. [1,5,1,3,4,2,3,2,1,3,1,2], and a sub-sequence of values to be removed from the first sequence, e.g. [1,3,2,1]. If we find where every instance of the values is situated in the sequence, we get a graph like this:
![all connections]()
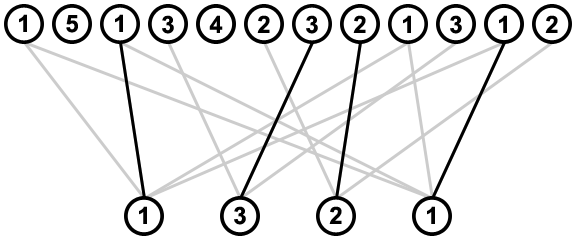
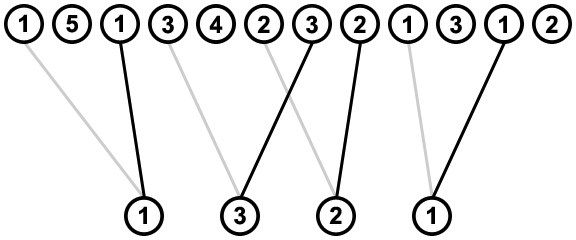
Finding all ways in which the values can be removed from the sequence, in order, then means finding all ways in which the to-be-removed values in the bottom row can be connected to an instance in the sequence, without any lines crossing, e.g.:
![example solution]()
To avoid removing values in a way which doesn't lead to a valid solution (e.g. starting by removing the right-most value 1, after which there is no value 3 that can be removed) we will first remove all the connections in the graph that lead to such invalid solutions.
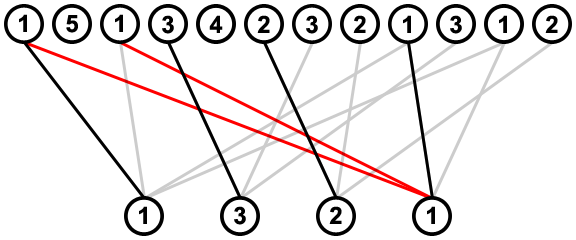
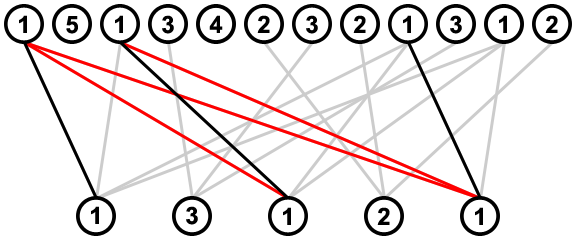
This will be done by iterating over the sub-sequence twice. First we do this left-to-right, and for each value, we look at its left-most connection, and remove any connections from the value to its right which meet or cross that connection; e.g. when considering the left-most connection from the value 2, two connections from the value 1 on its right (indicated in red) are removed because they cross this connection:
![removing crossed connections ltr]()
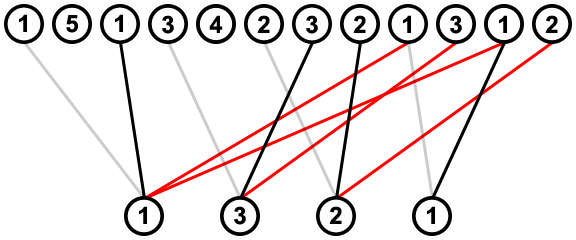
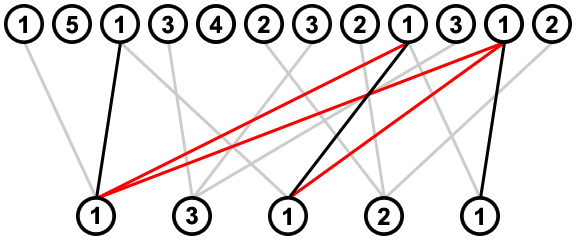
In the next step we go from right to left, and for each value, we look at its right-most connection, and remove any connections from the value on its left which meet or cross that connection; e.g. when considering the right-most connection from the value 1 on the right, the right-most connection from the value 2 on its left (indicated in red) is removed because it crosses this connection:
![removing crossed connections rtl]()
We then end up with the simplified graph shown below. The combinations are then made by combining every connected instance of each value in the sub-sequence, using e.g. recursion: you iterate over the options for the first value in the sub-sequence, and each time recurse with the rest of the sub-sequence, so that the option for the first value is combined with all the options for the other values.
![simplified graph]()
There can be crossed connections in the simplified graph, but these are no longer problematic. In the example you'll see that even if the right connection is chosen for the value 3, there is a connection for the value 2 which doesn't cross with it:
![example solution in simplified graph]()
Turning this into code is relatively straightforward; below the code snippet you will find a run-through of the code with the data from the example.
function removeSubSeq(seq, sub) {
var posi = []; // list position of values in seq, then connect to positions in sub
sub.forEach(function(elem) {posi[elem] = []});
seq.forEach(function(elem, index) {if (posi[elem]) posi[elem].push(index)});
var conn = sub.map(function(elem) {return posi[elem].slice()});
for (var i = 1; i < conn.length; i++) {
var left = conn[i - 1][0];
while (conn[i][0] <= left) {
conn[i].shift(); // remove crossed connection left-to-right
}
}
for (var i = conn.length - 2; i >= 0; i--) {
var right = conn[i + 1][conn[i + 1].length - 1];
while (conn[i][conn[i].length - 1] >= right) {
conn[i].pop(); // remove crossed connection right-to-left
}
}
var combinations = [], result = [];
combine(0, -1, []); // initiate recursion to find combinations
for (var i = 0; i < combinations.length; i++) {
result[i] = seq.slice(); // create copies of seq and remove values
for (var j = combinations[i].length - 1; j >= 0; j--) {
result[i].splice(combinations[i][j], 1);
}
}
return result;
function combine(step, prev, comb) { // generate combinations using recursion
for (var i = 0; i < conn[step].length; i++) {
var curr = conn[step][i];
if (prev >= curr) continue; // skip crossed connection
if (step + 1 == conn.length) combinations.push(comb.concat([curr]));
else combine(step + 1, curr, comb.concat([curr]));
}
}
}
var result = removeSubSeq([1,5,1,3,4,2,3,2,1,3,1,2], [1,3,2,1]);
for (var i in result) document.write(result[i] + "<br>");
The code performs these steps:
- Create an associative array of the position of instances of each value present in sub:
posi[1] = [0,2,8,10], posi[2] = [5,7,11], posi[3] = [3,6,9]}
- Create a 2D array which links the positions in the sub-sequence to those in the sequence:
conn = [[0,2,8,10],[3,6,9],[5,7,11],[0,2,8,10]]
- Go over the array left-to-right and remove crossed connections:
conn = [[0,2,8,10],[3,6,9],[5,7,11],[8,10]]
- Go over the array right-to-left and remove crossed connections:
conn = [[0,2],[3,6],[5,7],[8,10]]
- Generate all combinations of the positions using recursion:
combinations = [[0,3,5,8],[0,3,5,10],[0,3,7,8],[0,3,7,10],
[0,6,7,8],[0,6,7,10],[2,3,5,8],[2,3,5,10],
[2,3,7,8],[2,3,7,10],[2,6,7,8],[2,6,7,10]]
- Use the combinations to remove the values from copies of the sequence (see Code Snippet output).
2. Removing an unordered list of values
If the list of values to be removed is not necessarily a sub-sequence of the main sequence, and the values can be removed in any order, the same method as above can be used, with a relaxation of the crossed connection rules:
Removing crossed connections from the position list, and avoiding crossed connections when generating the combinations, only has to be done for identical values.
In this example, only the crossed connections for the duplicate values 1 are removed; first left-to-right:
![removing crossed connections ltr]()
and then right-to-left:
![removing crossed connections rtl]()
resulting in this simplified graph, with the problematic crossed connections for value 1 removed, and the crossed connections for values 2 and 3 remaining:
![simplified graph]()
Below is a code example adapted from the version for sub-sequences; only a few lines in the code are changed, as indicated with comments (and I also used a different method to remove the values from the sequence). The list of values to-be-removed is sorted at the start, so that identical values are grouped together, to make it easy to keep track of identical values.
function removeSubList(seq, sub) {
sub.sort(function(a, b) {return a - b}); /* SORT SUB-LIST FIRST */
var posi = []; // list position of values in seq, then connect to positions in sub
sub.forEach(function(elem) {posi[elem] = []});
seq.forEach(function(elem, index) {if (posi[elem]) posi[elem].push(index)});
var conn = sub.map(function(elem) {return posi[elem].slice()});
for (var i = 1; i < conn.length; i++) {
if (sub[i - 1] != sub[i]) continue; /* SKIP FOR NON-IDENTICAL VALUES */
var left = conn[i - 1][0];
while (conn[i][0] <= left) {
conn[i].shift(); // remove crossed connection left-to-right
}
}
for (var i = conn.length - 2; i >= 0; i--) {
if (sub[i] != sub[i + 1]) continue; /* SKIP FOR NON-IDENTICAL VALUES */
var right = conn[i + 1][conn[i + 1].length - 1];
while (conn[i][conn[i].length - 1] >= right) {
conn[i].pop(); // remove crossed connection right-to-left
}
}
var combinations = [], result = [];
combine(0, -1, []); // initiate recursion to find combinations
for (var i = 0; i < combinations.length; i++) {
var s = seq.slice(); // create copy of seq and delete values
combinations[i].forEach(function(elem) {delete s[elem]});
result[i] = s.filter(function(elem) {return elem != undefined});
}
return result;
function combine(step, prev, comb) { // generate combinations using recursion
for (var i = 0; i < conn[step].length; i++) {
var curr = conn[step][i];
if (prev >= curr && seq[prev] == seq[curr]) continue; /* SKIP FOR NIV */
if (step + 1 == conn.length) combinations.push(comb.concat([curr]));
else combine(step + 1, curr, comb.concat([curr]));
}
}
}
var result = removeSubList([1,5,1,3,4,2,3,2,1,3,1,2], [1,3,1,2,1]);
for (var i in result) document.write(result[i] + "<br>");