Can anybody explain me the numpy.indices()?

Question

I've read documentation several times about np.indices() but I can't seem to grasp what is it about. I've used it numerous times on things to see what it does, but I still can't really get it. Maybe the thing is I'm a beginner in programming so I can't understand the idea behind the words describing it. In addition I'm not a native English speaker (though I have no problems with it). I would be very grateful for kind of easier explanation, possibly on some example. Thanks.

Pons

Don't say you're a begineer, I've learned numpy many years, also confused on this indices() function. Thanks for your asking this question. – Duster

Answer 1

Suppose you have a matrix M whose (i,j)-th element equals

M_ij = 2*i + 3*j

One way to define this matrix would be

i, j = np.indices((2,3))
M = 2*i + 3*j

which yields

array([[0, 3, 6],
       [2, 5, 8]])

In other words, np.indices returns arrays which can be used as indices. The elements in i indicate the row index:

In [12]: i
Out[12]: 
array([[0, 0, 0],
       [1, 1, 1]])

The elements in j indicate the column index:

In [13]: j
Out[13]: 
array([[0, 1, 2],
       [0, 1, 2]])

Clea

The documentation has been carefully written so as to effectively mask this fact. – Pourboire

Answer 2

The already posted answers are still complex so here is the simplest way to understand this.

---

Step 1: Let's create a 2x2 grid

ids = np.indices((2,2))

Step 2: Now let's unpack the i,j indices

i, j = ids 

These are the indices i,j:

print(i)
[[0 0]
 [1 1]]

print(j)
[[0 1]
 [0 1]]

Step 3: Understand what i,j represent

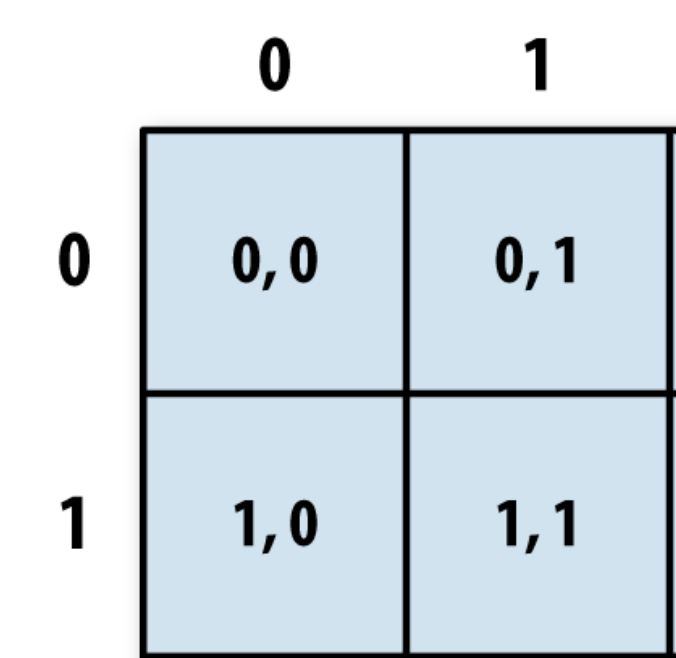
The easy way to think of it is to make pairs as (i0,j0), (i1,j1), (i2,j2), (i3,j3) i.e. match each element of i with the corresponding element of j.

So we get: (0,0), (0,1), (1,0), (1,1).

These are exactly the indices of a 2x2 grid:

Miliary

Answer 3

I've understood with this code.

The following function has the same behavior as np.indices().

# fixed dimensions=(2,3,4)
def my_indices():
    dimensions = (2,3,4)
    A = np.empty(dimensions)
    # dimensions[0] = 2
    A[0, :, :] = 0
    A[1, :, :] = 1

    B = np.empty(dimensions)
    # dimensions[1] = 3
    B[:, 0, :] = 0
    B[:, 1, :] = 1
    B[:, 2, :] = 2

    C = np.empty(dimensions)
    # dimensions[2] = 4
    C[:, :, 0] = 0
    C[:, :, 1] = 1
    C[:, :, 2] = 2
    C[:, :, 3] = 3

    return [A, B, C] 

Call

A, B, C = my_indices()
print(A.shape)
print(B.shape)
print(C.shape)
print('A\n', A)
print('B\n', B)
print('C\n', C)

RESULT

(2, 3, 4)
(2, 3, 4)
(2, 3, 4)
A
 [[[0. 0. 0. 0.]
  [0. 0. 0. 0.]
  [0. 0. 0. 0.]]

 [[1. 1. 1. 1.]
  [1. 1. 1. 1.]
  [1. 1. 1. 1.]]]

B
 [[[0. 0. 0. 0.]
  [1. 1. 1. 1.]
  [2. 2. 2. 2.]]

 [[0. 0. 0. 0.]
  [1. 1. 1. 1.]
  [2. 2. 2. 2.]]]

C
 [[[0. 1. 2. 3.]
  [0. 1. 2. 3.]
  [0. 1. 2. 3.]]

 [[0. 1. 2. 3.]
  [0. 1. 2. 3.]
  [0. 1. 2. 3.]]]

np.indices() use case

def create_hsv_map():
    img_hsv = np.empty((180, 256, 3), np.uint8)
    hue, saturation = np.indices((180,256))
    img_hsv[:, :, 0] = hue
    img_hsv[:, :, 1] = saturation
    img_hsv[:, :, 2] = 255
    # ...

example with np.repeat() instead of np.indices()

def create_hsv_map2():
    img_hsv = np.empty((180, 256, 3), np.uint8)
    hue = np.repeat(np.arange(180).reshape(180, 1), repeats=256, axis=1)
    saturation = np.repeat(np.arange(256).reshape(1, 256), repeats=180, axis=0)
    img_hsv[:, :, 0] = hue
    img_hsv[:, :, 1] = saturation
    img_hsv[:, :, 2] = 255
    # ...

Attend