How do I iterate through two lists in parallel?

Question

I have two iterables, and I want to go over them in pairs:

foo = [1, 2, 3]
bar = [4, 5, 6]

for (f, b) in iterate_together(foo, bar):
    print("f:", f, " |  b:", b)

That should result in:

f: 1  |  b: 4
f: 2  |  b: 5
f: 3  |  b: 6

One way to do it is to iterate over the indices:

for i in range(len(foo)):
    print("f:", foo[i], " |  b:", bar[i])

But that seems somewhat unpythonic to me. Is there a better way to do it?

---

<sub>Related tasks:
* How to merge lists into a list of tuples? - given the above foo and bar, create the list [(1, 4), (2, 5), (3, 6)].
* How can I make a dictionary (dict) from separate lists of keys and values? - create the dict {1: 4, 2: 5, 3: 6}.
* Create a dictionary with comprehension - constructing dict using zip in a dict comprehension.</sub>

Pederast

Answer 1

Python 3

for f, b in zip(foo, bar):
    print(f, b)

zip stops when the shorter of foo or bar stops.

In Python 3, zip returns an iterator of tuples, like itertools.izip in Python2. To get a list of tuples, use list(zip(foo, bar)). And to zip until both iterators are exhausted, you would use itertools.zip_longest.

Python 2

In Python 2, zip returns a list of tuples. This is fine when foo and bar are not massive. If they are both massive then forming zip(foo,bar) is an unnecessarily massive temporary variable, and should be replaced by itertools.izip or itertools.izip_longest, which returns an iterator instead of a list.

import itertools
for f,b in itertools.izip(foo,bar):
    print(f,b)
for f,b in itertools.izip_longest(foo,bar):
    print(f,b)

izip stops when either foo or bar is exhausted. izip_longest stops when both foo and bar are exhausted. When the shorter iterator(s) are exhausted, izip_longest yields a tuple with None in the position corresponding to that iterator. You can also set a different fillvalue besides None if you wish. See here for the full story.

---

Note also that zip and its zip-like brethen can accept an arbitrary number of iterables as arguments. For example,

for num, cheese, color in zip([1,2,3], ['manchego', 'stilton', 'brie'], 
                              ['red', 'blue', 'green']):
    print('{} {} {}'.format(num, color, cheese))

prints

1 red manchego
2 blue stilton
3 green brie

Lewes

Usually in Python, simpler is faster. In CPython, zip's for-loop and item-getting is implemented in C. In contrast, [(x[i], y[i]) for i in range(...)] uses a Python-level for-loop and each x[i] or y[i] requires a Python-level call to __getitem__. Generally, C-loops beat Python loops and fewer function calls is faster than more function calls. So intuition points to zip being faster than indexing. – Lewes

Of course, blanket statements about performance are foolish. So it's good to get familiar with timeit and test things for yourself. A little timeit test on my machine confirms list(zip(x,y)) is about 3x faster than [(x[i], y[i]) for i in range(1000)] for x = y = list(range(1000)). – Lewes

urr...doesn't zip need the lists to be equal? – Baguette

@AbhishekRai only with strict=True – Unbuild

Answer 2

You want the zip function.

for (f,b) in zip(foo, bar):
    print "f: ", f ,"; b: ", b

Nicolais

Answer 3

Building on the answer by @unutbu, I have compared the iteration performance of two identical lists when using Python 3.6's zip() functions, Python's enumerate() function, using a manual counter (see count() function), using an index-list, and during a special scenario where the elements of one of the two lists (either foo or bar) may be used to index the other list. Their performances for printing and creating a new list, respectively, were investigated using the timeit() function where the number of repetitions used was 1000 times. One of the Python scripts that I had created to perform these investigations is given below. The sizes of the foo and bar lists had ranged from 10 to 1,000,000 elements.

Results:

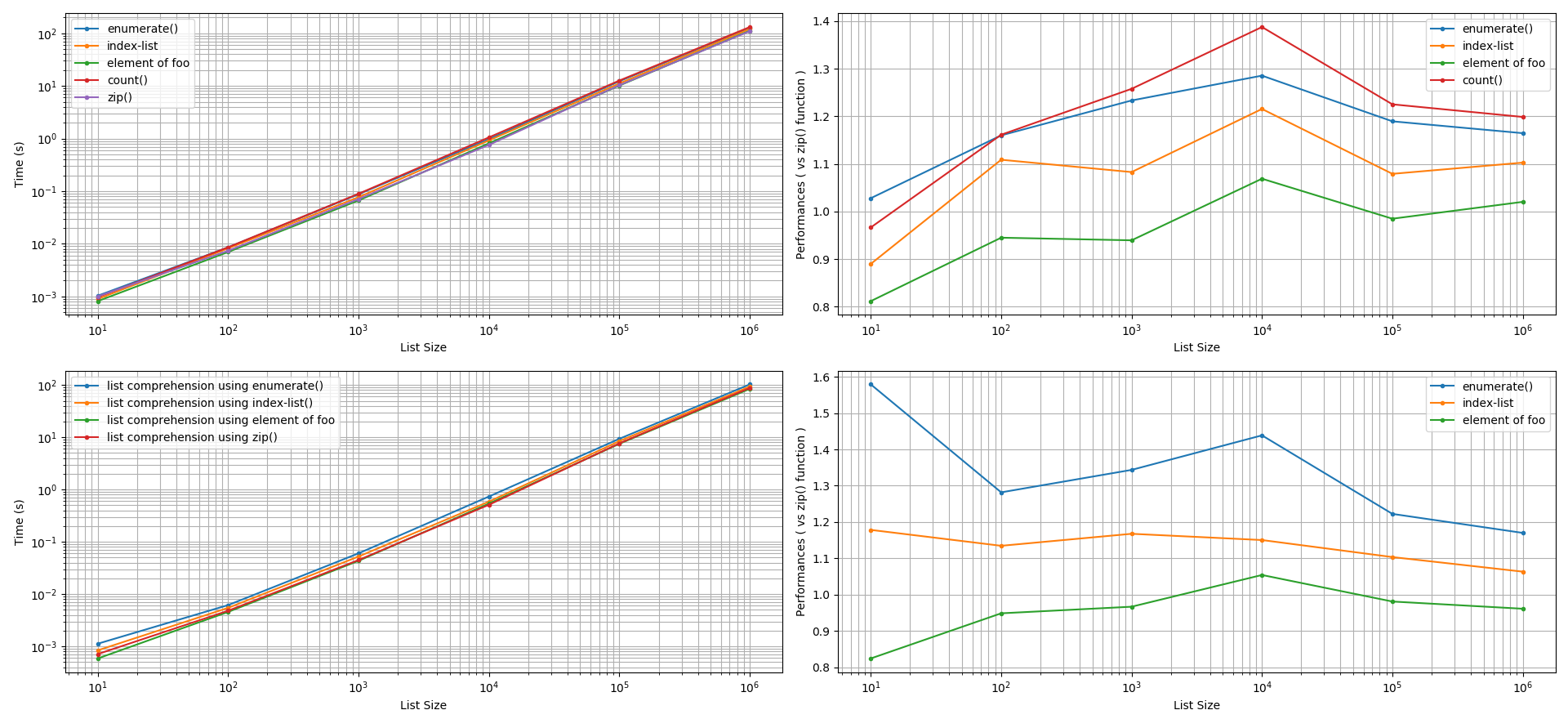
1. For printing purposes: The performances of all the considered approaches were observed to be approximately similar to the zip() function, after factoring an accuracy tolerance of +/-5%. An exception occurred when the list size was smaller than 100 elements. In such a scenario, the index-list method was slightly slower than the zip() function while the enumerate() function was ~9% faster. The other methods yielded similar performance to the zip() function.

2. For creating lists: Two types of list creation approaches were explored: using the (a) list.append() method and (b) list comprehension. After factoring an accuracy tolerance of +/-5%, for both of these approaches, the zip() function was found to perform faster than the enumerate() function, than using a list-index, than using a manual counter. The performance gain by the zip() function in these comparisons can be 5% to 60% faster. Interestingly, using the element of foo to index bar can yield equivalent or faster performances (5% to 20%) than the zip() function.

Making sense of these results:

A programmer has to determine the amount of compute-time per operation that is meaningful or that is of significance.

For example, for printing purposes, if this time criterion is 1 second, i.e. 10**0 sec, then looking at the y-axis of the graph that is on the left at 1 sec and projecting it horizontally until it reaches the monomials curves, we see that lists sizes that are more than 144 elements will incur significant compute cost and significance to the programmer. That is, any performance gained by the approaches mentioned in this investigation for smaller list sizes will be insignificant to the programmer. The programmer will conclude that the performance of the zip() function to iterate print statements is similar to the other approaches.

Conclusion

Notable performance can be gained from using the zip() function to iterate through two lists in parallel during list creation. When iterating through two lists in parallel to print out the elements of the two lists, the zip() function will yield similar performance as the enumerate() function, as to using a manual counter variable, as to using an index-list, and as to during the special scenario where the elements of one of the two lists (either foo or bar) may be used to index the other list.

The Python 3.6 script that was used to investigate list creation.

import timeit
import matplotlib.pyplot as plt
import numpy as np


def test_zip( foo, bar ):
    store = []
    for f, b in zip(foo, bar):
        #print(f, b)
        store.append( (f, b) )

def test_enumerate( foo, bar ):
    store = []
    for n, f in enumerate( foo ):
        #print(f, bar[n])
        store.append( (f, bar[n]) )

def test_count( foo, bar ):
    store = []
    count = 0
    for f in foo:
        #print(f, bar[count])
        store.append( (f, bar[count]) )
        count += 1

def test_indices( foo, bar, indices ):
    store = []
    for i in indices:
        #print(foo[i], bar[i])
        store.append( (foo[i], bar[i]) )

def test_existing_list_indices( foo, bar ):
    store = []
    for f in foo:
        #print(f, bar[f])
        store.append( (f, bar[f]) )


list_sizes = [ 10, 100, 1000, 10000, 100000, 1000000 ]
tz = []
te = []
tc = []
ti = []
tii= []

tcz = []
tce = []
tci = []
tcii= []

for a in list_sizes:
    foo = [ i for i in range(a) ]
    bar = [ i for i in range(a) ]
    indices = [ i for i in range(a) ]
    reps = 1000

    tz.append( timeit.timeit( 'test_zip( foo, bar )',
                              'from __main__ import test_zip, foo, bar',
                              number=reps
                              )
               )
    te.append( timeit.timeit( 'test_enumerate( foo, bar )',
                              'from __main__ import test_enumerate, foo, bar',
                              number=reps
                              )
               )
    tc.append( timeit.timeit( 'test_count( foo, bar )',
                              'from __main__ import test_count, foo, bar',
                              number=reps
                              )
               )
    ti.append( timeit.timeit( 'test_indices( foo, bar, indices )',
                              'from __main__ import test_indices, foo, bar, indices',
                              number=reps
                              )
               )
    tii.append( timeit.timeit( 'test_existing_list_indices( foo, bar )',
                               'from __main__ import test_existing_list_indices, foo, bar',
                               number=reps
                               )
                )

    tcz.append( timeit.timeit( '[(f, b) for f, b in zip(foo, bar)]',
                               'from __main__ import foo, bar',
                               number=reps
                               )
                )
    tce.append( timeit.timeit( '[(f, bar[n]) for n, f in enumerate( foo )]',
                               'from __main__ import foo, bar',
                               number=reps
                               )
                )
    tci.append( timeit.timeit( '[(foo[i], bar[i]) for i in indices ]',
                               'from __main__ import foo, bar, indices',
                               number=reps
                               )
                )
    tcii.append( timeit.timeit( '[(f, bar[f]) for f in foo ]',
                                'from __main__ import foo, bar',
                                number=reps
                                )
                 )

print( f'te  = {te}' )
print( f'ti  = {ti}' )
print( f'tii = {tii}' )
print( f'tc  = {tc}' )
print( f'tz  = {tz}' )

print( f'tce  = {te}' )
print( f'tci  = {ti}' )
print( f'tcii = {tii}' )
print( f'tcz  = {tz}' )

fig, ax = plt.subplots( 2, 2 )
ax[0,0].plot( list_sizes, te, label='enumerate()', marker='.' )
ax[0,0].plot( list_sizes, ti, label='index-list', marker='.' )
ax[0,0].plot( list_sizes, tii, label='element of foo', marker='.' )
ax[0,0].plot( list_sizes, tc, label='count()', marker='.' )
ax[0,0].plot( list_sizes, tz, label='zip()', marker='.')
ax[0,0].set_xscale('log')
ax[0,0].set_yscale('log')
ax[0,0].set_xlabel('List Size')
ax[0,0].set_ylabel('Time (s)')
ax[0,0].legend()
ax[0,0].grid( b=True, which='major', axis='both')
ax[0,0].grid( b=True, which='minor', axis='both')

ax[0,1].plot( list_sizes, np.array(te)/np.array(tz), label='enumerate()', marker='.' )
ax[0,1].plot( list_sizes, np.array(ti)/np.array(tz), label='index-list', marker='.' )
ax[0,1].plot( list_sizes, np.array(tii)/np.array(tz), label='element of foo', marker='.' )
ax[0,1].plot( list_sizes, np.array(tc)/np.array(tz), label='count()', marker='.' )
ax[0,1].set_xscale('log')
ax[0,1].set_xlabel('List Size')
ax[0,1].set_ylabel('Performances ( vs zip() function )')
ax[0,1].legend()
ax[0,1].grid( b=True, which='major', axis='both')
ax[0,1].grid( b=True, which='minor', axis='both')

ax[1,0].plot( list_sizes, tce, label='list comprehension using enumerate()',  marker='.')
ax[1,0].plot( list_sizes, tci, label='list comprehension using index-list()',  marker='.')
ax[1,0].plot( list_sizes, tcii, label='list comprehension using element of foo',  marker='.')
ax[1,0].plot( list_sizes, tcz, label='list comprehension using zip()',  marker='.')
ax[1,0].set_xscale('log')
ax[1,0].set_yscale('log')
ax[1,0].set_xlabel('List Size')
ax[1,0].set_ylabel('Time (s)')
ax[1,0].legend()
ax[1,0].grid( b=True, which='major', axis='both')
ax[1,0].grid( b=True, which='minor', axis='both')

ax[1,1].plot( list_sizes, np.array(tce)/np.array(tcz), label='enumerate()', marker='.' )
ax[1,1].plot( list_sizes, np.array(tci)/np.array(tcz), label='index-list', marker='.' )
ax[1,1].plot( list_sizes, np.array(tcii)/np.array(tcz), label='element of foo', marker='.' )
ax[1,1].set_xscale('log')
ax[1,1].set_xlabel('List Size')
ax[1,1].set_ylabel('Performances ( vs zip() function )')
ax[1,1].legend()
ax[1,1].grid( b=True, which='major', axis='both')
ax[1,1].grid( b=True, which='minor', axis='both')

plt.show()

Gumm

Answer 4

You should use 'zip' function. Here is an example how your own zip function can look like

def custom_zip(seq1, seq2):
    it1 = iter(seq1)
    it2 = iter(seq2)
    while True:
        yield next(it1), next(it2)

Eulau

This is a pretty limited reinvention of zip and the wording is rather misleading. If you're going to reinvent the wheel (don't--it's a builtin function, not a dependency), at least this answer accepts a variable number of iterables and generally behaves as you'd expect zip to. – Gilletta

Answer 5

Here's how to do it with a list comprehension:

a = (1, 2, 3)
b = (4, 5, 6)
[print('f:', i, '; b', j) for i, j in zip(a, b)]

It prints:

f: 1 ; b 4
f: 2 ; b 5
f: 3 ; b 6

Lilalilac

Is it Pythonic to use list comprehensions for just side effects? – Toneme

Answer 6

You can bundle the nth elements into a tuple or list using comprehension, then pass them out with a generator function.

def iterate_multi(*lists):
    for i in range(min(map(len,lists))):
        yield tuple(l[i] for l in lists)

for l1, l2, l3 in iterate_multi([1,2,3],[4,5,6],[7,8,9]):
    print(str(l1)+","+str(l2)+","+str(l3))

Ahmadahmar

Answer 7

We can just use an index to iterate...

foo = ['a', 'b', 'c']
bar = [10, 20, 30]
for indx, itm in enumerate(foo):
    print (foo[indx], bar[indx])

Hebbel

Why use enumerate if you're not actually using itm? Either change to print(itm, bar[index]) or simply loop as for indx in range(len(foo)) – Mojica

Answer 8

If you want to keep the indices while using zip() to iterate through multiple lists together, you can pass the zip object to enumerate():

for i, (f, b) in enumerate(zip(foo, bar)):
    # do something

e.g. if you want to print out the positions where the values differ in 2 lists, you can do so as follows.

foo, bar = ['a', 'b', 'c'], ['a', 'a', 'c']

for i, (f, b) in enumerate(zip(foo, bar)):
    if f != b:
        print(f"items at index {i} are different")
    
# items at index 1 are different

---

If your lists don't have the same length, then zip() iterates until the shortest list ends. If you want to iterate until the longest list ends, use zip_longest from the built-in itertools module. It pads the missing values by None by default (but you can change it to any value you want with the fillvalue parameter).

from itertools import zip_longest
for f, b in zip_longest(foo, bar):
    # do something

Katzen

Answer 9

The most efficient way is the old way.

import time

abc = list(range(10000000))
xyz = list(range(10000000))
start = time.time_ns()
for i in range(0, (len(abc)-1)):
    print("{} and {}".format(abc[i], xyz[i]))
print("Total time: {}".format(time.time_ns()-start))

Time: 12315440476ns

import time

abc = list(range(10000000))
xyz = list(range(10000000))
start = time.time_ns()
for a, b in zip(abc, xyz):
    print("{} and {}".format(a, b))
print("Total time: {}".format(time.time_ns()-start))

Time: 12338617143ns

Xenophobia