Extract street network from a raster image

Question

I have a 512x512 image of a street grid:

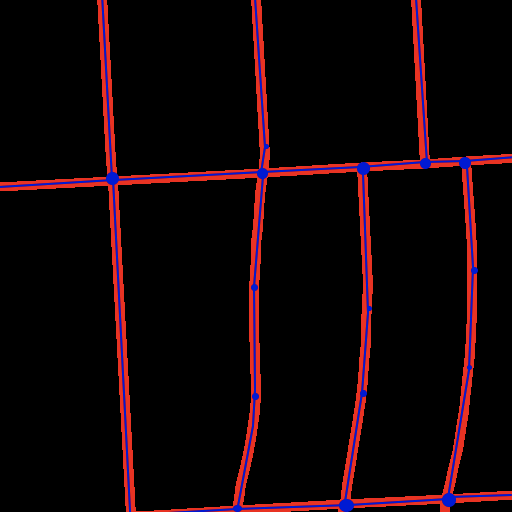
I'd like to extract polylines for each of the streets in this image (large blue dots = intersections, small blue dots = points along polylines):

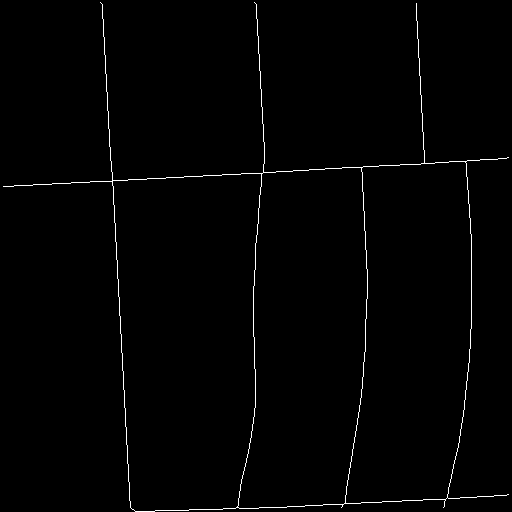
I've tried a few techniques! One idea was to start with skeletonize to compress the streets down to 1px wide lines:

from skimage import morphology
morphology.skeletonize(streets_data))

Unfortunately this has some gaps that break the connectivity of the street network; I'm not entirely sure why, but my guess is that this is because some of the streets are 1px narrower in some places and 1px wider in others. (update: the gaps aren't real; they're entirely artifacts of how I was displaying the skeleton. See this comment for the sad tale. The skeleton is well-connected.)

I can patch these using a binary_dilation, at the cost of making the streets somewhat variable width again:

out = morphology.skeletonize(streets_data)
out = morphology.binary_dilation(out, morphology.selem.disk(1))

With a re-connected grid, I can run the Hough transform to find line segments:

import cv2
rho = 1  # distance resolution in pixels of the Hough grid
theta = np.pi / 180  # angular resolution in radians of the Hough grid
threshold = 8  # minimum number of votes (intersections in Hough grid cell)
min_line_length = 10  # minimum number of pixels making up a line
max_line_gap = 2  # maximum gap in pixels between connectable line segments

# Run Hough on edge detected image
# Output "lines" is an array containing endpoints of detected line segments
lines = cv2.HoughLinesP(
    out, rho, theta, threshold, np.array([]),
    min_line_length, max_line_gap
)

line_image = streets_data.copy()
for i, line in enumerate(lines):
    for x1,y1,x2,y2 in line:
        cv2.line(line_image,(x1,y1),(x2,y2), 2, 1)

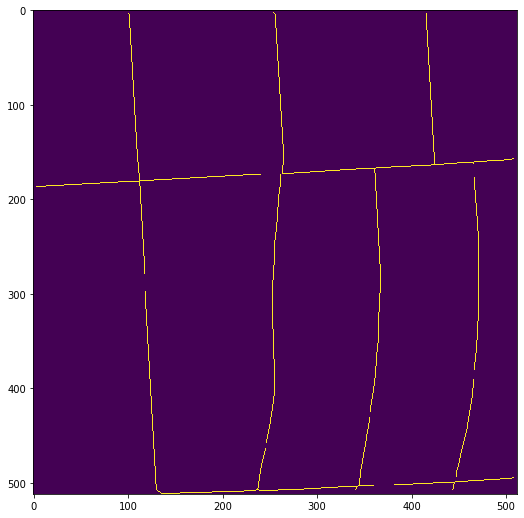
This produces a whole jumble of overlapping line segments, along with some gaps (look at the T intersection on the right side):

At this point I could try to de-dupe overlapping line segments, but it's not really clear to me that this is a path towards a solution, especially given that gap.

Are there more direct methods available to get at the network of polylines I'm looking for? In particular, what are some methods for:

1. Finding the intersections (both four-way and T intersections).
2. Shrinking the streets to all be 1px wide, allowing that there may be some variable width.
3. Finding the polylines between intersections.

Annecorinne

You could give this a try. – Carlyn

Answer 1

If you want to improve your "skeletonization", you could try the following algorithm to obtain the "1-px wide streets":

import imageio
import numpy as np
from matplotlib import pyplot as plt
from scipy.ndimage import distance_transform_edt
from skimage.segmentation import watershed

# read image
image_rgb = imageio.imread('1mYBD.png')

# convert to binary
image_bin = np.max(image_rgb, axis=2) > 0

# compute the distance transform (only > 0)
distance = distance_transform_edt(image_bin)

# segment the image into "cells" (i.e. the reciprocal of the network)
cells = watershed(distance)

# compute the image gradients
grad_v = np.pad(cells[1:, :] - cells[:-1, :], ((0, 1), (0, 0)))
grad_h = np.pad(cells[:, 1:] - cells[:, :-1], ((0, 0), (0, 1)))

# given that the cells have a constant value,
# only the edges will have non-zero gradient
edges = (abs(grad_v) > 0) + (abs(grad_h) > 0)

# extract points into (x, y) coordinate pairs
pos_v, pos_h = np.nonzero(edges)

# display points on top of image
plt.imshow(image_bin, cmap='gray_r')
plt.scatter(pos_h, pos_v, 1, np.arange(pos_h.size), cmap='Spectral')

The algorithm works on the "blocks" rather than the "streets", take a look into the cells image:

Botchy

Using watershed to find the midpoints of the lines is plain brilliant. I guess this only identifies the precise midline if the cells are approximately the same size? Seems that way at the 3-way junctions. Still a worthy trade-off, IMO. – Systemize

I think this is independent of cell size. it should find the midlines within the gaps between cells. you could try an experiment on a hand-drawn input. – Magalimagallanes

Thanks for this! See the update to my question. Sadly the code I was using to display the skeleton had a bug that made it look like there were gaps, even though there were none. In reality the skeleton is connected. skimage.morphology.skeleton works a bit better than this approach because it doesn't require a "block" on either side of every street, e.g. for the street that trails off at the bottom center of the image in this answer. – Annecorinne

Answer 2

I was on the right track with skeleton; it does produce a connected, 1px wide version of the street grid. It's just that there was a bug in my display code (see this comment). Here's what the skeleton actually looks like:

from skimage import morphology
morphology.skeletonize(streets_data))

From here the reference to NEFI2 in RJ Adriaansen's comment was extremely helpful. I wasn't able to get an extraction pipeline to run on my image using their GUI, but I was able to cobble together something using their code and approach.

Here's the general procedure I wound up with:

• Find candidate nodes. These are pixels in the skeleton with either one neighbor (end of a line) or 3+ neighbors (an intersection). NEFI2 calls this the Zhang-Suen algorithm. For four-way intersections, it produces multiple nodes so we need to merge them.
• Repeat until no two nodes are too close together:
  • Use breadth-first search (flood fill) to connect nodes.
  • If two connected nodes are within D of each other, merge them.
• Run shapely's simplify on the paths between nodes to get polylines.

I put this all together in a repo here: extract-raster-network.

This works pretty well on my test images! Here are some sample images:

Annecorinne