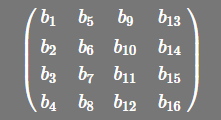Row-major vs Column-major confusion

Question

I've been reading a lot about this, the more I read the more confused I get.

My understanding: In row-major rows are stored contiguously in memory, in column-major columns are stored contiguously in memory. So if we have a sequence of numbers [1, ..., 9] and we want to store them in a row-major matrix, we get:

|1, 2, 3|
|4, 5, 6|
|7, 8, 9|

while the column-major (correct me if I'm wrong) is:

|1, 4, 7|
|2, 5, 8|
|3, 6, 9|

which is effectively the transpose of the previous matrix.

My confusion: Well, I don't see any difference. If we iterate on both the matrices (by rows in the first one, and by columns in the second one) we'll cover the same values in the same order: 1, 2, 3, ..., 9

Even matrix multiplication is the same, we take the first contiguous elements and multiply them with the second matrix columns. So say we have the matrix M:

|1, 0, 4| 
|5, 2, 7| 
|6, 0, 0|

If we multiply the previous row-major matrix R with M, that is R x M we'll get:

|1*1 + 2*0 + 3*4, 1*5 + 2*2 + 3*7, etc|
|etc.. |
|etc.. |

If we multiply the column-major matrix C with M, that is C x M by taking the columns of C instead of its rows, we get exactly the same result from R x M

I'm really confused, if everything is the same, why do these two terms even exist? I mean even in the first matrix R, I could look at the rows and consider them columns...

Am I missing something? What does row-major vs col-major actually imply on my matrix math? I've always learned in my Linear Algebra classes that we multiply rows from the first matrix with columns from the second one, does that change if the first matrix was in column-major? do we now have to multiply its columns with columns from the second matrix like I did in my example or was that just flat out wrong?

Any clarifications are really appreciated!

EDIT: One of the other main sources of confusion I'm having is GLM... So I hover over its matrix type and hit F12 to see how it's implemented, there I see a vector array, so if we have a 3x3 matrix we have an array of 3 vectors. Looking at the type of those vectors I saw 'col_type' so I assumed that each one of those vectors represent a column, and thus we have a column-major system right?

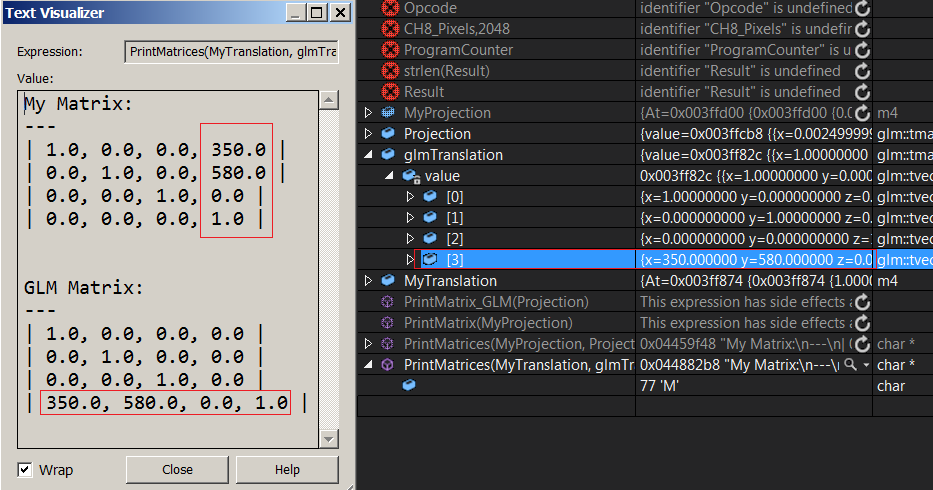
Well, I don't know to be honest. I wrote this print function to compare my translation matrix with glm's, I see the translation vector in glm at the last row, and mine is at the last column...

This adds nothing but more confusion. You can clearly see that each vector in glmTranslate matrix represents a row in the matrix. So... that means that the matrix is row-major right? What about my matrix? (I'm using a float array[16]) the translation values are in the last column, does that mean my matrix is column-major and I didn't now it? tries to stop head from spinning

Moneywort

Think of it as measuring in kilometers or miles. Both work fine, but if you get the two mixed up, you crash your lander on Mars. – Amboise

As far as I remember having a column major order layout in memory has great advantage utilizing the cache specially when used in tandem with SIMD vector instructions when you are performing block matrix multiplication, I'm surprised no one has brought that up in this SO. – Underpart

Answer 1

Let's look at algebra first; algebra doesn't even have a notion of "memory layout" and stuff.

From an algebraic pov, a MxN real matrix can act on a |R^N vector on its right side and yield a |R^M vector.

Thus, if you were sitting in an exam and given a MxN Matrix and a |R^N vector, you could with trivial operations multiply them and get a result - whether that result is right or wrong will not depend on whether the software your professor uses to check your results internally uses column-major or a row-major layout; it will only depend on if you calculated the contraction of each row of the matrix with the (single) column of the vector properly.

To produce a correct output, the software will - by whatever means - essentially have to contract each row of the Matrix with the column vector, just like you did in the exam.

---

Thus, the difference between software that aligns column-major and software that uses row-major-layout is not what it calculates, but just how.

To put it more pecisely, the difference between those layouts with regard to the topcial single row's contraction with the column vector is just the means to determine

Where is the next element of the current row?

• For a row-major-layout it's the element just in the next bucket in memory
• For a column-major-layout it's the element in the bucket M buckets away.

And thats it.

---

To show you how that column/row magic is summoned in practice:

You haven't tagged your question with "c++", but because you mentioned 'glm', I assume that you can get along with C++.

In C++'s standard library there's an infamous beast called valarray, which, besides other tricky features, has overloads of operator[], one of them can take a std::slice ( which is essentially a very boring thing, consisting of just three integer-type numbers).

This little slice thing however, has everything one would need to access a row-major-storage column-wise or a column-major-storage row-wise - it has a start, a length, and a stride - the latter represents the "distance to next bucket" I mentioned.

Intima

Thanks for the answer. What's making me confused is that picture I posted in my edit. The first matrix is a float4x4 array, the second is glm's which is an array of 4 vec4's. While glm is column major, looking at it in the debugger it looks like its row major (cause every vector seem to represent a row, at least visually)... why does it look that way? and what about my matrix? is it row or col major? – Moneywort

GLM and GLSL take four column vector and produce a field of 16 floats or doubles by copying the columns vectors in sequence into that field. If that flat field is viewed in a debugger and C-style shaped into a (4,4) shape, that indeed shows the columns of the matrix underlying storage as rows. – Intima

@Moneywort If you wanted to contract the top row of the matrix with a column vector to get the leading component of the result vector you would, given a flat field float M[16];, use M[0], M[1], M[2], M[3] of your matrix storage. GLM (and GLSL, and Fortran, and Blender...) would take M[0], M[4], M[8], M[12] of theirs - that's the difference in stride, which arises from different storage layout I had mentioned in my answer – Intima

Let me get this straight. 0- My matrix, is in row-major order because rows are stored contiguously in a flat array of floats correct? 1- GLM's matrix is column-major because they're using an array of vectors where each vector is a column, accessing those vectors == accessing the columns sequentially, correct?. 2- you said that row vs col is just a memory layout issue, and the math is still the same. Well, if I want to multiply my flat matrix with another 4x4 matrix, I would take the first row (which is contiguous) and multiply with elements of the first column in the second matrix, right? – Moneywort

(continuing) but when I want to multiply GLM's matrix by another matrix, we also take the first row and do the same math right? but the problem here is that row elements are not sequential in column-major, doesn't that mean that multiplication in this case is less efficient? (less cache coherency cause we're jumping a lot) – Moneywort

I guess what I'm trying to understand is: given 2 NxN matrices, we want to multiply them, do we take the first 'row' of the first matrix and multiply/add to the first column of the second matrix? OR take the first 'N' sequential elements of the first matrix and multiply those? – Moneywort

@Moneywort I understand I already did more than enough to help you master the difficulties you have with this topic, and you can answer your questions yourself if you carefully re-read my explanations. I do not intend to re-iterate what I already wrote.. – Intima

Answer 2

I think you are mixing up an implementation detail with usage, if you will.

Let's start with a two-dimensional array, or matrix:

    | 1  2  3 |
    | 4  5  6 |
    | 7  8  9 |

The problem is that computer memory is a one-dimensional array of bytes. To make our discussion easier, lets group the single bytes into groups of four, thus we have something looking like this, (each single, +-+ represents a byte, four bytes represents an integer value (assuming 32-bit operating systems) :

   -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-
    |       |       |       |       |       |       |       |       |  
   -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-
       \/                   \       /
      one byte               one integer

    low memory    ------>                          high memory

Another way of representing

So, the question is how to map a two dimensional structure (our matrix) onto this one dimensional structure (i.e. memory). There are two ways of doing this.

1. Row-major order: In this order we put the first row in memory first, and then the second, and so on. Doing this, we would have in memory the following:

    -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
     |   1   |   2   |   3   |   4   |   5   |   6   |   7   |   8   |   9   |
    -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
   

With this method, we can find a given element of our array by performing the following arithmetic. Suppose we want to access the $M_{ij}$ element of the array. If we assume that we have a pointer to the first element of the array, say ptr, and know the number of columns say nCol, we can find any element by:

     $M_{ij} = i*nCol + j$ 

To see how this works, consider M_{02} (i.e. first row, third column -- remember C is zero based.

      $M_{02} = 0*3 + 2 = 2

So we access the third element of the array.

2. Column-major ordering: In this order we put the first column in memory first, and then the second, and so or. Doing this we would have in memory the following:

    -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
     |   1   |   4   |   7   |   2   |   5   |   8   |   3   |   6   |   9   |
    -+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
   

So, the short answer - row-major and column-major format describe how the two (or higher) dimensional arrays are mapped into a one dimensional array of memory.

Secondrate

Thanks. But as a programmer what do I have to keep in mind when writing my own math libraries to use with OpenGL? How does row-major vs column-major affect the math operations on matrices (multiplication etc)? In other words: since OpenGL stores its matrices in column-major order, how does that affect (if at all) the way I handle matrix math? – Moneywort

row versus column is determined by language that you are using (for example C uses row-major form). All you need to be able to do is be able to figure out where in the one-dimensional array (i.e. memory) where the given array item is located. So for example, adding matrices A and B can be defined as $A + B = A_{ij} + B_{ij}$. If you are using row-major form, I showed how to convert a row-column location into an index, so if we assume we have a function int makeIndex(int row, int col) then the above matrix addition would be represented as A[makeIndex(i,j)] + B[makeIndex(i,j)] T. – Secondrate

@Secondrate I would disagree that major-ness is determined by language. It's determined function-by-function, I would say. Of course any decent matrix-math package will use the same convention throughout. I suppose Fortran and R and other math-centric languages which have matrices as primitive types would determine the in-memory convention. – Lyle

Answer 3

Doesn't matter what you use: just be consistent!

Row major or column major is just a convention. Doesn't matter. C uses row major, Fortran uses column. Both work. Use what's standard in your programming language/environment.

Mismatching the two will !@#$ stuff up

If you use row major addressing on a matrix stored in colum major, you can get the wrong element, read past end of the array, etc...

Row major: A(i,j) element is at A[j + i * n_columns];  <---- mixing these up will
Col major: A(i,j) element is at A[i + j * n_rows];     <---- make your code fubar

It's incorrect to say code to do matrix multiplication is the same for row major and column major

(Of course the math of matrix multiplication is the same.) Imagine you have two arrays in memory:

X = [x1, x2, x3, x4]    Y = [y1, y2, y3, y4]

If matrices are stored in column major then X, Y, and X*Y are:

IF COL MAJOR: [x1, x3  *  [y1, y3    =   [x1y1+x3y2, x1y3+x3y4
               x2, x4]     y2, y4]        x2y1+x4y2, x2y3+x4y4]

If matrices are stored in row major then X, Y, and X*Y are:

IF ROW MAJOR:  [x1, x2    [y1, y2     = [x1y1+x2y3, x1y2+x2y4;
                x3, x4]    y3, y4]       x3y1+x4y3, x3y2+x4y4];

X*Y in memory if COL major   [x1y1+x3y2, x2y1+x4y2, x1y3+x3y4, x2y3+x4y4]
              if ROW major   [x1y1+x2y3, x1y2+x2y4, x3y1+x4y3, x3y2+x4y4]

There's nothing deep going on here. It's just two different conventions. It's like measuring in miles or kilometers. Either works, you just can't flip back and forth between the two without converting!

Amboise

Thanks that's what I wanted to hear. Matrix math remain the same in the sense that we always take rows (not the first contiguous N elements) from the first matrix and multiply with columns from the second one. The only question I have left: If column elements are contiguous in memory in col-major, doesn't this mean that multiplying col-major matrices is less efficient than row-major ones? Because in our example: x1y1 + x3y2 well x1 and x3 are not contiguous (unlike x1,x2 in row-maj). In other words, we have to stride by '2' in col-maj to get the next element in the current row... – Moneywort

@Moneywort I don't know enough about CPU architecture and BLAS dgemm routines to know why, but I'm pretty confident this is not an issue. – Amboise

check out @YCJung answer. Iterating over a 2D array with the wrong stride could yield massive slow downs in performance. You could check out scott meyer's talk as well vimeo.com/97337258 – Moneywort

@Moneywort Yes, hitting cache is important, but how does that connect with row major vs. column major? With modern processors, modern linear algebra routines, etc... you'll have a hard finding a clear case where row-major vs. column-major will both (1) yield a meaningful difference in computation time and (2) you can predict which way it goes consistently ex-ante. Show some code that calls optimized BLAS/LAPACK routines where it actually matters. Maybe it happens, but good luck. IMHO, this is like arguing whether I will run a marathon faster if I shave off my left eyebrow vs. right eyebrow – Amboise

For what it's worth, "Doesn't matter what you use" is true mathematically but not from the perspective of performance. Column subsetting operations will be faster in column-major and row-subsetting operations will be faster in column-order. If you anticipate doing more of one than the other, than the choice of storage will affect performance, perhaps substantially. – Pergolesi

Answer 4

You are right. it doesn't matter if a system stored the data in a row-major structure or a column-major one. It is just like a protocol. Computer : "Hey, human. I'm going to store your array this way. No prob. Huh?" However, when it comes to performance, it matters. consider the following three things.

1. most arrays are accessed in row-major order.

2. When you access memory, it is not directly read from memory. You first store some blocks of data from memory to cache, then you read data from cache to your processor.

3. If the data you want does not exist in cache, cache should re-fetch the data from the memory

When a cache fetches data from memory, locality is important. That is, if you store data sparsely in memory, your cache should fetch data from memory more often. This action corrupts your programs performance because accessing memory is far slower(over 100times!) then accessing cache. The less you access memory, the faster your program. So, this row-major array is more efficient because accessing its data is more likely to be local.

Magavern

I would disagree with this. Yes accessing sparsed elements is bad. But from what I understood, in column-major the columns are stored contiguously just like the rows you're describing in the row-major configuration. So in both cases you're iterating sequentially over the elements with no cache hits. Unless you iterate a row-major matrix non-sequentially i.e. by M[Col][Row] instead of M[Row][Col] (i.e. iterating it vertically not horizontally) – Moneywort

I should have been clearer, when I said I disagree I was referring to "So, this row-major array is more efficient because accessing its data is more likely to be local" -- I agree with the rest but I don't see how it addresses my confusion. – Moneywort

@Moneywort You are right. If you are going to access the array column-major order and use the transposed one. than it would make no difference in performance. What I wanted to imply was that most people would not use transposed ones and they would access the array row-major order. – Magavern

Answer 5

Ok, so given that the word "confusion" is literally in the title I can understand the level of...confusion.

Firstly, this absolutely is a real problem

Never, EVER succumb to the idea that "it is used be but...PC's nowadays..."

Of the primary issues here are: -Cache eviction strategy (LRU, FIFO, etc.) as @Y.C.Jung was beginning to touch on -Branch prediction -Pipelining (it's depth, etc) -Actual physical memory layout -Size of memory -Architecture of machine, (ARM, MIPS, Intel, AMD, Motorola, etc.)

This answer will focus on the Harvard architecture, Von Neumann machine as it is most applicable to the current PC.

The memory hierarchy:

https://en.wikipedia.org/wiki/File:ComputerMemoryHierarchy.svgis

Is a juxtaposition of cost versus speed.

For today's standard PC system this would be something like: SIZE: 500GB HDD > 8GB RAM > L2 Cache > L1 Cache > Registers. SPEED: 500GB HDD < 8GB RAM < L2 Cache < L1 Cache < Registers.

This leads to the idea of Temporal and Spatial locality. One means how your data is organized, (code, working set, etc.), the other means physically where your data is organized in "memory."

Given that "most" of today's PC's are little-endian (Intel) machines as of late, they lay data into memory in a specific little-endian ordering. It does differ from big-endian, fundamentally.

https://www.cs.umd.edu/class/sum2003/cmsc311/Notes/Data/endian.html (covers it rather... swiftly ;) )

(For the simplicity of this example, I am going to 'say' that things happen in single entries, this is incorrect, entire cache blocks are typically accessed and vary drastically my manufacturer, much less model).

So, now that we have that our of the way, if, hypothetically your program demanded 1GB of data from your 500GB HDD, loaded into your 8GB of RAM, then into the cache hierarchy, then eventually registers, where your program went and read the first entry from your freshest cache line just to have your second (in YOUR code) desired entry happen to be sitting in the next cache line, (i.e. the next ROW instead of column you would have a cache MISS.

Assuming the cache is full, because it is small, upon a miss, according to the eviction scheme, a line would be evicted to make room for the line that 'does' have the next data you need. If this pattern repeated you would have a MISS on EVERY attempted data retrieval!

Worse, you would be evicting lines that actually have valid data you are about to need, so you will have to retrieve them AGAIN and AGAIN.

The term for this is called: thrashing

https://en.wikipedia.org/wiki/Thrashing_(computer_science) and can indeed crash a poorly written/error prone system. (Think windows BSOD)....

On the other hand, if you had laid out the data properly, (i.e. Row major)...you WOULD still have misses!

But these misses would only occur at the end of each retrieval, not on EVERY attempted retrieval. This results in orders of magnitude of difference in system and program performance.

Very very simple snippet:

#include<stdio.h>

#define NUM_ROWS 1024
#define NUM_COLS 1024

int COL_MAJOR [NUM_ROWS][NUM_COLS];

int main (void){
        int i=0, j=0;
        for(i; i<NUM_ROWS; i++){
                for(j; j<NUM_COLS; j++){
                        COL_MAJOR[j][i]=(i+j);//NOTE i,j order here!
                }//end inner for
        }//end outer for
return 0;
}//end main

Now, compile with: gcc -g col_maj.c -o col.o

Now, run with: time ./col.o real 0m0.009s user 0m0.003s sys 0m0.004s

Now repeat for ROW major:

#include<stdio.h>

#define NUM_ROWS 1024
#define NUM_COLS 1024

int ROW_MAJOR [NUM_ROWS][NUM_COLS];

int main (void){
        int i=0, j=0;
        for(i; i<NUM_ROWS; i++){
                for(j; j<NUM_COLS; j++){
                        ROW_MAJOR[i][j]=(i+j);//NOTE i,j order here!
                }//end inner for
        }//end outer for
return 0;
}//end main

Compile: terminal4$ gcc -g row_maj.c -o row.o Run: time ./row.o real 0m0.005s user 0m0.001s sys 0m0.003s

Now, as you can see, the Row Major one was significantly faster.

Not convinced? If you would like to see a more drastic example: Make the matrix 1000000 x 1000000, initialize it, transpose it and print it to stdout. ```

(Note, on a *NIX system you WILL need to set ulimit unlimited)

ISSUES with my answer: -Optimizing compilers, they change a LOT of things! -Type of system -Please point any others out -This system has an Intel i5 processor

Shortchange

Thank you for the effort and the great explanation. I just want to make a remark. You cannot automatically assume the row-major order is "the fastest" or "the best". It depends on your application and the operation you will perform frequently. – Fremont

Did you actually read the answer? Repeatedly performing an operation that thrashes memory or unnecessarily evicts and reloads the cache due to misses will never be efficient, ever. – Shortchange

The problem is this sentence: "Now, as you can see, the Row Major one was significantly faster." For this code, for these operations you perform, this is correct. But, you cannot generalise this. – Fremont

You have to change the order of for-loops. You can't use the same order of index iteration for different memory layouts. If you change the for loops for i and j in both examples, you'll get the opposite result of what you're showing. – Sennight

Should not int COL_MAJOR [NUM_ROWS][NUM_COLS]; be instead int COL_MAJOR [NUM_COLS][NUM_ROWS];? – Micaelamicah

Answer 6

It's easy:row-major and column-major are from the glUniformMatrix*()'s perspective. actually, matrix never changed, it is alwarys:

What is difference is matrix class realization. It deterimins how 16 floats stored as parameter passing to glUniformMatrix*()

If you use row-major matrix, memory of 4x4 matrix is: (a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34, a41, a42, a43, a44), else for column-major is: (a11, a21, a31, a41, a12, a22, a32, a42, a13, a23, a33, a43, a41, a42, a43, a44).

Because glsl is column-major matrix, so it will read the 16 float data (b1, b2, b3, b4, b5, b6, b7, b8, b9, b10, b11, b12, b13, b14, b15, b16) as

Since in row-major, a11=b1, a12=b2, a13=b3, a14=b4, a21=b5, a22=b6,...so in glsl matrix is changed to

while in column-major: a11=b1, a21=b2, a31=b3, a41=b4, a12=b5, a22=b6,...so in glsl matrix is changed to

which is the same as the orign. So row-major needing a transpose while column-major not.

Runnel

Answer 7

A short addendum to above answers. In terms of C, where memory is accessed almost directly, the row-major or column-major order affects your program in 2 ways: 1. It affects the layout of your matrix in memory 2. The order of element access that must be kept - in the form of ordering loops.

1. is explained quite thoroughly in the previous answers, so I will add to 2.

eulerworks answer points out that in his example, using row major matrix brought about significant slow down in calculation. Well, he is right, but the result can be at the same time reversed.

The loop order was for(over rows) { for(over columns) { do something over a matrix } }. Which means that the dual loop will access elements in a row and then move over to the next row. For example, A(0,1) -> A(0,2) -> A(0,3) -> ... -> A(0,N_ROWS) -> A(1,0) -> ...

In such case, if A was stored in row major format there would be minimal cache misses since the elements will probably lined up in linear fashion in memory. Otherwise in column-major format, memory access will jump around using N_ROWS as a stride. So row-major is faster in the case.

Now, we can actually switch the loop, such that it will for(over columns) { for(over rows) { do something over a matrix } }. For this case, the result will be exactly the opposite. Column major calculation will be faster since the loop will read elements in columns in linear fashion.

Hence, you might as well remember this: 1. Selecting row major or column major storage format is up to your taste, even though the traditional C programming community seem to prefer the row-major format. 2. Although you are pretty much free to choose whatever you may like, you need to be consistent with the notion of the indexing. 3. Also, this is quite important, keep in mind that when writing down your own algorithms, try to order the loops so that it will honor the storage format of your choice. 4. Be consistent.

Ideography

Can you format the code and content to make this more readable? For instance use the ordered list and syntax highlighting properly. – Plover

Answer 8

Given the explanations above, here is a code snippet demonstrating the concept.

//----------------------------------------------------------------------------------------
// A generalized example of row-major, index/coordinate conversion for
// one-/two-dimensional arrays.
// ex: data[i] <-> data[r][c]
//
// Sandboxed at: http://swift.sandbox.bluemix.net/#/repl/5a077c462e4189674bea0810
//
// -eholley
//----------------------------------------------------------------------------------------

// Algorithm

let numberOfRows    = 3
let numberOfColumns = 5
let numberOfIndexes = numberOfRows * numberOfColumns

func index(row: Int, column: Int) -> Int {
    return (row * numberOfColumns) + column
}

func rowColumn(index: Int) -> (row: Int, column: Int) {
    return (index / numberOfColumns, index % numberOfColumns)
}

//----------------------------------------------------------------------------------------

// Testing

let oneDim = [
       0,    1,    2,    3,    4,
       5,    6,    7,    8,    9,
      10,   11,   12,   13,   14,
]

let twoDim = [
    [  0,    1,    2,    3,    4 ],
    [  5,    6,    7,    8,    9 ],
    [ 10,   11,   12,   13,   14 ],
]

for i1 in 0..<numberOfIndexes {
    let v1 = oneDim[i1]
    let rc = rowColumn(index: i1)
    let i2 = index(row: rc.row, column: rc.column)
    let v2 = oneDim[i2]
    let v3 = twoDim[rc.row][rc.column]
    print(i1, v1, i2, v2, v3, rc)
    assert(i1 == i2)
    assert(v1 == v2)
    assert(v2 == v3)
}

/* Output:
0 0 0 0 0 (row: 0, column: 0)
1 1 1 1 1 (row: 0, column: 1)
2 2 2 2 2 (row: 0, column: 2)
3 3 3 3 3 (row: 0, column: 3)
4 4 4 4 4 (row: 0, column: 4)
5 5 5 5 5 (row: 1, column: 0)
6 6 6 6 6 (row: 1, column: 1)
7 7 7 7 7 (row: 1, column: 2)
8 8 8 8 8 (row: 1, column: 3)
9 9 9 9 9 (row: 1, column: 4)
10 10 10 10 10 (row: 2, column: 0)
11 11 11 11 11 (row: 2, column: 1)
12 12 12 12 12 (row: 2, column: 2)
13 13 13 13 13 (row: 2, column: 3)
14 14 14 14 14 (row: 2, column: 4)
*/

Flair

Answer 9

This is what I wanted to know:

1. glm matrices are laid out in memory as contiguous rows. No different than row major matrices.
2. The difference is the implementation of operator*.
   Row major operator* is row * column.
   Column major (glm) operator* is column * row.

Example mat = [a,b;c,d] looks like a,b,c,d in memory for both row and column major (in the glm imlementation of column major).
Row major: [a,b;c,d] * [x;y] = [ax+by;cx+dy]
Column major: [a,b;c,d] * [x,y] = [ax+cy,bx+dy]

I ran this test code to find out:

void Learn_glm2() {
    const glm::mat3 mat_123{ { 1,2,3 }, { 4,5,6 }, { 7,8,9 } }; // It is laid out row major in memory.
    const glm::mat3 mat_234{ { 2,3,4 }, { 5,6,7 }, { 8,9,10 } };
    glm::vec3 vec_123 = glm::vec3{ 1,2,3 };
    auto res = mat_123 * vec_123; // The result is not the same as a row major multiply.
    auto res2 = vec_123 * mat_123; // This is the same as mat_123 * vec_123 in row major.
    auto res3 = mat_123 * mat_234; // This is the same as mat_234 * mat_123 in row major.
    auto tranlate_mat = glm::translate( vec_123 ); // This is the transpose of a row major translation matrix, but still contiguous rows im memory.
    int a = 0; // Set break point here and inspect the result.
}

In Visual studio, you can see the memory layout in the memory inspector window.

This does matter if you construct your own matrices. OP wanted to know how this works.

If you write your own code and went to university, then column major is likely an annoyance so, instead of glm, I use my own row major math library on the CPU side and use reverse multiplication order in the shaders: gl_position = vertex_pos * MVP. Or transpose the row major matrices before uploading to the shaders.

Pelham

Answer 10

Today there is no reason to use other then column-major order, there are several libraries that support it in c/c++ (eigen,armadillo,...). Furthermore column-major order is more natural, eg. pictures with [x,y,z] are stored slice by slice in file, this is column-major order. While in two dimension it may be confusing to choose better order, in higher dimension it is quite clear that column-major order is the only solution in many situation.

Authors of C created concept of arrays but perhaps they did not expect that somebody had used it as a matrices. I would be shocked myself if I saw how arrays are used in place where already everything was made up in fortran and column-major order. I think that row-major order is simply alternative to column-major order but only in situation where it is really needed (for now I don't know about any).

It is strangely that still someone creates library with row-major order. It is unnecessary waste of energy and time. I hope that one day everything will be column-major order and all confusions simply disappear.

Ger