ReLU derivative in backpropagation

Question

I am about making backpropagation on a neural network that uses ReLU. In a previous project of mine, I did it on a network that was using Sigmoid activation function, but now I'm a little bit confused, since ReLU doesn't have a derivative.

Here's an image about how weight5 contributes to the total error. In this example, out/net = a*(1 - a) if I use sigmoid function.

What should I write instead of "a*(1 - a)" to make the backpropagation work?

Keavy

Depends on the actual ReLU expression. There are several ReLUs that can be used. Nevertheless, it's just the derivative of the ReLU function with respect to its argument. And you can compute that either by hand or using e.g. wolfram alpha. Or just google it. – Sequestrate

Answer 1

since ReLU doesn't have a derivative.

No, ReLU has derivative. I assumed you are using ReLU function f(x)=max(0,x). It means if x<=0 then f(x)=0, else f(x)=x. In the first case, when x<0 so the derivative of f(x) with respect to x gives result f'(x)=0. In the second case, it's clear to compute f'(x)=1.

Barring

I had a feeling that's going to be the solution, but I wasn't sure, especially about f'(x)=0. Thanks for the answer :) – Keavy

I just want to say that the OP is correct, from a pure mathematical standpoint, in saying that "ReLU doesn't have a derivative". This is true because of one point in its domain that makes the derivative undefined. This is easy to see if we just visualize the function. But we simply adopt a convention (i.e. that the derivative is 0 at x=0) and pretend that the function is differentiable, but this is not strictly true. – Diffluent

Hi, I have a question. Will the derivative of ReLU during x<0 (which is f'(x)=0) causes the dead neuron problem? I am confused which actually contribute to the problem of the dead neuron. During forward past of backward past, or both? – Encasement

@Diffluent your comment should be the accepted answer. – Homozygous

Answer 2

Relu Derivative is 1 for x >= 0 and 0 for x < 0

Saad

1 for x>0, not x>=0. – Kalie

Answer 3

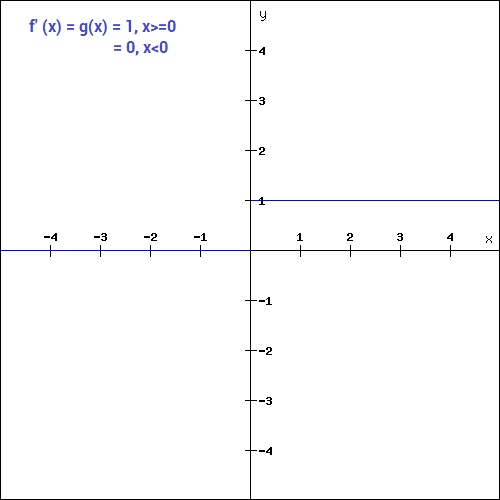
While ReLU is common, the derivative can be confusing, part of the reason is that it is in theory not defined at x=0, in practice, we just use f'(x=0)=0.

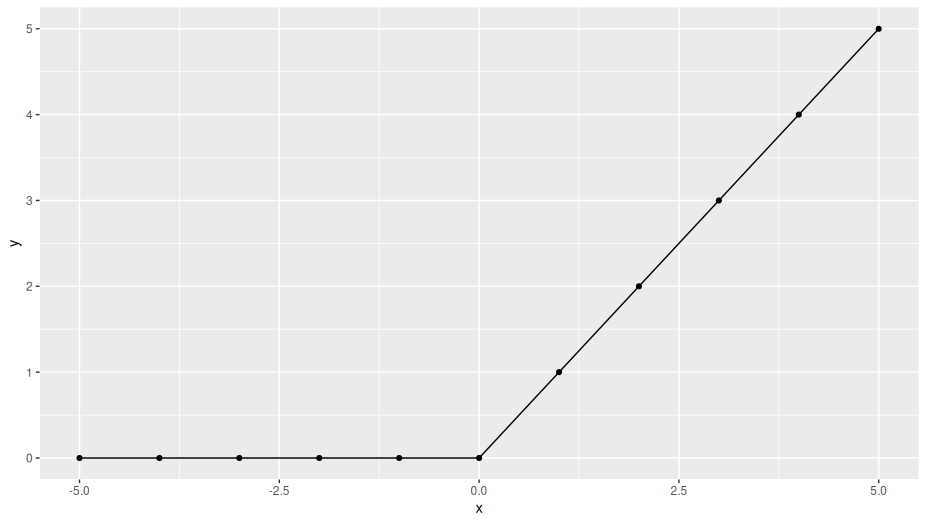
This is assuming by ReLU (Rectified Linear Unit) is meant y=max(0,x). This function looks like so:

For the part where x>0 it is fairly easy to see what the derivative is. For every 1 that x increases, y increases by 1 (as we can also see from the function definition ofcourse), the derivative here is thus f'(x>0)=1.

For the part where x<0 it is fairly easy to see that the line is level, i.e. the slope is flat or 0. Here we thus have f'(x<0)=0.

The tricky (but not terribly important in practice) part comes at x=0. The Left-Hand Side (LHS) and Right-Hand Side (RHS) of the derivative here are not equal, in theory it is thus undefined.

In practice we normally just use: f'(x=0)=0. But you can also use f'(x=0)=1, try it out.

Why can we just do that? Remember that we use these derivates to scale the weight updates. Normally the weight updates are scaled in all kinds of other ways (learning rate, etc.). Scaling by 0 of course does mean that no update is made, this also happens e.g. with Hinton's dropout. Remember also that what you're computing of is the derivative of the error term (at the output layer), if the error term is 0...

Otiose

The only complete and correct answer here. Another way to build intuition for why the derivative is technically not defined at x=0 is to talk about the tangent at x=0. What slope should it have? Right ... – Homozygous

I understand better, thanks. Let me add. All x and y here represent graph coordinates. y = x always has gradient = m = 1 y = mx + c: c = 0, m = 1. In the image, put a vertical line on point (x:0, y:0), representing y-axis. On the left of the line, you can see that gradient is always 0 and on right, gradient is always 1. m of ReLU is always 0 for -ve values or 1 for +ve values. Derivative of a function is the slope of the graph of the function, or, the slope of the tangent line at a point. Every increase in x is same increase in y because, m = 1. – Dissimilation

m = 0 when line is completely horizontal. – Dissimilation

Answer 4

The relu derivative can be implemented with np.heaviside step function e.g. np.heaviside(x, 1). The second parameter defines the return value when x = 0, so a 1 means 1 when x = 0.

Mack

Answer 5

Coming to this from a maths standpoint it should be half on the discontinuity. Its quote common to average things like that since frouiers series act in that manner

Reece

Answer 6

It's technically the same as x * max(0, x) / x

Restaurateur

Answer 7

The best drop-in replacement for what you are looking for is:

if f(x) = max(0, x) then f'(x) = gradient = out/net = f(x) / x.

This works because for values zero and below, we get 0/x = 0. For values greater than zero, f(x)=x so we get x/x = 1.

Bosworth