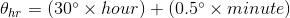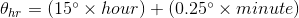Find angle between hour and minute hands in an analog clock

Question

I was given this interview question recently:

Given a 12-hour analog clock, compute in degree the smaller angle between the hour and minute hands. Be as precise as you can.

I'm wondering what's the simplest, most readable, most precise algorithm is. Solution in any language is welcome (but do explain it a bit if you think it's necessary).

Repetend

simplest? looking it up on wiki! : en.wikipedia.org/wiki/Clock_angle_problem' – Toner

I think that this is a purely mathematical problem, and also fairly trivial. I do not see how this question can get four up-votes... – Rebekahrebekkah

Answer 1

It turns out that Wikipedia does have the best answer:

// h = 1..12, m = 0..59
static double angle(int h, int m) {
    double hAngle = 0.5D * (h * 60 + m);
    double mAngle = 6 * m;
    double angle = Math.abs(hAngle - mAngle);
    angle = Math.min(angle, 360 - angle);
    return angle;
}

Basically:

• The hour hand moves at the rate of 0.5 degrees per minute
• The minute hand moves at the rate of of 6 degrees per minute

Problem solved.

---

And precision isn't a concern because the fractional part is either .0 or .5, and in the range of 0..360, all of these values are exactly representable in double.

Repetend

@starblue: I've clarified that it's a 12-hour analog clock. – Repetend

@starblue Can analog clock be ever 24hr? – Crenulate

Why it is 30/60=0.5D? Why not 330/60=5.5D? – Hideout

@starblue just do a hour%12 and you would be fine. – Jorgenson

How is 12:15 not a 90 degree angle? Wouldn't the pointing to the 12 make a 90 degree angle with the 3 if the clock is a perfect circle? – Bonbon

that's because by the time 15 minutes went by, the hour-pointer would have traveled one quarter of the way to 1 o'clock. – Galluses

Answer 2

For finding the angle between the hands of a clock is ,

30 * [HRS - (MIN/5)] + (MIN/2) 

Rammish

Missing absolute value ? – Herta

Please explain 5 and 2 values. describe calculation of these two values. where these come from. – Midas

Answer 3

The java code that polygenlubricants is similar than mine. Let's assume that the clock is 12 hour instead of 24.

If it's 24 hours, then that's a different story. Also, another assumption, assume if the clock is stopped while we calculate this.

One clock cycle is 360 degree.

1. How many degree can the minute hand run per minute? 360 / 60 = 6 degree per minute.

2. How many degree can the hour hand run per hour? 360/12 = 30 degree per hour (since hour hand run slower than minute)

Since it's easier to calculate in the unit, "minute", let's get

"how many degree can the hour hand run per minute"?

30 / 60 = 0.5 degree per minute.

So, if you know how to get those numbers, the problem is pretty much solved with this partial mathematical solution.

Hep

Answer 4

Try this code :

import java.util.Scanner;

class Clock{

    public static void main(String args[]){
        int hours,mins;

    System.out.println("Enter the Time(hours) : ");
        Scanner dx = new Scanner(System.in);
        hours = dx.nextInt();

    System.out.println("Enter the time(mins) : ");
        Scanner fx = new Scanner(System.in);
        mins = fx.nextInt();

    if(hours>=0 && hours<=12){

        if(mins>=0 && mins<=59){
            double hDegrees = (hours * 30) + (mins * 0.5);
                    double mDegrees = mins * 6;
                    double diff  = Math.abs(hDegrees - mDegrees);

        System.out.println("The angle between sticks is (degrees) : "+diff);
                if (diff > 180){ 

                diff = 360 - diff;
        System.out.println("The angle between sticks is (degrees) : "+diff);
                }

        }

    }

    else{
        System.out.println("Wrong input ");
    }


}

}

Yves

Answer 5

Minute angle (from 12 o’clock): 360 * minutes / 60

Hour angle (from 12 o’clock): 360 * (hour % 12) / 12 + 360 * (minutes / 60) * (1 / 12)

Angle between hour and minute: (hour angle - minute angle) % 360 By simple arithmetic, this reduces to 30 * hours - 5.5 * minutes.

Sherer

Answer 6

    **php code for find angle via time (minutes and hour's)**

    echo calcAngle(3,70);

function calcAngle($h, $m)
{
    // validate the input
    if ($h <0 || $m < 0 || $h >12 || $m > 60)
      {
       return "Wrong input";
      }
      else {

    if ($h == 12) $h = 0;
    if ($m == 60) $m = 0;

    $hour_angle = 0.5 * ($h*60 + $m);
    $minute_angle = 6*$m;
    $angle = abs($hour_angle - $minute_angle);
    $angle = min(360-$angle, $angle);

    return $angle;
}
}

Ridgepole

Answer 7

The problem is known as a “Clock Angle Problem” where we need to find the angle between the hands (hour & minute) of an analog clock at a particular time.

Solution in C Programming Language.

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<inttypes.h>
#include<assert.h>

#define STRING_LENGTH 6

double angle_between_hour_min_hand(char[]);

int main(void) {
    uint8_t test;
    printf("Enter the number of test cases\n");
    scanf("%"SCNu8,&test);
    assert(test>0);
    while(test--) {
        char time_digital[STRING_LENGTH];
        printf("Enter the time\n");
        scanf("%s",time_digital);
        double angle_between_hands_deg = angle_between_hour_min_hand(time_digital);
        abs(angle_between_hands_deg) < angle_between_hands_deg ? printf("%0.1f\n",angle_between_hands_deg) : printf("%d\n",abs(angle_between_hands_deg));
    }
    return 0;
}

double angle_between_hour_min_hand(char time_digital[]) {
    uint8_t hr,min;
    double hr_angle_deg,min_angle_deg,angle_between_hands_deg;
    char*buffer = calloc(sizeof(char),STRING_LENGTH);
    if(buffer) {
        snprintf(buffer,STRING_LENGTH,"%s",time_digital);
        hr = atoi(__strtok_r(buffer,":",&buffer));
        min = atoi(__strtok_r(NULL,":",&buffer));
        buffer -= strlen(time_digital);
        free(buffer);
        hr_angle_deg = (double)(30*hr) + (double) (0.5*min);
        // printf("hr-angle: %f\n", hr_angle_deg);
        min_angle_deg = 6*min;
        // printf("min-angle: %f\n", min_angle_deg);
        angle_between_hands_deg = (hr_angle_deg > min_angle_deg) ? hr_angle_deg - min_angle_deg : min_angle_deg - hr_angle_deg;
        if(angle_between_hands_deg > 180) {
            angle_between_hands_deg = 360 - angle_between_hands_deg;
        }
    }
    else fprintf(stderr,"Memory not allocated to the buffer pointer!\n");
    return angle_between_hands_deg;
}

Compile the above program in your system, I used Ubuntu 18.04 LTS Bionic Beaver, you can use any system which has a C compiler installed.

gcc -Wall -g clock_angle_sol.c -o clock_angle_sol
./clock_angle_sol
Enter the time in 12-hour or 24 hour i.e (hr:min) format: 12:45
Angle: 112.00 degrees.

Notes:
1. The equation will give you the angle made by hour hand in 12-hour clock.
2. If you want to calculate the angle made by hour hand in a 24-hour clock, then use the following equation:
3. Second hand also contribute to the rotation of the minute hand, but we ignored it because the contribution is insignificant i.e. 1/10 = 0.1.

Shoffner

Answer 8

This is one solution (C#). This is a very simple solution and ignores precision. Hope the solution is self explanatory.

public static double GetAngle(int hourHand, int minuteHand)
    {
        double oneMinuteAngle = (360 / 60);
        double oneHourAngle = (360 / 12);

        double hourAngle = oneHourAngle * hourHand;
        double minuteAngle = oneMinuteAngle * minuteHand;

        return (Math.Abs(hourAngle - minuteAngle));
    }

Handicapper

This answer is wrong. At 1:30, the hour hand is half way between 1 and 2... – Battlefield

Answer 9

I do not know if it's right, .something like this?

//m*360/60 - (h*360/24)+(m*360/(24*60)) ->
t = abs(25*m - 60*h)/4
t = min(t,360-t)

Concurrent

Well it can't be right if you're missing an end parenthesis :D – Robbie

For h=3, m=0, I get 45. It should be 90. – Repetend

@poly okay, I forgot regular clock is 12, not 24 hours. if you replace division by 24 with 12, you should get correct – Concurrent

Answer 10

for finding the angle between the hour hand and the minute hand is

angle=(hour*5-min)*6

Michealmicheil

What are the issues with this answer? – Monochromat