I am solving a problem on directed acyclic graph.
But I am having trouble testing my code on some directed acyclic graphs. The test graphs should be large, and (obviously) acyclic.
I tried a lot to write code for generating acyclic directed graphs. But I failed every time.
Is there some existing method to generate acyclic directed graphs I could use?
I cooked up a C program that does this. The key is to 'rank' the nodes, and only draw edges from lower ranked nodes to higher ranked ones.
The program I wrote prints in the DOT language.
Here is the code itself, with comments explaining what it means:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MIN_PER_RANK 1 /* Nodes/Rank: How 'fat' the DAG should be. */
#define MAX_PER_RANK 5
#define MIN_RANKS 3 /* Ranks: How 'tall' the DAG should be. */
#define MAX_RANKS 5
#define PERCENT 30 /* Chance of having an Edge. */
int main (void)
{
int i, j, k,nodes = 0;
srand (time (NULL));
int ranks = MIN_RANKS
+ (rand () % (MAX_RANKS - MIN_RANKS + 1));
printf ("digraph {\n");
for (i = 0; i < ranks; i++)
{
/* New nodes of 'higher' rank than all nodes generated till now. */
int new_nodes = MIN_PER_RANK
+ (rand () % (MAX_PER_RANK - MIN_PER_RANK + 1));
/* Edges from old nodes ('nodes') to new ones ('new_nodes'). */
for (j = 0; j < nodes; j++)
for (k = 0; k < new_nodes; k++)
if ( (rand () % 100) < PERCENT)
printf (" %d -> %d;\n", j, k + nodes); /* An Edge. */
nodes += new_nodes; /* Accumulate into old node set. */
}
printf ("}\n");
return 0;
}
And here is the graph generated from a test run:
dot program supplied with the GraphWiz package. –
Costa The answer to https://mathematica.stackexchange.com/questions/608/how-to-generate-random-directed-acyclic-graphs applies: if you have a adjacency matrix representation of the edges of your graph, then if the matrix is lower triangular, it's a DAG by necessity.
A similar approach would be to take an arbitrary ordering of your nodes, and then consider edges from node x to y only when x < y. That constraint should also get your DAGness by construction. Memory comparison would be one arbitrary way to order your nodes if you're using structs to represent nodes.
Basically, the pseudocode would be something like:
for(i = 0; i < N; i++) {
for (j = i+1; j < N; j++) {
maybePutAnEdgeBetween(i, j);
}
}
where N is the number of nodes in your graph.
The pseudocode suggests that the number of potential DAGs, given N nodes, is
2^(n*(n-1)/2),
since there are
n*(n-1)/2
ordered pairs ("N choose 2"), and we can choose either to have the edge between them or not.
maybePutAnEdgeBetween procedure would need to facilitate that. –
Unmixed So, to try to put all these reasonable answers together:
(In the following, I used V for the number of vertices in the generated graph, and E for the number of edges, and we assume that E ≤ V(V-1)/2.)
Personally, I think the most useful answer is in a comment, by Flavius, who points at the code at http://condor.depaul.edu/rjohnson/source/graph_ge.c. That code is really simple, and it's conveniently described by a comment, which I reproduce:
To generate a directed acyclic graph, we first
generate a random permutation dag[0],...,dag[v-1].
(v = number of vertices.)
This random permutation serves as a topological
sort of the graph. We then generate random edges of the
form (dag[i],dag[j]) with i < j.
In fact, what the code does is generate the request number of edges by repeatedly doing the following:
The problem with this solution is that as E gets closes to the maximum number of edges V(V-1)/2, then the algorithm becomes slower and slower, because it has to reject more and more edges. A better solution would be to make a vector of all V(V-1)/2 possible edges; randomly shuffle it; and select the first (requested edges) edges in the shuffled list.
The reservoir sampling algorithm lets us do this in space O(E), since we can deduce the endpoints of the kth edge from the value of k. Consequently, we don't actually have to create the source vector. However, it still requires O(V2) time.
Alternatively, one can do a Fisher-Yates shuffle (or Knuth shuffle, if you prefer), stopping after E iterations. In the version of the FY shuffle presented in Wikipedia, this will produce the trailing entries, but the algorithm works just as well backwards:
// At the end of this snippet, a consists of a random sample of the
// integers in the half-open range [0, V(V-1)/2). (They still need to be
// converted to pairs of endpoints).
vector<int> a;
int N = V * (V - 1) / 2;
for (int i = 0; i < N; ++i) a.push_back(i);
for (int i = 0; i < E; ++i) {
int j = i + rand(N - i);
swap(a[i], a[j]);
a.resize(E);
This requires only O(E) time but it requires O(N2) space. In fact, this can be improved to O(E) space with some trickery, but an SO code snippet is too small to contain the result, so I'll provide a simpler one in O(E) space and O(E log E) time. I assume that there is a class DAG with at least:
class DAG {
// Construct an empty DAG with v vertices
explicit DAG(int v);
// Add the directed edge i->j, where 0 <= i, j < v
void add(int i, int j);
};
Now here goes:
// Return a randomly-constructed DAG with V vertices and and E edges.
// It's required that 0 < E < V(V-1)/2.
template<typename PRNG>
DAG RandomDAG(int V, int E, PRNG& prng) {
using dist = std::uniform_int_distribution<int>;
// Make a random sample of size E
std::vector<int> sample;
sample.reserve(E);
int N = V * (V - 1) / 2;
dist d(0, N - E); // uniform_int_distribution is closed range
// Random vector of integers in [0, N-E]
for (int i = 0; i < E; ++i) sample.push_back(dist(prng));
// Sort them, and make them unique
std::sort(sample.begin(), sample.end());
for (int i = 1; i < E; ++i) sample[i] += i;
// Now it's a unique sorted list of integers in [0, N-E+E-1]
// Randomly shuffle the endpoints, so the topological sort
// is different, too.
std::vector<int> endpoints;
endpoints.reserve(V);
for (i = 0; i < V; ++i) endpoints.push_back(i);
std::shuffle(endpoints.begin(), endpoints.end(), prng);
// Finally, create the dag
DAG rv;
for (auto& v : sample) {
int tail = int(0.5 + sqrt((v + 1) * 2));
int head = v - tail * (tail - 1) / 2;
rv.add(head, tail);
}
return rv;
}
You could generate a random directed graph, and then do a depth-first search for cycles. When you find a cycle, break it by deleting an edge.
I think this is worst case O(VE). Each DFS takes O(V), and each one removes at least one edge (so max E)
If you generate the directed graph by uniformly random selecting all V^2 possible edges, and you DFS in random order and delete a random edge - this would give you a uniform distribution (or at least close to it) over all possible dags.
A very simple approach is:
Randomly assign edges by iterating over the indices of a lower diagonal matrix (as suggested by a link above: https://mathematica.stackexchange.com/questions/608/how-to-generate-random-directed-acyclic-graphs)
This will give you a DAG with possibly more than one component. You can use a Disjoint-set data structure to give you the components that can then be merged by creating edges between the components.
Disjoint-sets are described here: https://en.wikipedia.org/wiki/Disjoint-set_data_structure
Edit: I initially found this post while I was working with a scheduling problem named flexible job shop scheduling problem with sequencing flexibility where jobs (the order in which operations are processed) are defined by directed acyclic graphs. The idea was to use an algorithm to generate multiple random directed graphs (jobs) and create instances of the scheduling problem to test my algorithms. The code at the end of this post is a basic version of the one I used to generate the instances. The instance generator can be found here.
I translated to Python and integrated some functionalities to create a transitive set of the random DAG. In this way, the graph generated has the minimum number of edges with the same reachability.
The transitive graph can be visualized at http://dagitty.net/dags.html by pasting the output in Model code (in the right).
Python version of the algorithm
import random
class Graph:
nodes = []
edges = []
removed_edges = []
def remove_edge(self, x, y):
e = (x,y)
try:
self.edges.remove(e)
# print("Removed edge %s" % str(e))
self.removed_edges.append(e)
except:
return
def Nodes(self):
return self.nodes
# Sample data
def __init__(self):
self.nodes = []
self.edges = []
def get_random_dag():
MIN_PER_RANK = 1 # Nodes/Rank: How 'fat' the DAG should be
MAX_PER_RANK = 2
MIN_RANKS = 6 # Ranks: How 'tall' the DAG should be
MAX_RANKS = 10
PERCENT = 0.3 # Chance of having an Edge
nodes = 0
ranks = random.randint(MIN_RANKS, MAX_RANKS)
adjacency = []
for i in range(ranks):
# New nodes of 'higher' rank than all nodes generated till now
new_nodes = random.randint(MIN_PER_RANK, MAX_PER_RANK)
# Edges from old nodes ('nodes') to new ones ('new_nodes')
for j in range(nodes):
for k in range(new_nodes):
if random.random() < PERCENT:
adjacency.append((j, k+nodes))
nodes += new_nodes
# Compute transitive graph
G = Graph()
# Append nodes
for i in range(nodes):
G.nodes.append(i)
# Append adjacencies
for i in range(len(adjacency)):
G.edges.append(adjacency[i])
N = G.Nodes()
for x in N:
for y in N:
for z in N:
if (x, y) != (y, z) and (x, y) != (x, z):
if (x, y) in G.edges and (y, z) in G.edges:
G.remove_edge(x, z)
# Print graph
for i in range(nodes):
print(i)
print()
for value in G.edges:
print(str(value[0]) + ' ' + str(value[1]))
get_random_dag()
Bellow, you may see in the figure the random DAG with many redundant edges generated by the Python code above.
I adapted the code to generate the same graph (same reachability) but with the least possible number of edges. This is also called transitive reduction.
def get_random_dag():
MIN_PER_RANK = 1 # Nodes/Rank: How 'fat' the DAG should be
MAX_PER_RANK = 3
MIN_RANKS = 15 # Ranks: How 'tall' the DAG should be
MAX_RANKS = 20
PERCENT = 0.3 # Chance of having an Edge
nodes = 0
node_counter = 0
ranks = random.randint(MIN_RANKS, MAX_RANKS)
adjacency = []
rank_list = []
for i in range(ranks):
# New nodes of 'higher' rank than all nodes generated till now
new_nodes = random.randint(MIN_PER_RANK, MAX_PER_RANK)
list = []
for j in range(new_nodes):
list.append(node_counter)
node_counter += 1
rank_list.append(list)
print(rank_list)
# Edges from old nodes ('nodes') to new ones ('new_nodes')
if i > 0:
for j in rank_list[i - 1]:
for k in range(new_nodes):
if random.random() < PERCENT:
adjacency.append((j, k+nodes))
nodes += new_nodes
for i in range(nodes):
print(i)
print()
for edge in adjacency:
print(str(edge[0]) + ' ' + str(edge[1]))
print()
print()
Result:
Here's an simple algorithm for generating a random DAG that might not be connected.
const randomDAG = (x, n) => {
const length = n * (n - 1) / 2;
const dag = new Array(length);
for (let i = 0; i < length; i++) {
dag[i] = Math.random() < x ? 1 : 0;
}
return dag;
};
const dagIndex = (n, i, j) => n * i + j - (i + 1) * (i + 2) / 2;
const dagToDot = (n, dag) => {
let dot = "digraph {\n";
for (let i = 0; i < n; i++) {
dot += ` ${i};\n`;
for (let j = i + 1; j < n; j++) {
const k = dagIndex(n, i, j);
if (dag[k]) dot += ` ${i} -> ${j};\n`;
}
}
return dot + "}";
};
const randomDot = (x, n) => dagToDot(n, randomDAG(x, n));
new Viz().renderSVGElement(randomDot(0.3, 10)).then(svg => {
document.body.appendChild(svg);
});<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/viz.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/full.render.js"></script>If you run this code snippet a couple of times, you might see a DAG which is not connected.
A directed acyclic graph (DAG) is just a topologically sorted undirected graph. An undirected graph of n vertices can have a maximum of n * (n - 1) / 2 edges, not counting repeated edges or edges from a vertex to itself. Now, you can only have an edge from a lower vertex to a higher vertex. Hence, the direction of all the edges are predetermined.
This means that you can represent the entire DAG using a one dimensional array of n * (n - 1) / 2 edge weights. An edge weight of 0 means that the edge is absent. Hence, we just create a random array of zeros or ones, and that's our random DAG.
An edge from vertex i to vertex j in a DAG of n vertices, where i < j, has an edge weight at index k where k = n * i + j - (i + 1) * (i + 2) / 2.
Once you generate a random DAG, you can check if it's connected using the following function.
const isConnected = (n, dag) => {
const reached = new Array(n).fill(false);
reached[0] = true;
const queue = [0];
while (queue.length > 0) {
const x = queue.shift();
for (let i = 0; i < n; i++) {
if (i === n || reached[i]) continue;
const j = i < x ? dagIndex(n, i, x) : dagIndex(n, x, i);
if (dag[j] === 0) continue;
reached[i] = true;
queue.push(i);
}
}
return reached.every(x => x); // return true if every vertex was reached
};
If it's not connected then its complement will always be connected.
const complement = dag => dag.map(x => x ? 0 : 1);
const randomConnectedDAG = (x, n) => {
const dag = randomDAG(x, n);
return isConnected(n, dag) ? dag : complement(dag);
};
Note that if we create a random DAG with 30% edges then its complement will have 70% edges. Hence, the only safe value for x is 50%. However, if you care about connectivity more than the percentage of edges then this shouldn't be a deal breaker.
Finally, putting it all together.
const randomDAG = (x, n) => {
const length = n * (n - 1) / 2;
const dag = new Array(length);
for (let i = 0; i < length; i++) {
dag[i] = Math.random() < x ? 1 : 0;
}
return dag;
};
const dagIndex = (n, i, j) => n * i + j - (i + 1) * (i + 2) / 2;
const isConnected = (n, dag) => {
const reached = new Array(n).fill(false);
reached[0] = true;
const queue = [0];
while (queue.length > 0) {
const x = queue.shift();
for (let i = 0; i < n; i++) {
if (i === n || reached[i]) continue;
const j = i < x ? dagIndex(n, i, x) : dagIndex(n, x, i);
if (dag[j] === 0) continue;
reached[i] = true;
queue.push(i);
}
}
return reached.every(x => x); // return true if every vertex was reached
};
const complement = dag => dag.map(x => x ? 0 : 1);
const randomConnectedDAG = (x, n) => {
const dag = randomDAG(x, n);
return isConnected(n, dag) ? dag : complement(dag);
};
const dagToDot = (n, dag) => {
let dot = "digraph {\n";
for (let i = 0; i < n; i++) {
dot += ` ${i};\n`;
for (let j = i + 1; j < n; j++) {
const k = dagIndex(n, i, j);
if (dag[k]) dot += ` ${i} -> ${j};\n`;
}
}
return dot + "}";
};
const randomConnectedDot = (x, n) => dagToDot(n, randomConnectedDAG(x, n));
new Viz().renderSVGElement(randomConnectedDot(0.3, 10)).then(svg => {
document.body.appendChild(svg);
});<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/viz.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/full.render.js"></script>If you run this code snippet a couple of times, you may see a DAG with a lot more edges than others.
If you care about both connectivity and having a certain percentage of edges then you can use the following algorithm.
It should be noted that this algorithm is not as efficient as the previous method.
const randomDAG = (x, n) => {
const length = n * (n - 1) / 2;
const dag = new Array(length).fill(1);
for (let i = 0; i < length; i++) {
if (Math.random() < x) continue;
dag[i] = 0;
if (!isConnected(n, dag)) dag[i] = 1;
}
return dag;
};
const dagIndex = (n, i, j) => n * i + j - (i + 1) * (i + 2) / 2;
const isConnected = (n, dag) => {
const reached = new Array(n).fill(false);
reached[0] = true;
const queue = [0];
while (queue.length > 0) {
const x = queue.shift();
for (let i = 0; i < n; i++) {
if (i === n || reached[i]) continue;
const j = i < x ? dagIndex(n, i, x) : dagIndex(n, x, i);
if (dag[j] === 0) continue;
reached[i] = true;
queue.push(i);
}
}
return reached.every(x => x); // return true if every vertex was reached
};
const dagToDot = (n, dag) => {
let dot = "digraph {\n";
for (let i = 0; i < n; i++) {
dot += ` ${i};\n`;
for (let j = i + 1; j < n; j++) {
const k = dagIndex(n, i, j);
if (dag[k]) dot += ` ${i} -> ${j};\n`;
}
}
return dot + "}";
};
const randomDot = (x, n) => dagToDot(n, randomDAG(x, n));
new Viz().renderSVGElement(randomDot(0.3, 10)).then(svg => {
document.body.appendChild(svg);
});<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/viz.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/viz.js/2.1.2/full.render.js"></script>Hope that helps.
Create a graph with n nodes and an edge between each pair of node n1 and n2 if n1 != n2 and n2 % n1 == 0.
I recently tried re-implementing the accepted answer and found that it is indeterministic. If you don't enforce the min_per_rank parameter, you could end up with a graph with 0 nodes.
To prevent this, I wrapped the for loops in a function and then checked to make sure that, after each rank, that min_per_rank was satisfied. Here's the JavaScript implementation:
https://github.com/karissa/random-dag
And some pseudo-C code that would replace the accepted answer's main loop.
int pushed = 0
int addRank (void)
{
for (j = 0; j < nodes; j++)
for (k = 0; k < new_nodes; k++)
if ( (rand () % 100) < PERCENT)
printf (" %d -> %d;\n", j, k + nodes); /* An Edge. */
if (pushed < min_per_rank) return addRank()
else pushed = 0
return 0
}
To test algorithms I generated random graphs based on node layers. This is the Python script (also print the adjacency list). You can change the nodes connection probability percentages or add layers to have a slightly different or "taller" graphs:
# Weighted DAG generator by forward layers
import argparse
import random
parser = argparse.ArgumentParser("dag_gen2")
parser.add_argument(
"--layers",
help="DAG forward layers. Default=5",
type=int,
default=5,
)
args = parser.parse_args()
layers = [[] for _ in range(args.layers)]
edges = {}
node_index = -1
print(f"Creating {len(layers)} layers graph")
# Random horizontal connections -low probability-
def random_horizontal(layer):
for node1 in layer:
# Avoid cycles
for node2 in filter(
lambda n2: node1 != n2 and node1 not in map(lambda el: el[0], edges[n2]),
layer,
):
if random.randint(0, 100) < 10:
w = random.randint(1, 10)
edges[node1].append((node2, w))
# Connect two layers
def connect(layer1, layer2):
random_horizontal(layer1)
for node1 in layer1:
for node2 in layer2:
if random.randint(0, 100) < 30:
w = random.randint(1, 10)
edges[node1].append((node2, w))
# Start nodes 1 to 3
start_nodes = random.randint(1, 3)
start_layer = []
for sn in range(start_nodes + 1):
node_index += 1
start_layer.append(node_index)
# Gen nodes
for layer in layers:
nodes = random.randint(2, 5)
for n in range(nodes):
node_index += 1
layer.append(node_index)
# Connect all
layers.insert(0, start_layer)
for layer in layers:
for node in layer:
edges[node] = []
for i, layer in enumerate(layers[:-1]):
connect(layer, layers[i + 1])
# Print in DOT language
print("digraph {")
for node_key in [node_key for node_key in edges.keys() if len(edges[node_key]) > 0]:
for node_dst, weight in edges[node_key]:
print(f" {node_key} -> {node_dst} [label={weight}];")
print("}")
print("---- Adjacency list ----")
print(edges)
If you want to build a random DAG with N nodes and M (directed) edges, here's my solution:
import networkx as nx
import random
import matplotlib.pyplot as plt
random.seed(1134)
N_nodes = 10
N_edges = 15
def random_tree(N):
'''
Create a connected random tree with N nodes.
Edges are not directed.
Nodes are numbers from 0 to N-1.
Return a list of pairs (i,j), each one represents an edge.
'''
nodes = [0]
edges = list()
for i in range(1, N):
j = random.choice(nodes)
edges.append((i,j))
nodes.append(i)
return edges
def add_random_edges(N, M):
'''
N: number of nodes (index pool)
M: edges to append
'''
edges = list()
while M>0:
i = random.randint(0, N-1)
j = random.randint(0, N-1)
if i==j:
continue
M -= 1
edges.append((i,j))
return edges
def reshuffle(edges, N):
d = dict()
avail = [ i for i in range(N) ]
for i in range(N):
pos = random.randint(0, len(avail)-1)
r = avail[pos]
d[i] = r
avail[pos] = avail[-1]
avail.pop()
return [ (d[i], d[j]) for i,j in edges ]
def make_direct_dag(edges):
ordered = list()
for i,j in edges:
a = min(i,j)
b = max(i,j)
ordered.append((a,b))
return ordered
def random_connected_dag(N, M):
'''
Creates an unbiased random Directed Acyclic Graph with N vertice and M edges,
which is connected. There might be parallel edges, but there are not
self-loops or directed cycles, otherwise it wouldn't be a DAG.
N: number of vertices
M: number of edges
'''
assert M >= N-1
# create a random tree (of course connectec)
edges = random_tree(N)
M -= (N-1) # remaining edges
# add the rest of the edges at random
edges += add_random_edges(N, M)
# remove bias by reshufling node indexes
edges = reshuffle(edges, N)
# use the index of the nodes as the topological order
edges = make_direct_dag(edges)
return edges
def show_dag(dag):
G = nx.MultiDiGraph(dag)
for layer, nodes in enumerate(nx.topological_generations(G)):
for node in nodes:
G.nodes[node]['layer'] = layer
pos = nx.multipartite_layout(G, subset_key = 'layer')
fig, ax = plt.subplots()
nx.draw_networkx(G, pos = pos, ax = ax)
ax.set_title('Random DAG in topological order')
fig.tight_layout()
plt.show()
dag = random_connected_dag(N_nodes, N_edges)
show_dag(dag)
© 2022 - 2024 — McMap. All rights reserved.
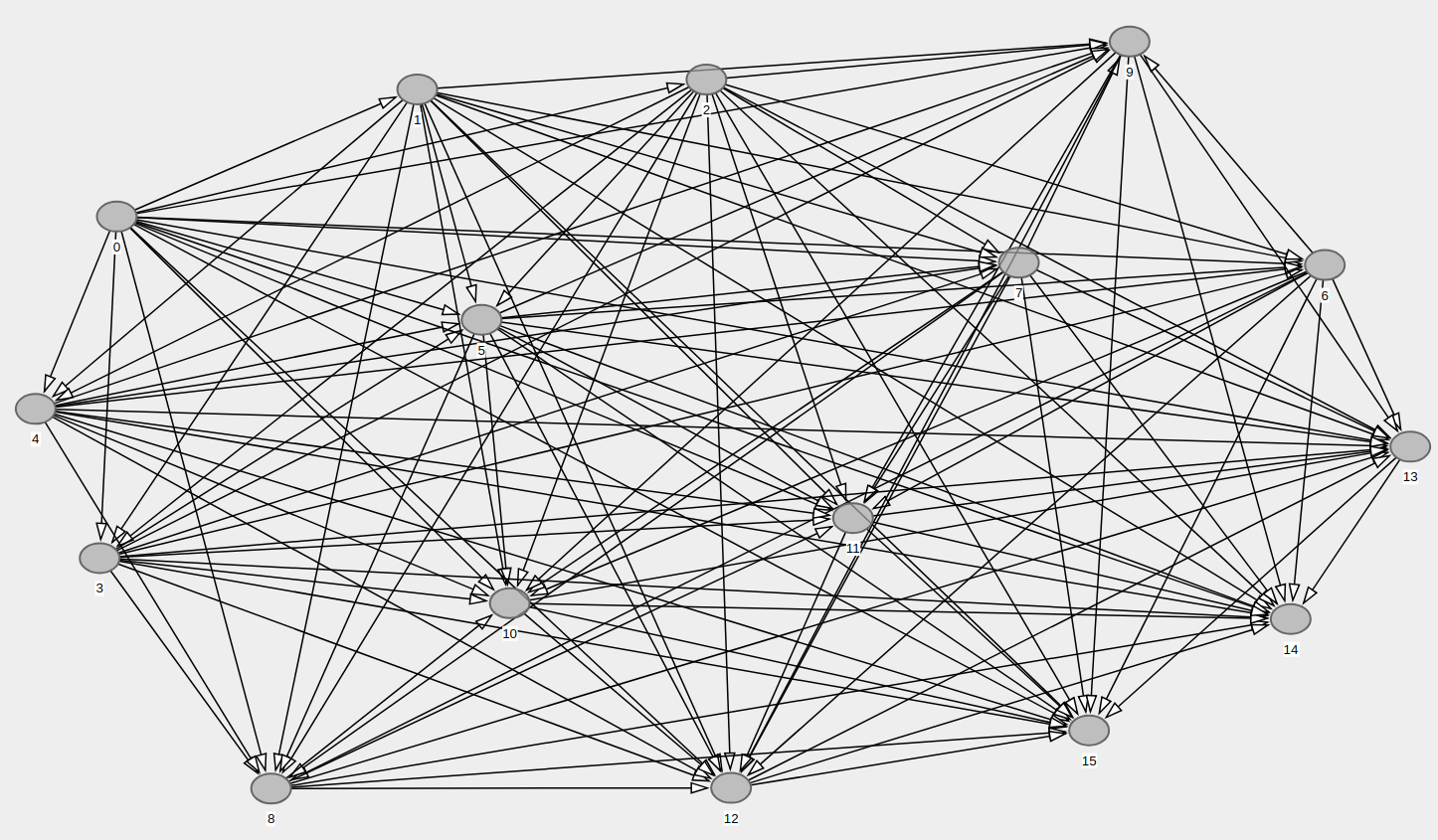
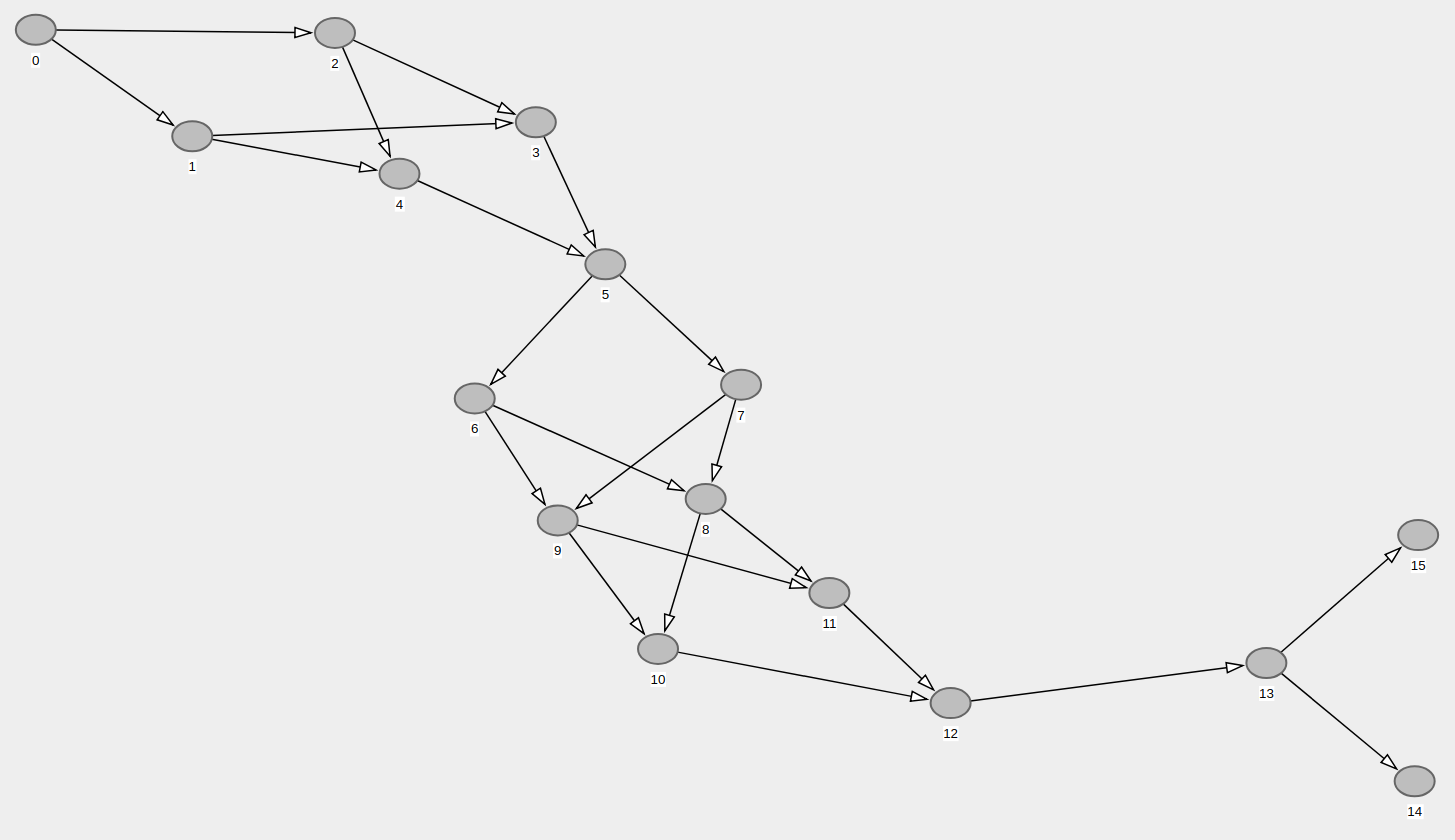
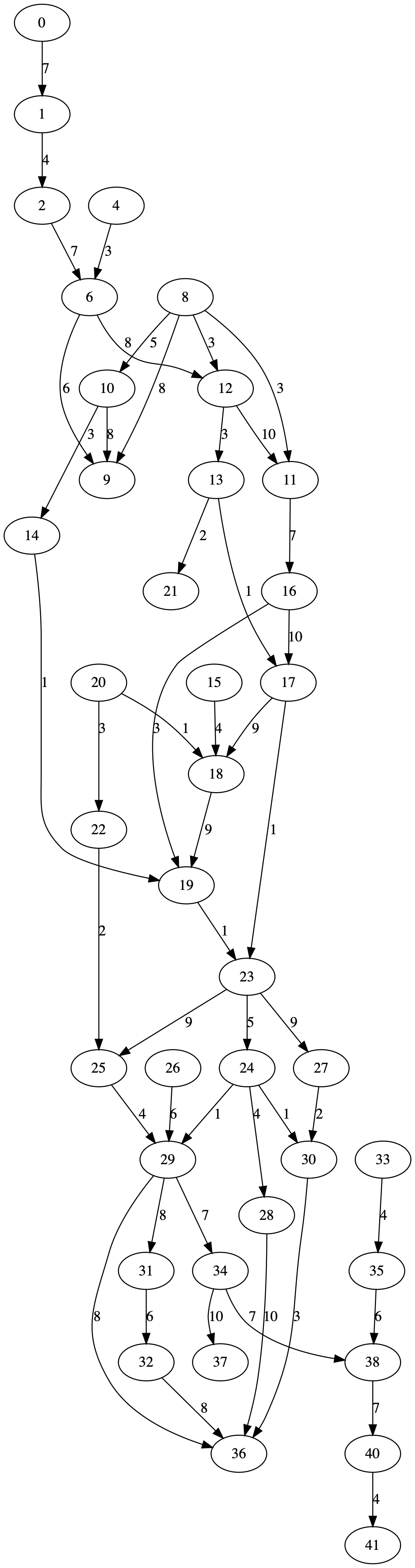
directed_acyclic_graphhere: condor.depaul.edu/rjohnson/source/graph_ge.c – Dornick