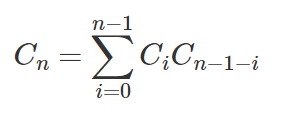The possible number of binary search trees that can be created with N keys is given by the Nth catalan number. Why?

Question

This has been bothering me for a while. I know that given N keys to arrange in the form of a binary search tree, the possible number of trees that can be created correspond to the Nth number from the Catalan sequence.

I have been trying to determine why this is; unable to find anything that might even attempt to explain it intuitively I resort to the collective knowledge of SO. I found other ways to calculate the number of possible trees, but they seemed less intuitive and no explanation was offered beyond how to use it. Plus the wiki page (that link above) even shows an image of the possible tree formations with 3 keys, which would lead me to think there's a nice and neat explanation to be heard (which is, needless to say, not included in the article).

Thanks in advance!

Johnjohna

Very interesting question, though I'm not sure it's really programming-related :-/ Seems like more of an abstract math (topology) thing. – Grant

Uh, this has nothing to do with topology! – Maremma

@Sergio: What is your question? Are you wondering why the number of binary search trees with N keys is the same as any of the quantities shown on that page to be Catalan numbers, or are you wondering about the expression for Catalan numbers themselves (which is proved on the page in four ways)? – Maremma

I'm wondering how to determine the number of possible BSTs that can be created given a number N of nodes. I discovered that the answer to that question is the same as asking "What's the Nth number in the catalan sequence?", but even though the formula is readily available on that wiki article, I'd like an explanation of why it works. I don't like to accept methods without some explanation of their inner logic or some basic, intuitive description other than a formula. – Johnjohna

This applies to binary trees in general, it has nothing to do with the specifics of search trees. – Walkout

@starblue: you're quite wrong – Boon

Just FYI - Related link: codingworkout.blogspot.com/2014/08/… – Beverie

Answer 1

Since there are four proofs in the wikipedia article you referenced, it seems you aren't looking for a mathematical explanation for the correspondence between the Catalan numbers and the permutations of a binary tree.

So instead, here are two ways to try and intuitively visualise how the Catalan sequence (1, 2, 5, 14, 42, ...) arises in combinatorial systems.

Dicing polygons into triangles

For a polygon of side N, how many ways can you draw cuts between the vertices that chop the polygon up entirely into triangles?

• Triangle (N=3): 1 (It's already a triangle)
• Square (N=4): 2 (Can slice at either diagonal)
• Pentagon (N=5): 5 (Two slicing lines emanating from a vertex. Five vertices to choose from)
• Hexagon (N=6): 14 (Try drawing it)
• ...and so on.

Drawing a path through a grid without crossing the diagonal

In this case, the number of unique paths is the Catalan number.

2x2 grid => 2 paths

  _|       |
_|       __|

3x3 grid => 5 paths

    _|       |       _|         |         |
  _|      _ _|      |          _|         |
_|      _|       _ _|      _ _|      _ _ _|

4x4 grid => 14 paths
5x5 grid => 42 paths

and so on.

If you try drawing the possible binary trees for a given N, you will see that the way the tree permutes is just the same.

Your desire not to just blindly accept the correspondence between the tree and the sequence is admirable. Unfortunately, it's difficult to go much further with this discussion (and explain why the Catalan formula 'happens to be' the way it is) without invoking binomial mathematics. The Wikipedia discussion of binomial coefficients is a good starting point if you want to understand combinatorics (which includes permutation counting) itself in more depth.

Straiten

Coming from a "Math Atheist",nice answer. flickr.com/photos/99706190@N00/1869299 – Poling

Answer 2

catalan http://www.nohre.se/publicImages/catalan.png

Any binary search tree can be encoded by visiting all nodes pre-order and encode a 1 for every parent and a 0 for every leaf. If the tree has n parents it will have n+1 leafs and consequently the binary code will have n 1:s and (n+1) 0:s. Moreover, and any prefix of the code will have at least as many 1:s as it has 0:s. Therefore, the number of possible trees equals the number of paths below the diagonal.

Rangoon

If you don't prove that there is one-to-one correspondence between trees and their binary encoding your argument is useless. – Somewise

Umm, you're using preorder in your example! – Pertinacious

Answer 3

Well here is the recursive solution to count the trees...

int countTrees(int numkeys){

if(numkeys > 1){
    int i =1;
    int sum=0;

    for(i = 1; i <= numkeys; i++){

        int lcount = countTrees(i-1);
        int rcount = countTrees(numkeys-i);
        sum += lcount*rcount;
    }
    return(sum);
}else
    return(1);
}

Fid

Answer 4

I have same desire to know why it happens to be the Catalan number; Just forget about what Catalan number is for now and find out the formula to calculate the number of unique binary trees for n nodes.

Let C(n) be the number of possible binary trees with given n vertices, C(0) = 1, now consider C(n) when n > 0, since there must be a root node for every binary tree, so the problem now turns to be how many possible binary trees we can generate on both left and right child of the root node with n – 1 vertices.

To find the answer, we have to enumerate all possible trees on both sides.

C(n) = C(0) * C(n - 1) + C(1) * C(n - 2) + ... + C(n – 2) * C(1) + C(n - 1) * C(0)

And that's the recursion form of the Catalan numbers. It's easy to accept it once I see this recursion form instead the formula in Wikipedia.

(Most of texts from https://coldfunction.com/mgen/p/3r)

Hamamelidaceous