How to increase the size of an axis (stretch) in a 3D Plot

Question

I have this so far:

x,y,z = data.nonzero()    
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, zdir='z', c= 'red')
plt.savefig("plot.png")

Which creates:

What I'd like to do is stretch this out to make the Z axis 9 times taller and keep X and Y the same. I'd like to keep the same coordinates though.

So far I tried this guy:

fig = plt.figure(figsize=(4.,35.))

But that just stretches out the plot.png image.

Poppy

Have you tried set_zlim(z_min, z_max)? Or set_zlim3d? – Bloomy

Thanks for the suggestion. what does zlim do? I'm not sure what I would put for z_min, and z_max. I'm happy with the z bounds it has, I just want it stretched. – Poppy

I misunderstood. Looks like you want to change the 3d aspect ratio. Doing this depends on the version of matplotlib you're working with. Try looking here1 or here2 – Bloomy

Thanks. I guess I don't understand what the here1 link would do. It seems like it wouldn't set the aspect ratio. I read here2 before asking this question but I can't see how to apply the answers to my code. – Poppy

The here1 accepted answer modifies the aspect ratio of the axis. It is a hack so you would need to modify matplotlib's files. It doesn't seem to allow different aspect ratios by default. – Amaro

There is a one-liner solution to this. A very simple monkey patch which requires adding only one line to your code. Check out my answer below: https://mcmap.net/q/418308/-how-to-increase-the-size-of-an-axis-stretch-in-a-3d-plot – Bowing

Answer 1

The code example below provides a way to scale each axis relative to the others. However, to do so you need to modify the Axes3D.get_proj function. Below is an example based on the example provided by matplot lib: http://matplotlib.org/1.4.0/mpl_toolkits/mplot3d/tutorial.html#line-plots

(There is a shorter version at the end of this answer)

from mpl_toolkits.mplot3d.axes3d import Axes3D
from mpl_toolkits.mplot3d import proj3d

import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt

#Make sure these are floating point values:                                                                                                                                                                                              
scale_x = 1.0
scale_y = 2.0
scale_z = 3.0

#Axes are scaled down to fit in scene                                                                                                                                                                                                    
max_scale=max(scale_x, scale_y, scale_z)

scale_x=scale_x/max_scale
scale_y=scale_y/max_scale
scale_z=scale_z/max_scale

#Create scaling matrix                                                                                                                                                                                                                   
scale = np.array([[scale_x,0,0,0],
                  [0,scale_y,0,0],
                  [0,0,scale_z,0],
                  [0,0,0,1]])
print scale

def get_proj_scale(self):
    """                                                                                                                                                                                                                                    
    Create the projection matrix from the current viewing position.                                                                                                                                                                        

    elev stores the elevation angle in the z plane                                                                                                                                                                                         
    azim stores the azimuth angle in the x,y plane                                                                                                                                                                                         

    dist is the distance of the eye viewing point from the object                                                                                                                                                                          
    point.                                                                                                                                                                                                                                 

    """
    relev, razim = np.pi * self.elev/180, np.pi * self.azim/180

    xmin, xmax = self.get_xlim3d()
    ymin, ymax = self.get_ylim3d()
    zmin, zmax = self.get_zlim3d()

    # transform to uniform world coordinates 0-1.0,0-1.0,0-1.0                                                                                                                                                                             
    worldM = proj3d.world_transformation(
        xmin, xmax,
        ymin, ymax,
        zmin, zmax)

    # look into the middle of the new coordinates                                                                                                                                                                                          
    R = np.array([0.5, 0.5, 0.5])

    xp = R[0] + np.cos(razim) * np.cos(relev) * self.dist
    yp = R[1] + np.sin(razim) * np.cos(relev) * self.dist
    zp = R[2] + np.sin(relev) * self.dist
    E = np.array((xp, yp, zp))

    self.eye = E
    self.vvec = R - E
    self.vvec = self.vvec / proj3d.mod(self.vvec)

    if abs(relev) > np.pi/2:
    # upside down                                                                                                                                                                                                                          
      V = np.array((0, 0, -1))
    else:
      V = np.array((0, 0, 1))
    zfront, zback = -self.dist, self.dist

    viewM = proj3d.view_transformation(E, R, V)
    perspM = proj3d.persp_transformation(zfront, zback)
    M0 = np.dot(viewM, worldM)
    M = np.dot(perspM, M0)

    return np.dot(M, scale);

Axes3D.get_proj=get_proj_scale

"""
You need to include all the code above.
From here on you should be able to plot as usual.
"""

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure(figsize=(5,5))
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)
ax.plot(x, y, z, label='parametric curve')
ax.legend()

plt.show()

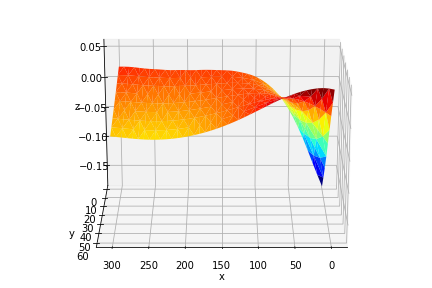
Standard output:

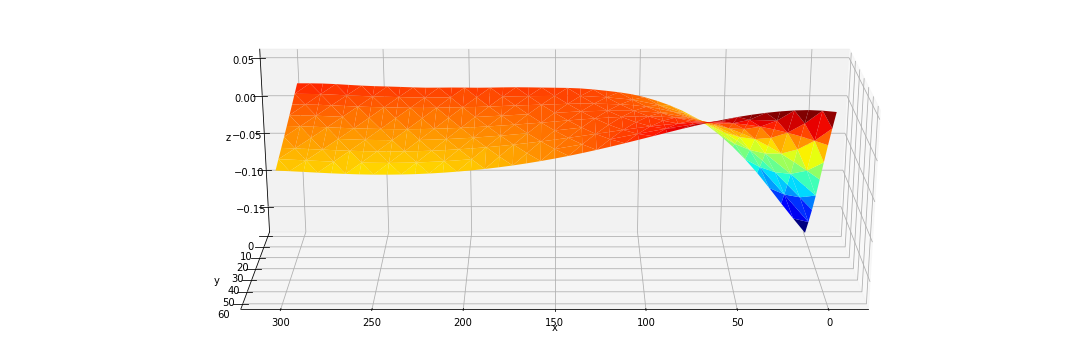
Scaled by (1, 2, 3):

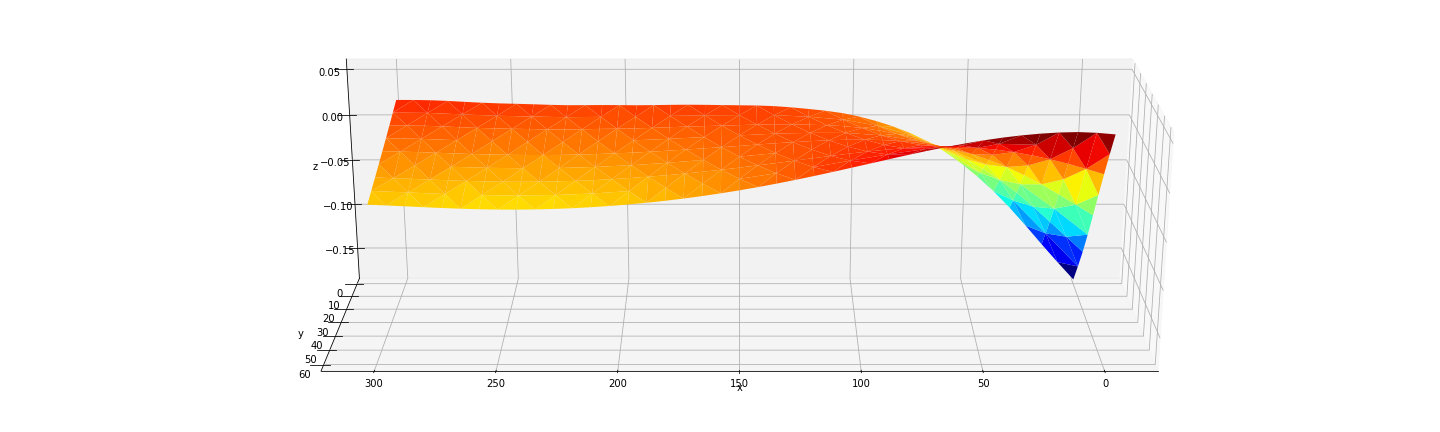
Scaled by (1, 1, 3):

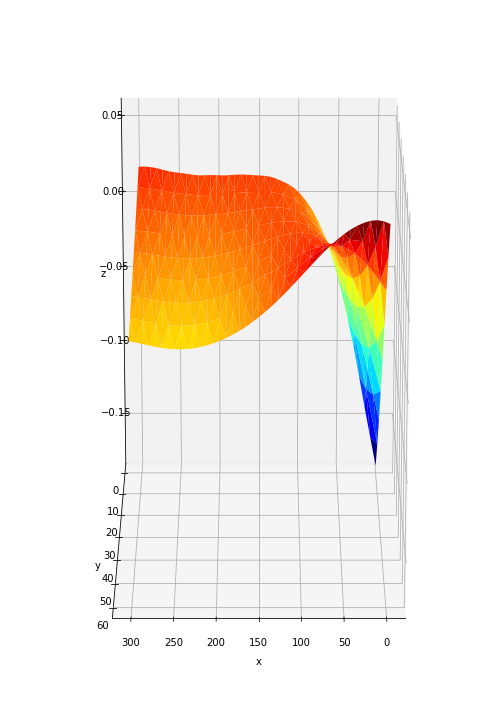
The reason I particularly like this method, Swap z and x, scale by (3, 1, 1):

Below is a shorter version of the code.

from mpl_toolkits.mplot3d.axes3d import Axes3D
from mpl_toolkits.mplot3d import proj3d

import matplotlib as mpl
import numpy as np
import matplotlib.pyplot as plt

mpl.rcParams['legend.fontsize'] = 10

fig = plt.figure(figsize=(5,5))
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)


"""                                                                                                                                                    
Scaling is done from here...                                                                                                                           
"""
x_scale=1
y_scale=1
z_scale=2

scale=np.diag([x_scale, y_scale, z_scale, 1.0])
scale=scale*(1.0/scale.max())
scale[3,3]=1.0

def short_proj():
  return np.dot(Axes3D.get_proj(ax), scale)

ax.get_proj=short_proj
"""                                                                                                                                                    
to here                                                                                                                                                
"""

ax.plot(z, y, x, label='parametric curve')
ax.legend()

plt.show()

Cuba

@gboffi I can. You should be able to simply copy the code and run it. – Cuba

hah, beat me too it. I think this is the way to do it though. You can check out the default scaling, world_transformation(), here – Carpophagous

The one limitation is that it requires the data to be centred. Otherwise, the dot product will also create a spatial transformation of the figure which may shift it off the screen – Pushball

I found the result plot is always so zoomed out using this solution. – Overzealous

Answer 2

Please note that the answer below simplifies the patch, but uses the same underlying principle as the answer by @ChristianSarofeen.

Solution

As already indicated in other answers, it is not a feature that is currently implemented in matplotlib. However, since what you are requesting is simply a 3D transformation that can be applied to the existing projection matrix used by matplotlib, and thanks to the wonderful features of Python, this problem can be solved with a simple oneliner:

ax.get_proj = lambda: np.dot(Axes3D.get_proj(ax), np.diag([scale_x, scale_y, scale_z, 1]))

where scale_x, scale_y and scale_z are values from 0 to 1 that will re-scale your plot along each of the axes accordingly. ax is simply the 3D axes which can be obtained with ax = fig.gca(projection='3d')

Explanation

To explain, the function get_proj of Axes3D generates the projection matrix from the current viewing position. Multiplying it by a scaling matrix:

scale_x, 0,       0
0,       scale_y, 0
0,       0,       scale_z
0,       0,       1

includes the scaling into the projection used by the renderer. So, what we are doing here is substituting the original get_proj function with an expression taking the result of the original get_proj and multiplying it by the scaling matrix.

Example

To illustrate the result with the standard parametric function example:

from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.gca(projection='3d')
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z ** 2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)

# OUR ONE LINER ADDED HERE:
ax.get_proj = lambda: np.dot(Axes3D.get_proj(ax), np.diag([0.5, 0.5, 1, 1]))

ax.plot(x, y, z)
plt.show()

for values 0.5, 0.5, 1, we get:

while for values 0.2, 1.0, 0.2, we get:

Bowing

Answer 3

In my case I wanted to stretch z-axis 2 times for better point visibility

from mpl_toolkits import mplot3d
from mpl_toolkits.mplot3d import Axes3D

import matplotlib.pyplot as plt
# plt.rcParams["figure.figsize"] = (10,200)
# plt.rcParams["figure.autolayout"] = True
ax = plt.axes(projection='3d')
ax.set_box_aspect(aspect = (1,1,2))

ax.plot(dataX,dataY,dataZ)

Crudity

I believe it's the best modern answer, apparently nowadays you don't need nothing else, this works like a charm! – Acuminate

As of 2024, this works significantly better than the other answers on this question. – Hexone

Answer 4

I looks like by default, mplot3d will leave quite a bit of room at the top and bottom of a very tall plot. But, you can trick it into filling that space using fig.subplots_adjust, and extending the top and bottom out of the normal plotting area (i.e. top > 1 and bottom < 0). Some trial and error here is probably needed for your particular plot.

I've created some random arrays for x, y, and z with limits similar to your plot, and have found the parameters below (bottom=-0.15, top = 1.2) seem to work ok.

You might also want to change ax.view_init to set a nice viewing angle.

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from numpy import random

# Make some random data with similar limits to the OP's example
x,y,z=random.rand(3,100)
z*=250
y*=800
y+=900
x*=350
x+=1200

fig=plt.figure(figsize=(4,35))

# Set the bottom and top outside the actual figure limits, 
# to stretch the 3D axis
fig.subplots_adjust(bottom=-0.15,top=1.2)

ax = fig.add_subplot(111, projection='3d')

# Change the viewing angle to an agreeable one
ax.view_init(2,None)

ax.scatter(x, y, z, zdir='z', c= 'red')
plt.savefig("plot.png")

Rondon

I don't like this option as you're really just skewing the viewport. You can tell when you try to rotate this plot that the image is really just getting skewed. – Cuba

Answer 5

Sounds like you're trying to adjust the scale of the plot. I don't think there's a way to stretch a linear scale to user specifications, but you can use set_yscale(), set_xscale(), set_zscale() to alter the scales with respect to each other.

Intuitively, set_yscale(log), set_xscale(log), set_zscale(linear) might solve your problems.

A likely better option: specify a stretch, set them all to symlog with the same log base and then specify the Z-axis's symlog scale with the linscalex/linscaley kwargs to your specifications.

More here:

http://matplotlib.org/mpl_toolkits/mplot3d/api.html

Goodbye

Answer 6

I found this while searching on a similar problem. After experimenting a bit, perhaps I can share some of my prelim findings here..matplotlib library is VAST!! (am a newcomer). Note that quite akin to this question, all i wanted was to 'visually' stretch the chart without distorting it.

Background story (only key code snippets are shown to avoid unnecessary clutter for those who know the library, and if you want a run-able code please drop a comment): I have three 1-d ndarrays representing the X,Y and Z data points respectively. Clearly I can't use plot_surface (as it requires 2d ndarrays for each dim) so I went for the extremely useful plot_trisurf:

fig = plt.figure()
ax = Axes3D(fig)
3d_surf_obj = ax.plot_trisurf(X, Y, Z_defl, cmap=cm.jet,linewidth=0,antialiased=True)

You can think of the plot like a floating barge deforming in waves...As you can see, the axes stretch make it pretty deceiving visually (note that x is supposed to be at x6 times longer than y and >>>>> z). While the plot points are correct, I wanted something more visually 'stretched' at the very least. Was looking for A QUICK FIX, if I may. Long story cut short, I found a bit of success with...'figure.figsize' general setting (see snippet below).

    matplotlib.rcParams.update({'font.serif': 'Times New Roman',
                                'font.size': 10.0,
                                'axes.labelsize': 'Medium',
                                'axes.labelweight': 'normal',
                                'axes.linewidth': 0.8,
                                 ###########################################
                                 # THIS IS THE IMPORTANT ONE FOR STRETCHING
                                 # default is [6,4] but...i changed it to
                                'figure.figsize':[15,5]   # THIS ONE #
                              })

For [15,5] I got something like...

Pretty neat!!

So I started to push it.... and got up to [20,6] before deciding to settle there..

If you want to try for visually stretching the vertical axis, try with ratios like... [7,10], which in this case gives me ...

Not too shabby !

Should do it for visual prowess.

Swirly

I copied your example, but unfortunately doesn't work – Peipeiffer

Hi @Peipeiffer , could you elaborate on what exactly doesn't work / your error encountered ? I'd be happy to help – Swirly

Answer 7

Multiply all your z values by 9,

ax.scatter(x, y, 9*z, zdir='z', c= 'red')

And then give the z-axis custom plot labels and spacing.

ax.ZTick = [0,-9*50, -9*100, -9*150, -9*200];
ax.ZTickLabel = {'0','-50','-100','-150','-200'};

Trophy

This won't make the Z-Axis taller. – Cuba