How to implement depth first search for graph with a non-recursive approach

Question

I have spent lots of time on this issue. However, I can only find solutions with non-recursive methods for a tree: Non recursive for tree, or a recursive method for the graph, Recursive for graph.

And lots of tutorials (I don't provide those links here) don't provide the approaches as well. Or the tutorial is totally incorrect. Please help me.

Updated:

It's really hard to describe:

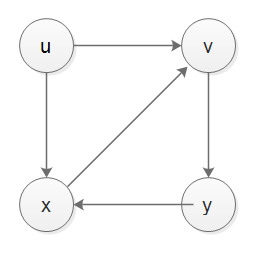
If I have an undirected graph:

   1
 / |  \
4  |   2
    3 /

1-- 2-- 3 --1 is a cycle.

At the step: 'push the neighbors of the popped vertex into the stack', what's the order in which the vertices should be pushed?

If the pushed order is 2, 4, 3, the vertices in the stack are:

| |
|3|
|4|
|2|    
 _

After popping the nodes, we get the result: 1 -> 3 -> 4 -> 2 instead of 1--> 3 --> 2 -->4.

It's incorrect. What condition should I add to stop this scenario?

Delija

Using the algorithm in @amit's excellent answer, I cannot get 4 to appear between 3 and 2. There is one important detail in the algorithm. A node is added to the visited set only when it is actually visited, not when it is pushed on the stack. Marking it visited on stack push would result in the problem you are getting, by preventing treating 3 as a child of 2, or 2 as a child of 3. – Harakiri

Answer 1

A DFS without recursion is basically the same as BFS - but use a stack instead of a queue as the data structure.

The thread Iterative DFS vs Recursive DFS and different elements order handles with both approaches and the difference between them (and there is! you will not traverse the nodes in the same order!)

The algorithm for the iterative approach is basically:

DFS(source):
  s <- new stack
  visited <- {} // empty set
  s.push(source)
  while (s is not empty):
    current <- s.pop()
    if (current is in visited):
        continue
    visited.add(current)
    // do something with current
    for each node v such that (current,v) is an edge:
        s.push(v)

Madox

Well, that thread didn't tell me the specific function implementation like: stack.Read(); Whatever, I want to know how to avoid cyclic problem, avoiding to add the same node duplicately AND as I add the neighbors of one node, the order of the nodes pushed into the stack is right so that as I pop them out, it can get correct order. – Delija

@Stallman visited keeps track of the visited nodes, so that you won't visit the same node twice. As for the order of iteration, if you have a specific order you can implement it by replacing the line for each node... with your order of iteration. +1 for a good answer! – Louettalough

I have to implement an executable code to make sure your pseudo-code is correct. Or you can provide specific source code to proof it. – Delija

Won't this code's space complexity use extra memory? I believe the best space complexity for iterative DFS is O(n). – Al

@BillCheng If you are referring to the extra visited set, you need it also in the recursive approach, unless you allocate extra memory for the state in the node objects themselves (and that will also be O(n) memory). DFS uses O(n) extra memory, regardless if it's recursive or iterative. – Madox

@Madox Your psuedo-code is correct and it has the same complexity as the recursive one (both in terms of time and space). However, your stack size can be $O(m)$ in worst case, that can be improved to $O(n)$. – Annmarie

This code is O(n²) for space and time. Consider a complete graph (where every vertex is connected to every other vertex). For all n vertices, every iteration of the while loop will add another list of n vertices to the stack, so there will be O(n²) iterations in total. The space grows a bit slower due of the popping of visited vertices, but it is still O(n²) because it grows as the arithmetic series n+(n-1)+(n-2)+...+2+1. Try this example code. – Eu

I've posted Python code with reduced complexity in a comment below. It follows the same concept as this other answer by using the stack to emulate the function call stack of a recursive DFS. – Eu

I think the biggest problem with this approach is that it's essentially a pre-order DFS. Cannonically, the visit state of in DFS is by color (white/gray/black) for many purposes, including detecting cycle in directed graph. Your algo is fine for undirected graph since not all three visiting states are needed for undirected graph. In case of directed graph, a more complicated DFS is needed in order to mark the node's color to black post order. – Usk

@Usk Note that I referred to this issue explicitly and pointed to this thread in the answer for this purpose. – Madox

how to calculate pre-visit and post-visit ids in this iterative version. Can the size of the stack be used as the depth of the node on top of the stack? – Sender

Answer 2

This is not an answer, but an extended comment, showing the application of the algorithm in @amit's answer to the graph in the current version of the question, assuming 1 is the start node and its neighbors are pushed in the order 2, 4, 3:

               1
             / |  \
            4  |   2
               3 /

Actions            Stack             Visited
=======            =====             =======
push 1             [1]               {}
pop and visit 1    []                {1}
 push 2, 4, 3      [2, 4, 3]         {1}
pop and visit 3    [2, 4]            {1, 3}
 push 1, 2         [2, 4, 1, 2]      {1, 3}
pop and visit 2    [2, 4, 1]         {1, 3, 2}
 push 1, 3         [2, 4, 1, 1, 3]   {1, 3, 2}
pop 3 (visited)    [2, 4, 1, 1]      {1, 3, 2}
pop 1 (visited)    [2, 4, 1]         {1, 3, 2}
pop 1 (visited)    [2, 4]            {1, 3, 2}
pop and visit 4    [2]               {1, 3, 2, 4}
  push 1           [2, 1]            {1, 3, 2, 4}
pop 1 (visited)    [2]               {1, 3, 2, 4}
pop 2 (visited)    []                {1, 3, 2, 4}

Thus applying the algorithm pushing 1's neighbors in the order 2, 4, 3 results in visit order 1, 3, 2, 4. Regardless of the push order for 1's neighbors, 2 and 3 will be adjacent in the visit order because whichever is visited first will push the other, which is not yet visited, as well as 1 which has been visited.

Harakiri

Great explanation. I can't mark this as the answer since no source code is provided. – Delija

why push the visited nodes ? – Geophyte

@Shiro A node may become visited while it is on the stack, so the check for visited during pop is unavoidable. See not 2 in the example. You could also check during push, but it is not necessary to do so. – Harakiri

@Shiro How would you change the algorithm? – Harakiri

@Shiro The cost of doing that is an additional conditional branch. Conditional branches can be very expensive through causing a pipeline flush. It is far from obvious that the savings of a simple stack push-pop will cover the cost of the branch, and adding it makes the algorithm more complicated than it needs to be. – Harakiri

Let us continue this discussion in chat. – Harakiri

You check for visited nodes at pop. I say we should check for visited nodes at push. My way is better because the earlier we check, the less items we have on the visited nodes collection, so its faster, and also we use less memory for the stack. The amount of pop calls is equal to the amount of push calls. I am not adding any complexity. Look at your own example. – Geophyte

With my code the stack's max size is 48.192. With your algorithm my stack max size 326.663. The graph is 4.7 million nodes (Greece car graph). Both algorithms have the same results. – Geophyte

Also, my code is about 15% faster. 210ms vs 250ms. Here is an updated version of my code – Geophyte

@Shiro I suggest putting your comments on the actual answer that gave the algorithm. – Harakiri

Answer 3

The DFS logic should be:

1) if the current node is not visited, visit the node and mark it as visited
2) for all its neighbors that haven't been visited, push them to the stack

For example, let's define a GraphNode class in Java:

class GraphNode {
    int index;
    ArrayList<GraphNode> neighbors;
}

and here is the DFS without recursion:

void dfs(GraphNode node) {
    // sanity check
    if (node == null) {
        return;
    }

    // use a hash set to mark visited nodes
    Set<GraphNode> set = new HashSet<GraphNode>();

    // use a stack to help depth-first traversal
    Stack<GraphNode> stack = new Stack<GraphNode>();
    stack.push(node);

    while (!stack.isEmpty()) {
        GraphNode curr = stack.pop();

        // current node has not been visited yet
        if (!set.contains(curr)) {
            // visit the node
            // ...

            // mark it as visited
            set.add(curr);
        }

        for (int i = 0; i < curr.neighbors.size(); i++) {
            GraphNode neighbor = curr.neighbors.get(i);

            // this neighbor has not been visited yet
            if (!set.contains(neighbor)) {
                stack.push(neighbor);
            }
        }
    }
}

We can use the same logic to do DFS recursively, clone graph etc.

Disarticulate

Answer 4

Many people will say that non-recursive DFS is just BFS with a stack rather than a queue. That's not accurate, let me explain a bit more.

Recursive DFS

Recursive DFS uses the call stack to keep state, meaning you do not manage a separate stack yourself.

However, for a large graph, recursive DFS (or any recursive function that is) may result in a deep recursion, which can crash your problem with a stack overflow (not this website, the real thing).

Non-recursive DFS

DFS is not the same as BFS. It has a different space utilization, but if you implement it just like BFS, but using a stack rather than a queue, you will use more space than non-recursive DFS.

Why more space?

Consider this:

// From non-recursive "DFS"
for (auto i&: adjacent) {
    if (!visited(i)) {
        stack.push(i);
    }
}

And compare it with this:

// From recursive DFS
for (auto i&: adjacent) {
    if (!visited(i)) {
        dfs(i);
    }
}

In the first piece of code you are putting all the adjacent nodes in the stack before iterating to the next adjacent vertex and that has a space cost. If the graph is large it can make a significant difference.

What to do then?

If you decide to solve the space problem by iterating over the adjacency list again after popping the stack, that's going to add time complexity cost.

One solution is to add items to the stack one by one, as you visit them. To achieve this you can save an iterator in the stack to resume the iteration after popping.

Lazy way

In C/C++, a lazy approach is to compile your program with a larger stack size and increase stack size via ulimit, but that's really lousy. In Java you can set the stack size as a JVM parameter.

Tiro

Answer 5

Recursion is a way to use the call stack to store the state of the graph traversal. You can use the stack explicitly, say by having a local variable of type std::stack, then you won't need the recursion to implement the DFS, but just a loop.

Calyx

Yes, I tried to use stack, but I don't know how to avoid cyclic problem. – Delija

Answer 6

okay. if you are still looking for a java code

dfs(Vertex start){
    Stack<Vertex> stack = new Stack<>(); // initialize a stack
    List<Vertex> visited = new ArrayList<>();//maintains order of visited nodes
    stack.push(start); // push the start
    while(!stack.isEmpty()){ //check if stack is empty
        Vertex popped = stack.pop(); // pop the top of the stack
        if(!visited.contains(popped)){ //backtrack if the vertex is already visited
            visited.add(popped); //mark it as visited as it is not yet visited
            for(Vertex adjacent: popped.getAdjacents()){ //get the adjacents of the vertex as add them to the stack
                    stack.add(adjacent);
            }
        }
    }

    for(Vertex v1 : visited){
        System.out.println(v1.getId());
    }
}

Dilly

You should have explained the code a bit... OP should understand how the code works... Giving plain code is much like doing their homework... – Siegfried

hmmm i get it. make sense. – Dilly

Answer 7

Python code. The time complexity is O(V+E) where V and E are the number of vertices and edges respectively. The space complexity is O(V) due to the worst-case where there is a path that contains every vertex without any backtracking (i.e. the search path is a linear chain).

The stack stores tuples of the form (vertex, vertex_edge_index) so that the DFS can be resumed from a particular vertex at the edge immediately following the last edge that was processed from that vertex (just like the function call stack of a recursive DFS).

The example code uses a complete digraph where every vertex is connected to every other vertex. Hence it is not necessary to store an explicit edge list for each node, as the graph is an edge list (the graph G contains every vertex).

numv = 1000
print('vertices =', numv)
G = [Vertex(i) for i in range(numv)]

def dfs(source):
  s = []
  visited = set()
  s.append((source,None))
  time = 1
  space = 0
  while s:
    time += 1
    current, index = s.pop()
    if index is None:
      visited.add(current)
      index = 0
    # vertex has all edges possible: G is a complete graph
    while index < len(G) and G[index] in visited:
      index += 1
    if index < len(G):
      s.append((current,index+1))
      s.append((G[index], None))
    space = max(space, len(s))
  print('time =', time, '\nspace =', space)

dfs(G[0])

Output:

time = 2000 
space = 1000

Note that time here is measuring V operations and not E. The value is numv*2 because every vertex is considered twice, once on discovery and once on finishing.

Eu

I came to stackoverflow to avoid a stack overflow. – Gine

Answer 8

Acutally, stack is not well able to deal with discover time and finish time, if we want to implement DFS with stack, and want to deal with discover time and finish time, we would need to resort to another recorder stack, my implementation is shown below, have test correct, below is for case-1, case-2 and case-3 graph.

from collections import defaultdict

class Graph(object):

    adj_list = defaultdict(list)

    def __init__(self, V):
        self.V = V

    def add_edge(self,u,v):
        self.adj_list[u].append(v)

    def DFS(self):
        visited = []
        instack = []
        disc = []
        fini = []
        for t in range(self.V):
            visited.append(0)
            disc.append(0)
            fini.append(0)
            instack.append(0)

        time = 0
        for u_ in range(self.V):
            if (visited[u_] != 1):
                stack = []
                stack_recorder = []
                stack.append(u_)
                while stack:
                    u = stack.pop()
                    visited[u] = 1
                    time+=1
                    disc[u] = time
                    print(u)
                    stack_recorder.append(u)
                    flag = 0
                    for v in self.adj_list[u]:
                        if (visited[v] != 1):
                            flag = 1
                            if instack[v]==0:
                                stack.append(v)
                            instack[v]= 1



                    if flag == 0:
                        time+=1
                        temp = stack_recorder.pop()
                        fini[temp] = time
                while stack_recorder:
                    temp = stack_recorder.pop()
                    time+=1
                    fini[temp] = time
        print(disc)
        print(fini)

if __name__ == '__main__':

    V = 6
    G = Graph(V)

#==============================================================================
# #for case 1
#     G.add_edge(0,1)
#     G.add_edge(0,2)
#     G.add_edge(1,3)
#     G.add_edge(2,1)
#     G.add_edge(3,2) 
#==============================================================================

#==============================================================================
# #for case 2
#     G.add_edge(0,1)
#     G.add_edge(0,2)
#     G.add_edge(1,3)
#     G.add_edge(3,2)  
#==============================================================================

#for case 3
    G.add_edge(0,3)    
    G.add_edge(0,1)

    G.add_edge(1,4)
    G.add_edge(2,4)
    G.add_edge(2,5)
    G.add_edge(3,1)
    G.add_edge(4,3)
    G.add_edge(5,5)    


    G.DFS()   

Fibroblast

Answer 9

I think you need to use a visited[n] boolean array to check if the current node is visited or not earlier.

Var

Answer 10

A recursive algorithm works very well for DFS as we try to plunge as deeply as we can, ie. as soon as we find an un-explored vertex, we're going to explore its FIRST un-explored neighbor right away. You need to BREAK out of the for loop as soon as you find the first un-explored neighbor.

for each neighbor w of v
   if w is not explored
       mark w as explored
       push w onto the stack
       BREAK out of the for loop

Loculus

when we reach the end of one path till the last depth, wouldn't the stack be empty if we don't really keep all neighbor in the stack at once? – Parthenope

Answer 11

I think this is an optimized DFS regarding space-correct me if I am wrong.

s = stack
s.push(initial node)
add initial node to visited
while s is not empty:
    v = s.peek()
    if for all E(v,u) there is one unvisited u:
        mark u as visited
        s.push(u)
    else 
        s.pop

Al

Answer 12

Using Stack and implementing as done by the call stack in the recursion process-

The Idea is to push a vertex in the stack, and then push its vertex adjacent to it which is stored in a adjacency list at the index of the vertex and then continue this process until we cannot move further in the graph, now if we cannot move ahead in the graph then we will remove the vertex which is currently on the top of the stack as it is unable to take us on any vertex which is unvisited.

Now, using stack we take care of the point that the vertex is only removed from the stack when all the vertices that can be explored from the current vertex have been visited, which was being done by the recursion process automatically.

for ex -

See the example graph here.

( 0 ( 1 ( 2 ( 4 4 ) 2 ) ( 3 3 ) 1 ) 0 ) ( 6 ( 5 5 ) ( 7 7 ) 6 )

The above parenthesis show the order in which the vertex is added on the stack and removed from the stack, so a parenthesis for a vertex is closed only when all the vertices that can be visited from it have been done.

(Here I have used the Adjacency List representation and implemented as a vector of list (vector > AdjList) by using C++ STL)

void DFSUsingStack() {
    /// we keep a check of the vertices visited, the vector is set to false for all vertices initially.
    vector<bool> visited(AdjList.size(), false);

    stack<int> st;

    for(int i=0 ; i<AdjList.size() ; i++){
        if(visited[i] == true){
            continue;
        }
        st.push(i);
        cout << i << '\n';
        visited[i] = true;
        while(!st.empty()){
            int curr = st.top();
            for(list<int> :: iterator it = AdjList[curr].begin() ; it != AdjList[curr].end() ; it++){
                if(visited[*it] == false){
                    st.push(*it);
                    cout << (*it) << '\n';
                    visited[*it] = true;
                    break;
                }
            }
            /// We can move ahead from current only if a new vertex has been added on the top of the stack.
            if(st.top() != curr){
                continue;
            }
            st.pop();
        }
    }
}

Langevin

Answer 13

The following Java Code will be handy:-

private void DFS(int v,boolean[] visited){
    visited[v]=true;
    Stack<Integer> S = new Stack<Integer>();
    S.push(v);
    while(!S.isEmpty()){
        int v1=S.pop();     
        System.out.println(adjLists.get(v1).name);
        for(Neighbor nbr=adjLists.get(v1).adjList; nbr != null; nbr=nbr.next){
             if (!visited[nbr.VertexNum]){
                 visited[nbr.VertexNum]=true;
                 S.push(nbr.VertexNum);
             }
        }
    }
}
public void dfs() {
    boolean[] visited = new boolean[adjLists.size()];
    for (int v=0; v < visited.length; v++) {
        if (!visited[v])/*This condition is for Unconnected Vertices*/ {

            System.out.println("\nSTARTING AT " + adjLists.get(v).name);
            DFS(v, visited);
        }
    }
}

Karlykarlyn