std::unordered_set has no O(1) random access in the sense of an array. It is possible to access an element, based on key, in O(1) but it is impossible to find the k-th element.
Despite that, here is a way to get a random element with a uniform distribution from std::unordered_map (or with std::unordered_set if the key has a mutable field). I have laid out a similar technique in an answer to SO question Data Structure(s) Allowing For Alteration Through Iteration and Random Selection From Subset (C++).
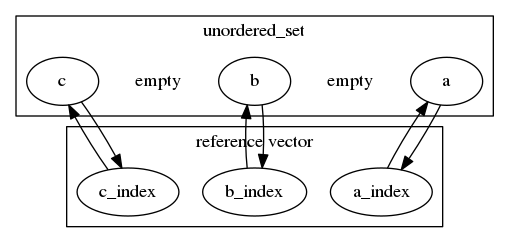
The idea is to supplement each entry in std::unordered_set with a mutable index value into a vector of pointers into the unordered_set. The size of the vector is the size of the unordered_set. Every time a new element is inserted to the unordered_set, a pointer to that element is push_back-ed into the vector. Every time an element is erased from the unordered_set, the corresponding entry in the vector is located in O(1), and is swapped with the back() element of the vector. The index of the previously back() element is amended, and now points to its new location in the vector. Finally the old entry is pop_back()-ed from the vector.
This vector points exactly to all elements in the unordered_set. It takes O(1) to pick a random element from the combined structure in uniform distribution. It takes O(1) to add or erase an element to the combined structure.
NOTE: Pointers to elements (unlike iterators) are guaranteed to stay valid as long as the element exists.
Here is how this should look:
![three elements in the set]()
For erasing element c:
- swap element c_index and a_index and fix the pointers to them:
- pop_back last element, which is element_c from the vector.
- erase c from the
unordered_set.
Randomization is trivial - simply select an element at random from the vector.
EDIT: Here is a partial code that can return a uniformly-distributed random element from an unordered_set. I had to do some things slightly different than in my explanations above, since there is no reliable indexing (or iterators) into unordered_set. The thing that makes it impossible to hold iterators into the unordered_set is that its elements are getting rehashed from time to time, invalidating all iterators in the process. So, instead of stable indexing, this solution is simply using pointers into an object that is never reallocated:
#include <unordered_set>
#include <functional>
#include <vector>
#include <memory>
#include <random>
template <class T>
class RandomUnorderedSet
{
private:
struct Entry {
Entry(const T & data_in, unsigned index_in_vector_in)
: data(data_in), index_in_vector(index_in_vector_in)
{}
T data;
unsigned index_in_vector;
};
struct PtrEntryHash {
auto operator()(const std::unique_ptr<Entry> & entry) const
{
return std::hash<T>()(entry->data);
}
};
struct PtrEntryEqual {
bool operator()(const std::unique_ptr<Entry> & a,
const std::unique_ptr<Entry> & b ) const
{
return a->data == b->data;
}
};
public:
bool insert(const T & element)
{
auto entry_ptr = std::make_unique<Entry>(element, m_entry_vector.size());
if (m_entry_set.count(entry_ptr) > 0)
return false;
m_entry_vector.push_back(entry_ptr.get());
try {
m_entry_set.insert(std::move(entry_ptr));
} catch(...) {
m_entry_vector.pop_back();
throw;
}
return true;
}
// Return the number of elements removed
int erase(const T & element)
{
auto it = m_entry_set.find(element);
if (it == m_entry_set.end())
return 0;
auto swap_with = it->index_in_vector;
if (swap_with < m_entry_vector.size() - 1) {
m_entry_vector.back()->index_in_vector = swap_with;
m_entry_vector[swap_with] = m_entry_vector.back();
}
m_entry_set.erase(it);
m_entry_vector.pop_back();
return 1;
}
template <typename RandomGenerator>
const T & random_element(RandomGenerator & r)
{
std::uniform_int_distribution<> dis(0, m_entry_vector.size() - 1);
return m_entry_vector[dis(r)]->data;
}
private:
std::unordered_set<std::unique_ptr<Entry>, PtrEntryHash, PtrEntryEqual>
m_entry_set;
std::vector<Entry*> m_entry_vector;
};
Notes:
- This implementation is just a skeleton, where additional operations might be added.
- If this is to be a library class, then it is best to make it a proper container, with an iterator type, which hides the implementation details, and with
begin() and end() calls, and with a better return type for insert().