Offsetting a polyline in one direction

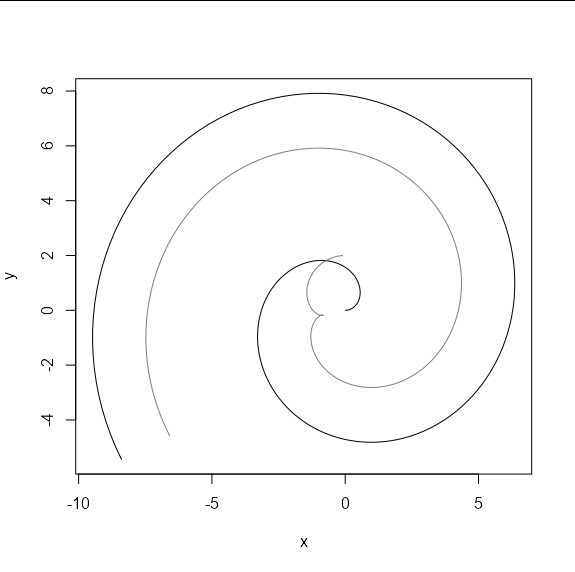
I'm looking for a way to offset an arbitrary curve defined through xy-coordinates in one direction (in R). I can use the {polyclip} package to offset the curve in two directions.

library(polyclip)
#> polyclip 1.10-0 built from Clipper C++ version 6.4.0

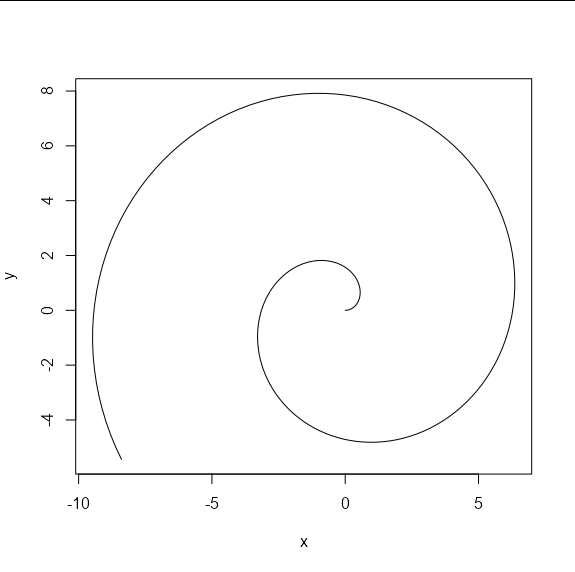
# Make a curve
t <- seq(10, 0, by = -0.05)
curve <- data.frame(
  x = t * cos(t), y = t * sin(t)
)
plot(curve, type = 'l')

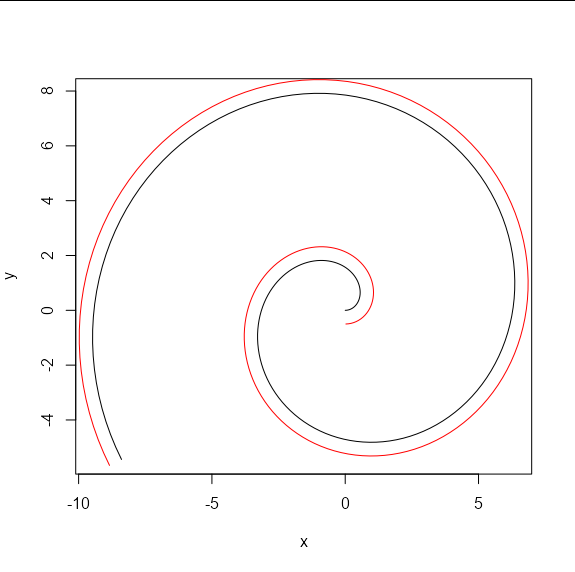
# Find offset
offset <- polylineoffset(curve, delta = 0.5, 
                         jointype = "round", endtype = "openbutt")[[1]]
offset <- as.data.frame(offset) # xy coordinates

lines(offset, col = "red")

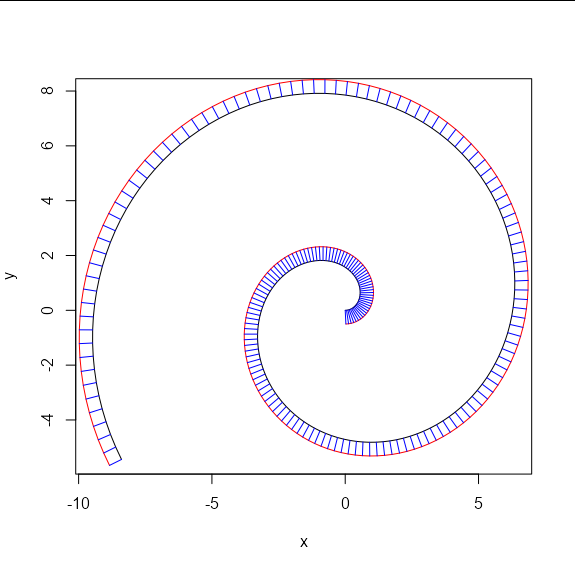
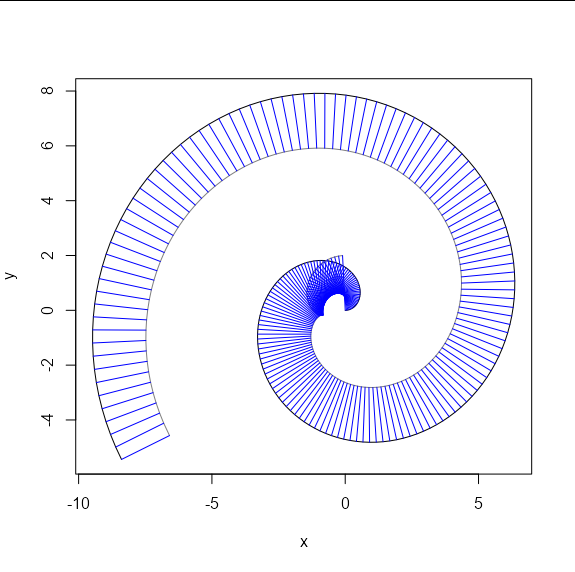
Because the points on the curve are more closely spaced than the offset's delta parameter, I can heuristically split the offset by finding out where the distance between a point and the next is the largest.

distance <- c(0, sqrt(diff(offset$x)^2 + sqrt(diff(offset$y)^2)))
max_dist <- which.max(distance)

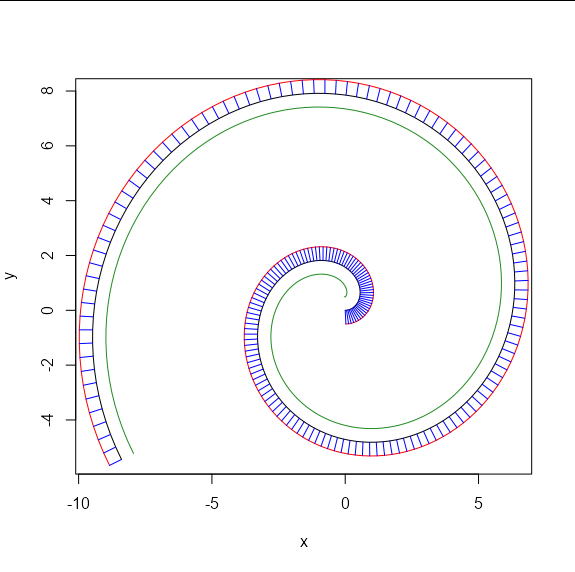
plot(curve, type = 'l')
lines(offset[1:(max_dist - 1), ], col = 3)
lines(offset[max_dist:nrow(offset), ], col = 4)

^{Created on 2021-11-11 by the reprex package (v2.0.1)}

However, I would like to be able to split the offset, or offset in just one direction, even if the points on the curve are further apart than the offset distance. Is there a way to do this in R? I'm not married to the {polyclip} package, a solution using another package is fine too.

No need for extra packages Teunbrand - this can done with a small trig function:

offset <- function(x, y, d) {
 angle <- atan2(diff(y), diff(x)) + pi/2
 angle <- c(angle[1], angle)
 data.frame(x = d * cos(angle) + x, y = d * sin(angle) + y)
}

So, if we recreate your example we have:

t <- seq(10, 0, by = -0.05)

curve <- data.frame(
  x = t * cos(t), y = t * sin(t)
)

plot(curve, type = 'l')

And we can add an offset with:

curve2 <- offset(curve$x, curve$y, 0.5)

lines(curve2, col = "red")

The way this function works is by getting the angle of the slope at each point of the line using atan2([delta y], [delta x]), then adding 90 degrees to find the angle of a line running perpendicular to the curve at that point. Finally, it finds the point that is distance d along this line from the original x, y co-ordinate, which is (x + d * cos(angle), y + d * sin(angle))

This is maybe best shown graphically. The blue lines here are the offsets calculated by the function offset:

segments(curve$x, curve$y, curve2$x, curve2$y, col = "blue")

We can offset in the opposite direction by simply passing a negative value of d:

lines(offset(curve$x, curve$y, -0.5), col = "forestgreen")

We need to be aware of the limitations of defining what we mean by an offset, particularly when the offset is large compared to any concave sections of the plot. For example, if we look at an offset of -2, we seem to have an artifact at the center of our spiral:

plot(curve, type = 'l')
curve3 <- offset(curve$x, curve$y, -2)
lines(curve3, col = "gray50")

We can see why this happens if we draw the offset segments again:

segments(curve$x, curve$y, curve3$x, curve3$y, col = "blue")

Essentially, if you have a tight concave curve and a fairly large offset, then the offset lines will cross. This produces something that doesn't quite match with what we would expect to see with an "offset path", but it is difficult to see how this could be fixed without carefully defining what we mean by an offset path, and how we would want it to appear in situations like the one above. My guess is that the most satisfactory solution would be to shrink d at the points where it would otherwise exceed the radius of the curve at that point, but I won't implement that here as this is only one option, and I'm sure there are better ones out there.

Anyway, one of the benefits of doing it this way is that the number of points in the result is the same as the number that went in. This makes it easy to have the offsets put into your initial data frame. Handy for building new geoms!

^{Created on 2021-11-12 by the reprex package (v2.0.0)}

Recommended topics

Hot tags