Difference between symbolic differentiation and automatic differentiation?

Question

I just cannot seem to understand the difference. For me it looks like both just go through an expression and apply the chain rule.. What am I missing?

Nardi

Are you lookin at basic equations with one variable or mutli-variables? Also I would give an answer, but my knowledge of automatic-differentiation is not as good as symbolic math. If I have time I might look into this more and post an answer. – Mccaslin

Answer 1

There are 3 popular methods to calculate the derivative:

1. Numerical differentiation
2. Symbolic differentiation
3. Automatic differentiation

Numerical differentiation relies on the definition of the derivative: 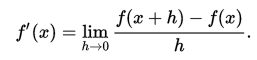, where you put a very small h and evaluate function in two places. This is the most basic formula and on practice people use other formulas which give smaller estimation error. This way of calculating a derivative is suitable mostly if you do not know your function and can only sample it. Also it requires a lot of computation for a high-dim function.

Symbolic differentiation manipulates mathematical expressions. If you ever used matlab or mathematica, then you saw something like this

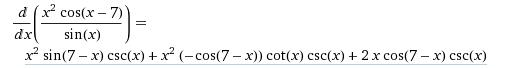
Here for every math expression they know the derivative and use various rules (product rule, chain rule) to calculate the resulting derivative. Then they simplify the end expression to obtain the resulting expression.

Automatic differentiation manipulates blocks of computer programs. A differentiator has the rules for taking the derivative of each element of a program (when you define any op in core TF, you need to register a gradient for this op). It also uses chain rule to break complex expressions into simpler ones. Here is a good example how it works in real TF programs with some explanation.

---

You might think that Automatic differentiation is the same as Symbolic differentiation (in one place they operate on math expression, in another on computer programs). And yes, they are sometimes very similar. But for control flow statements (`if, while, loops) the results can be very different:

symbolic differentiation leads to inefficient code (unless carefully done) and faces the difficulty of converting a computer program into a single expression

Quoin

Would you please explain_'for control flow statements (`if, while, loops) the results can be very different'? – Consistency

"register a gradient" link is broken – Ss

Answer 2

It is a common claim, that automatic differentiation and symbolic differentiation are different. However, this is not true. Forward mode automatic differentiation and symbolic differentiation are in fact equivalent. Please see this paper.

In short, they both apply the chain rule from the input variables to the output variables of an expression graph. It is often said, that symbolic differentiation operates on mathematical expressions and automatic differentiation on computer programs. In the end, they are actually both represented as expression graphs.

On the other hand, automatic differentiation also provides more modes. For instance, when applying the chain rule from output variables to input variables then this is called reverse mode automatic differentiation.

Capillarity

This paper is extremely misleading, and if the conclusions are right, they're only right in a very artificial sense. I agree that forward mode AD and symbolic differentiation are "algorithmically equivalent", but in no way are they in fact equivalent. This comment is confusing to someone trying to understand the difference between AD and symbolic differentiation. – Pilkington

Many authors have claimed that AD and SD are fundamentally different but have failed to show any difference. Not only are they "algorithmically equivalent" they are also numerically and computationally equivalent. In fact, many of the authors who first described AD have since acknowledged this equivalence, including Griewank (2019) "There is still confusion about the difference between "automatic", "symbolic" and "analytic" differentiation. In my book they are all the same," and Elliott (2018), “AD is SD performed by a compiler.” – Tana

You wrote the paper (which really is a preprint). As an outsider, it seems like you may not be best positioned to recommend it as an objective source. – Endodermis

@NickMcGreivy How so? – Ronaldronalda

@Ronaldronalda good question. The difference is that algorithmic differentiation manipulates mathematical expressions, while forward mode AD manipulates numbers. Each uses as a graph of expressions, but the key difference (which the question is asking for) is numbers versus expressions. – Pilkington

@NickMcGreivy The statement/differentiation that symbolic differentiation manipulates mathematical expressions and AD manipulates numbers is not correct. This is often a misconception. AD sometimes manipulates numbers but it also manipulates mathematical expressions, usually given as code. This is known as source code transformation in AD. See, e.g., Wikipedia AD. – Capillarity

@Capillarity I think symbolic diff normally gives you an entire equation expression, while autodiff only evaluates the basic differentiation rules without requiring a final equation. For example, (x1 * x2 * sin(x3) - exp(x1 * x2)) / x3, the symbolic diff will return the grad expression w.r.t x1, x2 and x3 separately. But for autodiff, you only need to provide, say, what "+" or "-" rule is, what "sin" rule is, what "/" rule is, what "exp" rule is, and what "*" rule is. And you never need to refer to the function itself it get the symbolic form. Once you define the rule, it works on any functions. – Supererogate

Answer 3

"For me it looks like both just go through an expression and apply the chain rule. What am I missing?"

What you're missing is that AD works with numerical values, while symbolic differentiation works with symbols which represent those values. Let's look at simple example to flesh this out.

Suppose I want to compute the derivative of the expression y = x^2.

If I were doing symbolic differentiation, I would start with the symbol x, and I would square it to get y = x^2, and then I would use the chain rule to know that the dervivate dy/dx = 2x. Now, if I want the derivative for x=5, I can plug that into my expression, and get the derivative. But since I have the expression for the derivative, I can plug in any value of x and compute the derivative without having to repeat the chain rule computations.

If I were doing automatic differentiation, I would start with the value x = 5, and then compute y = 5^2 = 25, and compute the derivative as dy/dx = 2*5 = 10. I would have computed the value and the derivative. However, I know nothing about the value of the derivative at x=4. I would have to repeat the process with x=4 to get the derivative at x=4.

Pilkington

Unfortunately, this answer is not correct. It does not describe the difference between symbolic and algorithmic/automatic differentiation. It describes the difference between static (define-and-run) and dynamic (define-by-run) AD. Both are two AD implementations. The first ist often executed by source code transformation, the latter using operator overloading. See, e.g.,wikipedia or this paper (page 18). – Capillarity

The opening sentence of this answer is correct. AD works with numerical values based on a dual number. However, the classification is misleading. As @Capillarity explains, It's the difference between the dynamic and static AD. For example, the Tensorflow gradient tape implements dynamic AD (define-by-run). That's why to compute the gradient of a variable the tape required to watch the variable. AD is not equivalent to SD but the way it finding derivative is similarly by disassembling an equation. In AD the equation dissembled into a graph while in SD in the form of symbol blocks. – Varix

@Willysatrionugroho Static AD builds a graph of primitive functions, then computes the value and derivative by passing numbers through that graph. Symbolic differentiation creates chained expressions to get a symbolic representation of the derivative, but never passes numbers around. The 1st paragraph describes symbolic diff because explicit expressions are created. The 2nd paragraph describes AD because numbers are passed through primitives but the full expression is never computed. It doesn't matter whether the primitives are chained via a static graph or dynamically from the interpreter. – Pilkington

@NickMcGreivy I admit AD also implements SD underneath. But let's say we need some additional variables while we solve the equation. We need predefined symbols before we able to solve the equation. In SD we have to prepare the symbols because the correct chain expression is mandatory. Meanwhile, in AD we can enjoy the autogenerated symbols. I also don't think AD is superior to SD. Because the real reason of more ML frameworks using AD is due to it's easier to understand by the developers. For technical things, I think it's interesting to test SD & AD time and memory complexity in some cases. – Varix