Bug in the C++ standard library in std::poisson_distribution?

Question

I think I have encountered an incorrect behaviour of std::poisson_distribution from C++ standard library.

Questions:

1. Could you confirm it is indeed a bug and not my error?
2. What exactly is wrong in the standard library code of poisson_distribution function, assuming that it is indeed a bug?

Details:

The following C++ code (file poisson_test.cc) is used to generate Poisson-distributed numbers:

#include <array>
#include <cmath>
#include <iostream>
#include <random>

int main() {
  // The problem turned out to be independent on the engine
  std::mt19937_64 engine;

  // Set fixed seed for easy reproducibility
  // The problem turned out to be independent on seed
  engine.seed(1);
  std::poisson_distribution<int> distribution(157.17);

  for (int i = 0; i < 1E8; i++) {
    const int number = distribution(engine);
    std::cout << number << std::endl;
  }
}

I compile this code as follows:

clang++ -o poisson_test -std=c++11 poisson_test.cc
./poisson_test > mypoisson.txt

The following python script was used to analyze the sequence of random numbers from file mypoisson.txt:

import numpy as np
import matplotlib.pyplot as plt

def expectation(x, m):
    " Poisson pdf " 
    # Use Ramanujan formula to get ln n!
    lnx = x * np.log(x) - x + 1./6. * np.log(x * (1 + 4*x*(1+2*x))) + 1./2. * np.log(np.pi)
    return np.exp(x*np.log(m) - m - lnx)

data = np.loadtxt('mypoisson.txt', dtype = 'int')

unique, counts = np.unique(data, return_counts = True)
hist = counts.astype(float) / counts.sum()
stat_err = np.sqrt(counts) / counts.sum()
plt.errorbar(unique, hist, yerr = stat_err, fmt = '.', \
             label = 'Poisson generated \n by std::poisson_distribution')
plt.plot(unique, expectation(unique, expected_mean), \
         label = 'expected probability \n density function')
plt.legend()
plt.show()

# Determine bins with statistical significance of deviation larger than 3 sigma
deviation_in_sigma = (hist - expectation(unique, expected_mean)) / stat_err
d = dict((k, v) for k, v in zip(unique, deviation_in_sigma) if np.abs(v) > 3.0)
print d

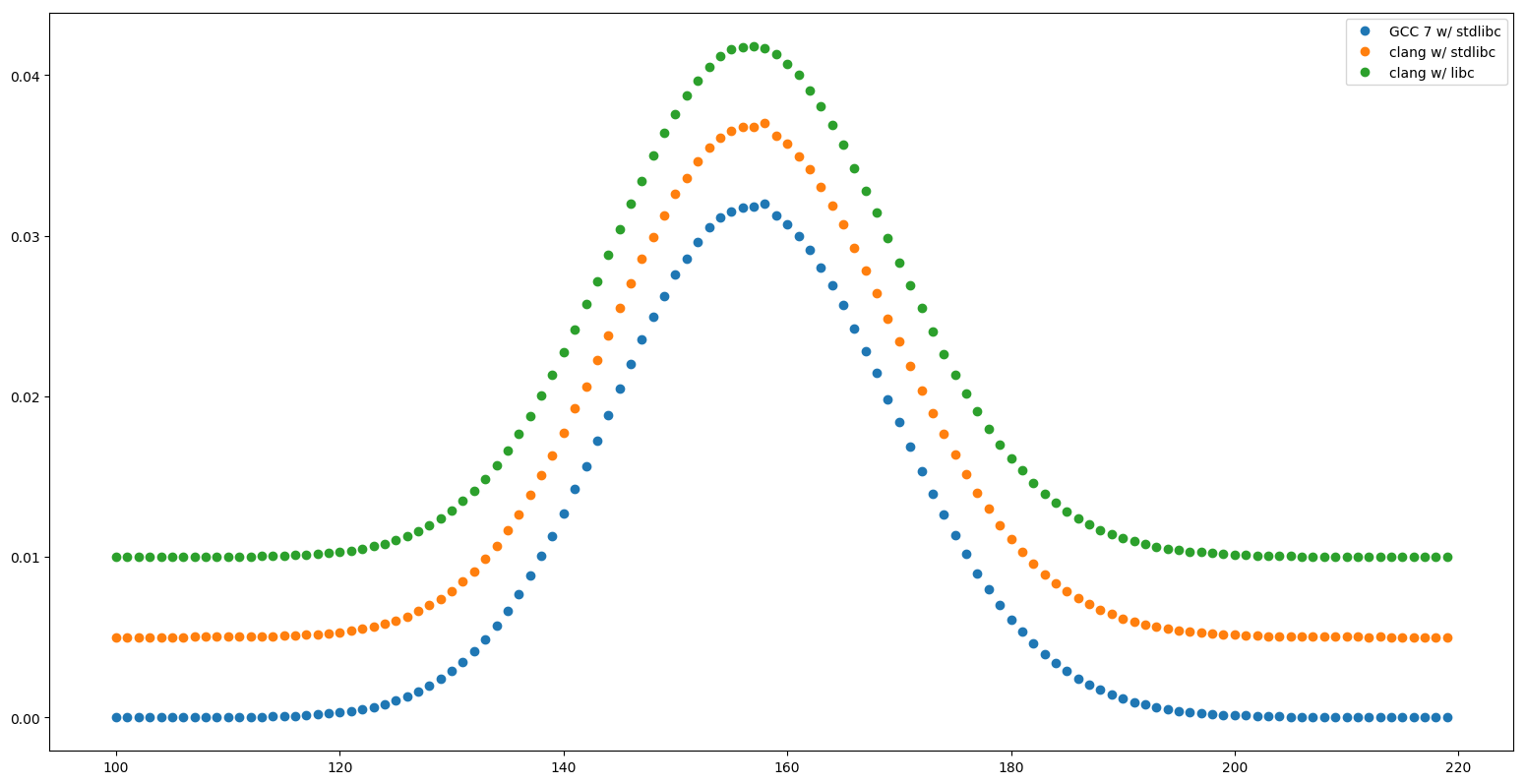
The script produces the following plot:

You can see the problem by bare eye. The deviation at n = 158 is statistically significant, it is in fact a 22σ deviation!

Close-up of the previous plot.

Recreate

Which standard library is it? AFAIK, Clang tends to use libstdc++ on Linux and libc++ on Mac. – Kerk

@Kerk I am on Ubuntu, I have checked that it is libstdc++. Printing out ____GLIBCXX____ gives 20160609. Concerning clang version, "clang -v" gives "clang version 3.8.0-2ubuntu4 (tags/RELEASE_380/final)" Can you reproduce the bug on Mac? – Recreate

I don't have a Mac handy, I was simply verifying which implementation was actually being used because the two are wildly different. – Kerk

I've compiled and run using Visual C++ 2017 (32 bit build) and I don't get the outlier. (Value for 158 is around 0.03166, slightly lower than the value for 157 of 0.03182) – Soda

Please report that bug and give its URL in your question – Papeete

Just a comment on the maths, the Poisson distribution is not continuous but discrete, and thus does not have a probability density function. You can calculate the probability mass function, though. I realize that your line plot helps to guide the eye, but the Poisson distribution does have non-integer variates, so plotting a continuous line is a bit misleading. – Amphichroic

Looking at the source: // NB: This case not in the book, nor in the Errata, but should be ok... - I don't know a thing about the problem at hand (besides some very basic uni stuff about accept/reject algorithm), but it's the kind of statement that makes me nervous... :o) – Dinnie

@MatteoItalia Haha, I found the same piece of code, and was slightly worried as well. – Amphichroic

@ChristophTerasa You are certainly right about probability density/mass function. I was taught statistics in Russian, so no wonder I have misused the term here. However note, that there is also a continuous counterpart of Poisson distribution (see e.g. arxiv.org/abs/1303.5990 and its reference to the book of Knuth), which can be used and is sometimes used to generate the discrete Poisson distribution. – Recreate

Answer 1

My system is set up as follows (Debian testing):

libstdc++-7-dev:
  Installed: 7.2.0-16

libc++-dev:
  Installed: 3.5-2

clang:
  Installed: 1:3.8-37

g++:
  Installed: 4:7.2.0-1d1

I can confirm the bug when using libstdc++:

g++ -o pois_gcc -std=c++11 pois.cpp
clang++ -o pois_clang -std=c++11 -stdlib=libstdc++ pois.cpp
clang++ -o pois_clang_libc -std=c++11 -stdlib=libc++ pois.cpp

Result:

Amphichroic

Did you report that bug? You probably should! Then give its URL in your question! – Papeete

Credit does not go to me. I'd wait for @DmytroOliinychenko to report this, if he wants. Though if he decides not to I can do this as well. – Amphichroic

Reported to GCC bugtracker. – Amphichroic

@ChristophTerasa please link to the bug report – Forbis

GCC bugtracker link: gcc.gnu.org/bugzilla/show_bug.cgi?id=83237 – Amphichroic

@ChristophTerasa Thank you! This answer is very helpful, since now I know I can simply compile with "-stdlib=libc++" to get the correct distribution. I am tempted to accept this as the final correct answer, but as a scientist I wonder what's wrong with the libstdc++ implementation. That comment in the source code (// NB: This case not in the book, nor in the Errata, but should be ok...) is certainly suspicious, but I wasn't able to prove it is responsible for the bug. – Recreate