3D Least Squares Plane

Question

What's the algorithm for computing a least squares plane in (x, y, z) space, given a set of 3D data points? In other words, if I had a bunch of points like (1, 2, 3), (4, 5, 6), (7, 8, 9), etc., how would one go about calculating the best fit plane f(x, y) = ax + by + c? What's the algorithm for getting a, b, and c out of a set of 3D points?

Sensuous

You should define what exactly you mean by "least squares". See e.g. en.wikipedia.org/wiki/Least_squares for various ways of defining it. – Dufrene

This is a comment. If someone would be so kind as to move it into the comments for Stephen Canon's answer, that would be great. This, I hope, clarifies what the heck he meant by "The three components of the solution vector are the coefficients to the least-square fit plane {a,b,c}." First, it is elementary matrix algebra that given Ax = b where A is a matrix, and b and x are vectors that the solution only exists if A has a non-zero determinant. Which means you need more than 3 points and that at least one point should not be on the plane (not exact). The second clarification, and the reaso – Unplug

Answer 1

If you have n data points (x[i], y[i], z[i]), compute the 3x3 symmetric matrix A whose entries are:

sum_i x[i]*x[i],    sum_i x[i]*y[i],    sum_i x[i]
sum_i x[i]*y[i],    sum_i y[i]*y[i],    sum_i y[i]
sum_i x[i],         sum_i y[i],         n

Also compute the 3 element vector b:

{sum_i x[i]*z[i],   sum_i y[i]*z[i],    sum_i z[i]}

Then solve Ax = b for the given A and b. The three components of the solution vector are the coefficients to the least-square fit plane {a,b,c}.

Note that this is the "ordinary least squares" fit, which is appropriate only when z is expected to be a linear function of x and y. If you are looking more generally for a "best fit plane" in 3-space, you may want to learn about "geometric" least squares.

Note also that this will fail if your points are in a line, as your example points are.

Ovida

Only three parameters? Would this be a plane that necessarily includes the origin? Hmm...good enough if we first remove the center of mass. Nice. – Issy

Three parameters suffice to describe every plane that can be written as a function of x an y, which is what I believe the OP is asking for. If you have such a plane in general form (ax + by + cz + d = 0), you can just solve for z and eliminate a parameter: z = (-a/c)x + (-b/c)y + (-d/c). – Ovida

I believe there is a "Faster" method using Principle Component Analysis, and its the generally accepted method to fit a plane. – Benefice

There are three common methods. The SVD-based method to which you refer is preferred for some problems, but is much harder to explain (and to understand) than the fairly elementary "Normal Equations" that I used. The SVD-based method is actually slower than solving the normal equations, but is preferred because it is more numerically stable. – Ovida

en.wikipedia.org/wiki/… has more details if you want to learn about all the different LLS algorithms. – Ovida

ahh yea, thats why I didn't post an answer because I've never used PCA before I just assumed its faster because I know its the commonly accepted tool for the job. From what I understand PCA involved finding the eigenbasis and thats a very common problem that problably has some efficient algorithms. – Benefice

@StephenCanon: nice writeup. Question on your comment about SVD: Is the SVD method more numerically stable only because it is doing the matrix solution more stably? Since this is a 3x3 problem, one could obtain a closed form solution symbolically to the normal equations method. In this case it would seem that the only numerical issues then would be the size of the determinant of A which scales the answer. Assuming non-zero (non-small) determinant, would the SVD method still be more stable than the symbolical closed form normal equations method? Interested in your view. Thanks. – Spinelli

@AKE: No, when you use QR or SVD, you don’t use the normal equations (meaning you don’t form the 3x3 matrix I described, but instead operate directly on the nx3 matrix of measurements). This results in better stability (a) because orthogonal factorizations have good stability properties and more importantly (b) because the condition number of XtX is the square of the condition number of X. – Ovida

@StephenCanon: So if I understand you right, whether or not the matrix inversion in the normal equations method is symbolic is a red herring. The difference in stability comes from the approach of the QR or SVD methods vs. the approach of the normal equatios method (inverting a matrix). Is that what you mean? – Spinelli

I have implemented this code. What can be the reason for me to get z=0 plane all the time? I get (a,b,c) and create the plane with the equation ax + by + cz. Should I do more? – Ciapha

Where could I find an explanation of this method, especially the way the matrices were made and why the solution vector is equal to plane's coefficients? I saw the Wikipedia article, but it goes over very general equations which don't really help me. – Condemnation

I think you can find some explanation in this article ilikebigbits.com/blog/2015/3/2/plane-from-points – Gaelic

@Condemnation You can find an explanation also in "Least Squares Fitting of Data" by David Eberly at geometrictools.com/Documentation/LeastSquaresFitting.pdf – Aforesaid

Please provide the actual plane equation that you solve by finding X, – Alexio

Answer 2

The equation for a plane is: ax + by + c = z. So set up matrices like this with all your data:

    x_0   y_0   1  
A = x_1   y_1   1  
          ... 
    x_n   y_n   1  

And

    a  
x = b  
    c

And

    z_0   
B = z_1   
    ...   
    z_n

In other words: Ax = B. Now solve for x which are your coefficients. But since (I assume) you have more than 3 points, the system is over-determined so you need to use the left pseudo inverse. So the answer is:

a 
b = (A^T A)^-1 A^T B
c

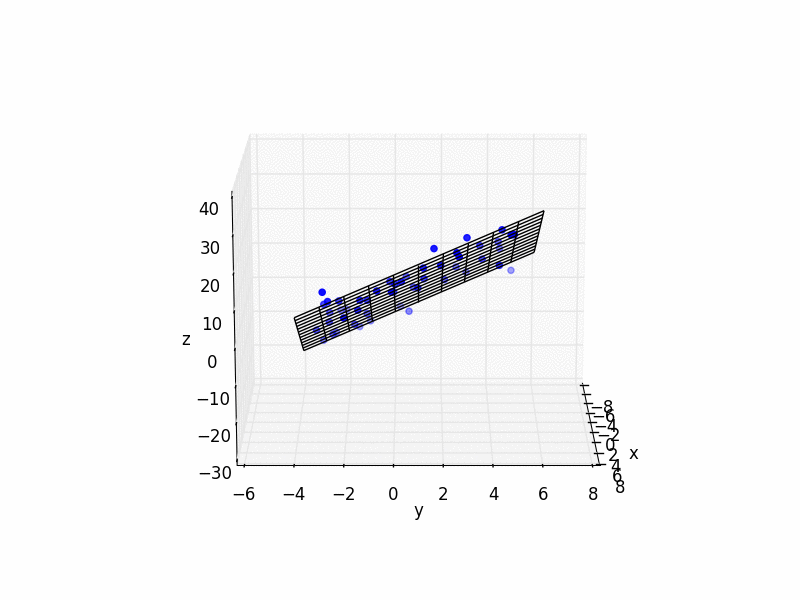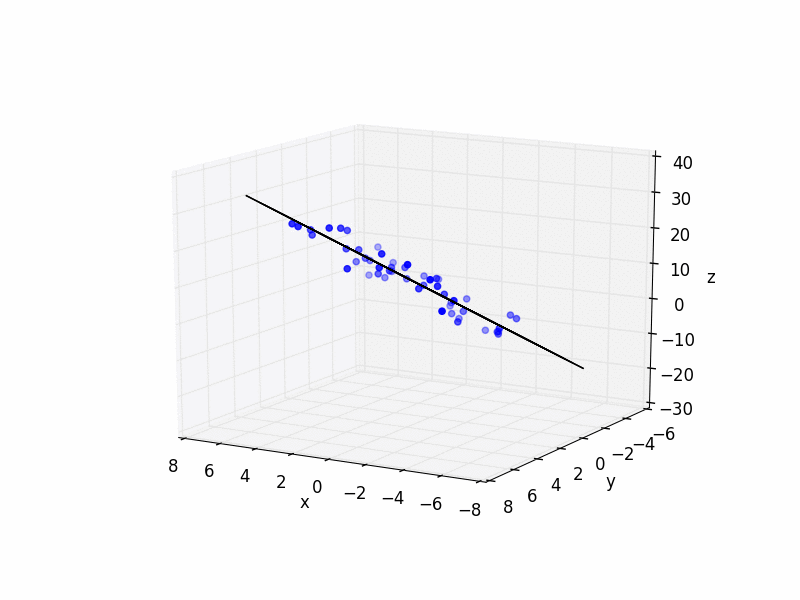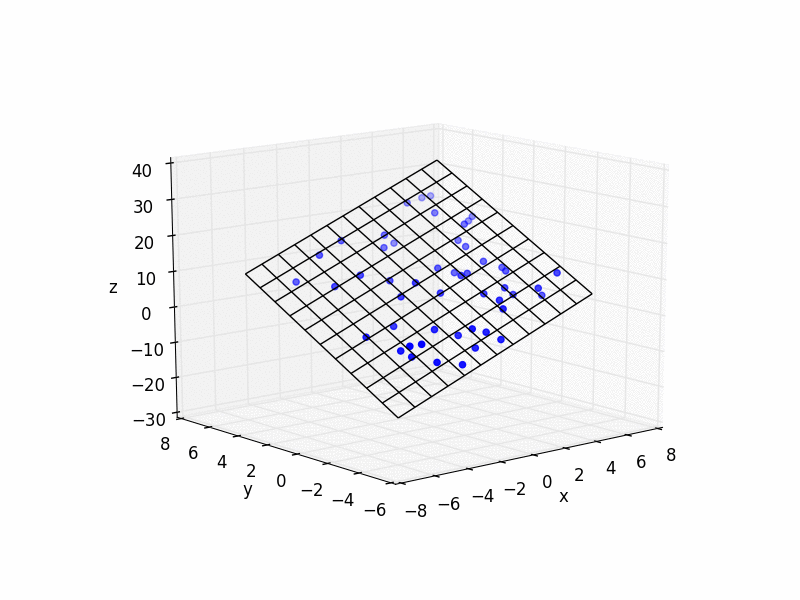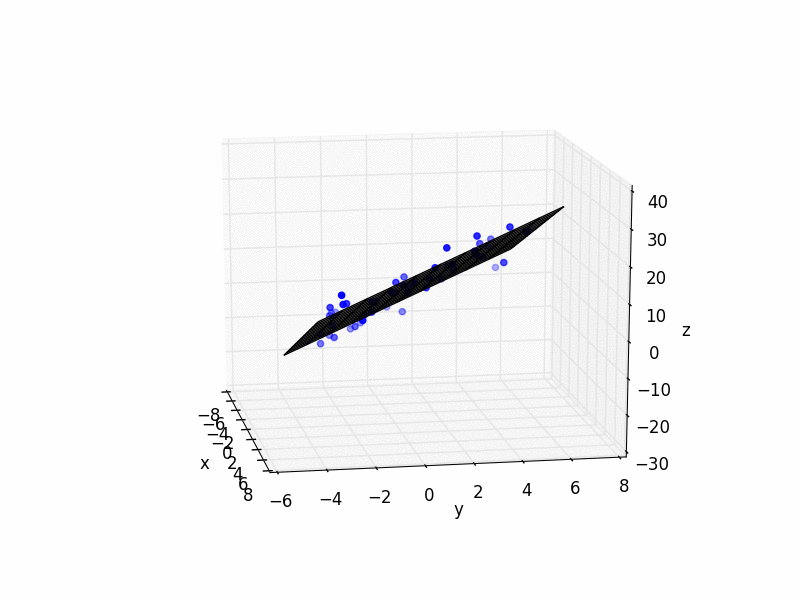
And here is some simple Python code with an example:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

N_POINTS = 10
TARGET_X_SLOPE = 2
TARGET_y_SLOPE = 3
TARGET_OFFSET  = 5
EXTENTS = 5
NOISE = 5

# create random data
xs = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
ys = [np.random.uniform(2*EXTENTS)-EXTENTS for i in range(N_POINTS)]
zs = []
for i in range(N_POINTS):
    zs.append(xs[i]*TARGET_X_SLOPE + \
              ys[i]*TARGET_y_SLOPE + \
              TARGET_OFFSET + np.random.normal(scale=NOISE))

# plot raw data
plt.figure()
ax = plt.subplot(111, projection='3d')
ax.scatter(xs, ys, zs, color='b')

# do fit
tmp_A = []
tmp_b = []
for i in range(len(xs)):
    tmp_A.append([xs[i], ys[i], 1])
    tmp_b.append(zs[i])
b = np.matrix(tmp_b).T
A = np.matrix(tmp_A)
fit = (A.T * A).I * A.T * b
errors = b - A * fit
residual = np.linalg.norm(errors)

print("solution:")
print("%f x + %f y + %f = z" % (fit[0], fit[1], fit[2]))
print("errors:")
print(errors)
print("residual:")
print(residual)

# plot plane
xlim = ax.get_xlim()
ylim = ax.get_ylim()
X,Y = np.meshgrid(np.arange(xlim[0], xlim[1]),
                  np.arange(ylim[0], ylim[1]))
Z = np.zeros(X.shape)
for r in range(X.shape[0]):
    for c in range(X.shape[1]):
        Z[r,c] = fit[0] * X[r,c] + fit[1] * Y[r,c] + fit[2]
ax.plot_wireframe(X,Y,Z, color='k')

ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()

Trochal

Gives "Singular matrix" error if: xs = [] ys = [] zs = [] for i in range(N_POINTS): xs.append(i * i) ys.append(0) zs.append(1) – Varela

@Alexey, your input points are in a straight line. So there are infinite planes that fit the data equally well. This is a degenerate case so the least squares solution won't work. Actually, I'm not sure any general purpose solution will work with it. If you have a specific question, please open a new question, possibly referencing this one. – Trochal

Hi Ben, thanks for this. Can u also provide a link/text explaining how you went from ax + by + dz + c = 0 to ax + by + c = z ? Aren't you assuming that the z-component of the plane normal is always one ? – Submarine

In linear algebra, same as regular algebra, you can subtract z from both sides of the equation to make one side zero. This site doesn't support mathjax. Perhaps it is more clear here. – Trochal

Answer 3

unless someone tells me how to type equations here, let me just write down the final computations you have to do:

first, given points r_i \n \R, i=1..N, calculate the center of mass of all points:

r_G = \frac{\sum_{i=1}^N r_i}{N}

then, calculate the normal vector n, that together with the base vector r_G defines the plane by calculating the 3x3 matrix A as

A = \sum_{i=1}^N (r_i - r_G)(r_i - r_G)^T

with this matrix, the normal vector n is now given by the eigenvector of A corresponding to the minimal eigenvalue of A.

To find out about the eigenvector/eigenvalue pairs, use any linear algebra library of your choice.

This solution is based on the Rayleight-Ritz Theorem for the Hermitian matrix A.

Ancheta

can you tell me where you got that from? I can't quite see the connection to the Rayleight-Ritz Theorem ?? – Ventricose

@Ancheta No LaTeX here. See meta.stackexchange.com/questions/30559/latex-on-stack-overflow – Wanton

Answer 4

See 'Least Squares Fitting of Data' by David Eberly for how I came up with this one to minimize the geometric fit (orthogonal distance from points to the plane).

bool Geom_utils::Fit_plane_direct(const arma::mat& pts_in, Plane& plane_out)
{
    bool success(false);
    int K(pts_in.n_cols);
    if(pts_in.n_rows == 3 && K > 2)  // check for bad sizing and indeterminate case
    {
        plane_out._p_3 = (1.0/static_cast<double>(K))*arma::sum(pts_in,1);
        arma::mat A(pts_in);
        A.each_col() -= plane_out._p_3; //[x1-p, x2-p, ..., xk-p]
        arma::mat33 M(A*A.t());
        arma::vec3 D;
        arma::mat33 V;
        if(arma::eig_sym(D,V,M))
        {
            // diagonalization succeeded
            plane_out._n_3 = V.col(0); // in ascending order by default
            if(plane_out._n_3(2) < 0)
            {
                plane_out._n_3 = -plane_out._n_3; // upward pointing
            }
            success = true;
        }
    }
    return success;
}

Timed at 37 micro seconds fitting a plane to 1000 points (Windows 7, i7, 32bit program)

Robertson

Answer 5

This reduces to the Total Least Squares problem, that can be solved using SVD decomposition.

C++ code using OpenCV:

float fitPlaneToSetOfPoints(const std::vector<cv::Point3f> &pts, cv::Point3f &p0, cv::Vec3f &nml) {
    const int SCALAR_TYPE = CV_32F;
    typedef float ScalarType;

    // Calculate centroid
    p0 = cv::Point3f(0,0,0);
    for (int i = 0; i < pts.size(); ++i)
        p0 = p0 + conv<cv::Vec3f>(pts[i]);
    p0 *= 1.0/pts.size();

    // Compose data matrix subtracting the centroid from each point
    cv::Mat Q(pts.size(), 3, SCALAR_TYPE);
    for (int i = 0; i < pts.size(); ++i) {
        Q.at<ScalarType>(i,0) = pts[i].x - p0.x;
        Q.at<ScalarType>(i,1) = pts[i].y - p0.y;
        Q.at<ScalarType>(i,2) = pts[i].z - p0.z;
    }

    // Compute SVD decomposition and the Total Least Squares solution, which is the eigenvector corresponding to the least eigenvalue
    cv::SVD svd(Q, cv::SVD::MODIFY_A|cv::SVD::FULL_UV);
    nml = svd.vt.row(2);

    // Calculate the actual RMS error
    float err = 0;
    for (int i = 0; i < pts.size(); ++i)
        err += powf(nml.dot(pts[i] - p0), 2);
    err = sqrtf(err / pts.size());

    return err;
}

Maxim

what is conv function? It's not OpenCV one, right? – Doroteya

Right, I don't think it was opencv. It's just a conversion from Point3f to Vec3f, same as subtracting cv::Point3f(0,0,0). – Maxim

Answer 6

As with any least-squares approach, you proceed like this:

Before you start coding

1. Write down an equation for a plane in some parameterization, say 0 = ax + by + z + d in thee parameters (a, b, d).

2. Find an expression D(\vec{v};a, b, d) for the distance from an arbitrary point \vec{v}.

3. Write down the sum S = \sigma_i=0,n D^2(\vec{x}_i), and simplify until it is expressed in terms of simple sums of the components of v like \sigma v_x, \sigma v_y^2, \sigma v_x*v_z ...

4. Write down the per parameter minimization expressions dS/dx_0 = 0, dS/dy_0 = 0 ... which gives you a set of three equations in three parameters and the sums from the previous step.

5. Solve this set of equations for the parameters.

(or for simple cases, just look up the form). Using a symbolic algebra package (like Mathematica) could make you life much easier.

The coding

• Write code to form the needed sums and find the parameters from the last set above.

Alternatives

Note that if you actually had only three points, you'd be better just finding the plane that goes through them.

Also, if the analytic solution in unfeasible (not the case for a plane, but possible in general) you can do steps 1 and 2, and use a Monte Carlo minimizer on the sum in step 3.

Issy

please consider changing the unparsed LaTex code to a more readable form. – Submarine

Answer 7

CGAL::linear_least_squares_fitting_3

Function linear_least_squares_fitting_3 computes the best fitting 3D line or plane (in the least squares sense) of a set of 3D objects such as points, segments, triangles, spheres, balls, cuboids or tetrahedra.

http://www.cgal.org/Manual/latest/doc_html/cgal_manual/Principal_component_analysis_ref/Function_linear_least_squares_fitting_3.html

Aforesaid

Answer 8

It sounds like all you want to do is linear regression with 2 regressors. The wikipedia page on the subject should tell you all you need to know and then some.

Susurrant

Answer 9

All you'll have to do is to solve the system of equations.

If those are your points: (1, 2, 3), (4, 5, 6), (7, 8, 9)

That gives you the equations:

3=a*1 + b*2 + c
6=a*4 + b*5 + c
9=a*7 + b*8 + c

So your question actually should be: How do I solve a system of equations?

Therefore I recommend reading this SO question.

If I've misunderstood your question let us know.

EDIT:

Ignore my answer as you probably meant something else.

Juju

The OPs example is bad because he gives three points but he wants to solve the general case given n points and hence a overconstraint system. If not all points are in a plane, he wants to find the best fit, that is the plane minimizing the distance of all points from the plane in a least square sence. – Juno

Answer 10

We first present a linear least-squares plane fitting method that minimizes the residuals between the estimated normal vector and provided points.

Recall that the equation for a plane passing through origin is Ax + By + Cz = 0, where (x, y, z) can be any point on the plane and (A, B, C) is the normal vector perpendicular to this plane.

The equation for a general plane (that may or may not pass through origin) is Ax + By + Cz + D = 0, where the additional coefficient D represents how far the plane is away from the origin, along the direction of the normal vector of the plane. [Note that in this equation (A, B, C) forms a unit normal vector.]

Now, we can apply a trick here and fit the plane using only provided point coordinates. Divide both sides by D and rearrange this term to the right-hand side. This leads to A/D x + B/D y + C/D z = -1. [Note that in this equation (A/D, B/D, C/D) forms a normal vector with length 1/D.]

We can set up a system of linear equations accordingly, and then solve it by an Eigen solver in C++ as follows.

// Example for 5 points
Eigen::Matrix<double, 5, 3> matA; // row: 5 points; column: xyz coordinates
Eigen::Matrix<double, 5, 1> matB = -1 * Eigen::Matrix<double, 5, 1>::Ones();

// Find the plane normal
Eigen::Vector3d normal = matA.colPivHouseholderQr().solve(matB);

// Check if the fitting is healthy
double D = 1 / normal.norm();
normal.normalize(); // normal is a unit vector from now on
bool planeValid = true;
for (int i = 0; i < 5; ++i) { // compare Ax + By + Cz + D with 0.2 (ideally Ax + By + Cz + D = 0)
  if ( fabs( normal(0)*matA(i, 0) + normal(1)*matA(i, 1) + normal(2)*matA(i, 2) + D) > 0.2) {
    planeValid = false; // 0.2 is an experimental threshold; can be tuned
    break;
  }
}

We then discuss its equivalence to the typical SVD-based method and their comparison.

The aforementioned linear least-squares (LLS) method fits the general plane equation Ax + By + Cz + D = 0, whereas the SVD-based method replaces D with D = - (Ax0 + By0 + Cz0) and fits the plane equation A(x-x0) + B(y-y0) + C(z-z0) = 0, where (x0, y0, z0) is the mean of all points that serves as the origin of the new local coordinate frame.

Comparison between two methods:

• The LLS fitting method is much faster than the SVD-based method, and is suitable for use when points are known to be roughly in a plane shape.
• The SVD-based method is more numerically stable when the plane is far away from origin, because the LLS method would require more digits after decimal to be stored and processed in such cases.
• The LLS method can detect outliers by checking the dot product residual between each point and the estimated normal vector, whereas the SVD-based method can detect outliers by checking if the smallest eigenvalue of the covariance matrix is significantly smaller than the two larger eigenvalues (i.e. checking the shape of the covariance matrix).

We finally provide a test case in C++ and MATLAB.

// Test case in C++ (using LLS fitting method)
matA(0,0) = 5.4637; matA(0,1) = 10.3354; matA(0,2) = 2.7203;
matA(1,0) = 5.8038; matA(1,1) = 10.2393; matA(1,2) = 2.7354;
matA(2,0) = 5.8565; matA(2,1) = 10.2520; matA(2,2) = 2.3138;
matA(3,0) = 6.0405; matA(3,1) = 10.1836; matA(3,2) = 2.3218;
matA(4,0) = 5.5537; matA(4,1) = 10.3349; matA(4,2) = 1.8796;
// With this sample data, LLS fitting method can produce the following result
// fitted normal vector = (-0.0231143, -0.0838307, -0.00266429)
// unit normal vector = (-0.265682, -0.963574, -0.0306241)
// D = 11.4943

% Test case in MATLAB (using SVD-based method)
points = [5.4637 10.3354 2.7203;
          5.8038 10.2393 2.7354; 
          5.8565 10.2520 2.3138; 
          6.0405 10.1836 2.3218; 
          5.5537 10.3349 1.8796]
covariance = cov(points)
[V, D] = eig(covariance)
normal = V(:, 1) % pick the eigenvector that corresponds to the smallest eigenvalue
% normal = (0.2655, 0.9636, 0.0306)

Brachypterous