How to fix this permutation sort?

Question

The following Prolog program defines a predicate sorted/2 for sorting by permutation (permutation sort) in ascending order a list passed in first argument, which results in the list passed in second argument:

sorted(X, Y) :-
  permuted(X, Y),
  ordered(Y).

permuted([], []).
permuted(U, [V|W]) :-
  permuted(X, W),
  deleted(V, U, X).

deleted(X, [X|Y], Y).
deleted(U, [V|W], [V|X]) :-
  deleted(U, W, X).

ordered([]).
ordered([_]).
ordered([X, Y|Z]) :-
  ordered([Y|Z]), X =< Y.

How to solve the following issues?

1. The program duplicates solutions for queries in which a list with duplicate elements is passed in second argument:

?- sorted(X, [1, 1, 2]).
   X = [1, 1, 2]
;  X = [1, 1, 2]
;  X = [1, 2, 1]
;  X = [1, 2, 1]
;  X = [2, 1, 1]
;  X = [2, 1, 1]
;  false.

2. The program exhausts resources for queries in which a free variable is passed in second argument:

?- sorted([2, 1, 1], Y).
   Y = [1, 1, 2]
;  Y = [1, 1, 2]
;
Time limit exceeded

---

The Prolog program is based on the Horn clause program given at section 11 of Robert Kowalski’s famous paper Predicate Logic as Programming Language:

Eleazar

what are your predicates supposed to do? – Nat

One observation: both arguments are lists of same length. Thus add such a goal into sorted/2. – Inapproachable

@Inapproachable what will it achieve? – Nat

@Vulwsztyn: Termination – Inapproachable

See this for a related sorting. And the duplicates are very hard to remove if you insist on this exact approach. – Inapproachable

@Inapproachable Thanks, adding a samelength/2 goal to sorted/2 solves non-termination! If you want to write an answer I will accept it. – Carleycarli

See this how to remove duplicate solutions. – Inapproachable

@Inapproachable Perfect, thanks! – Carleycarli

Answer 1

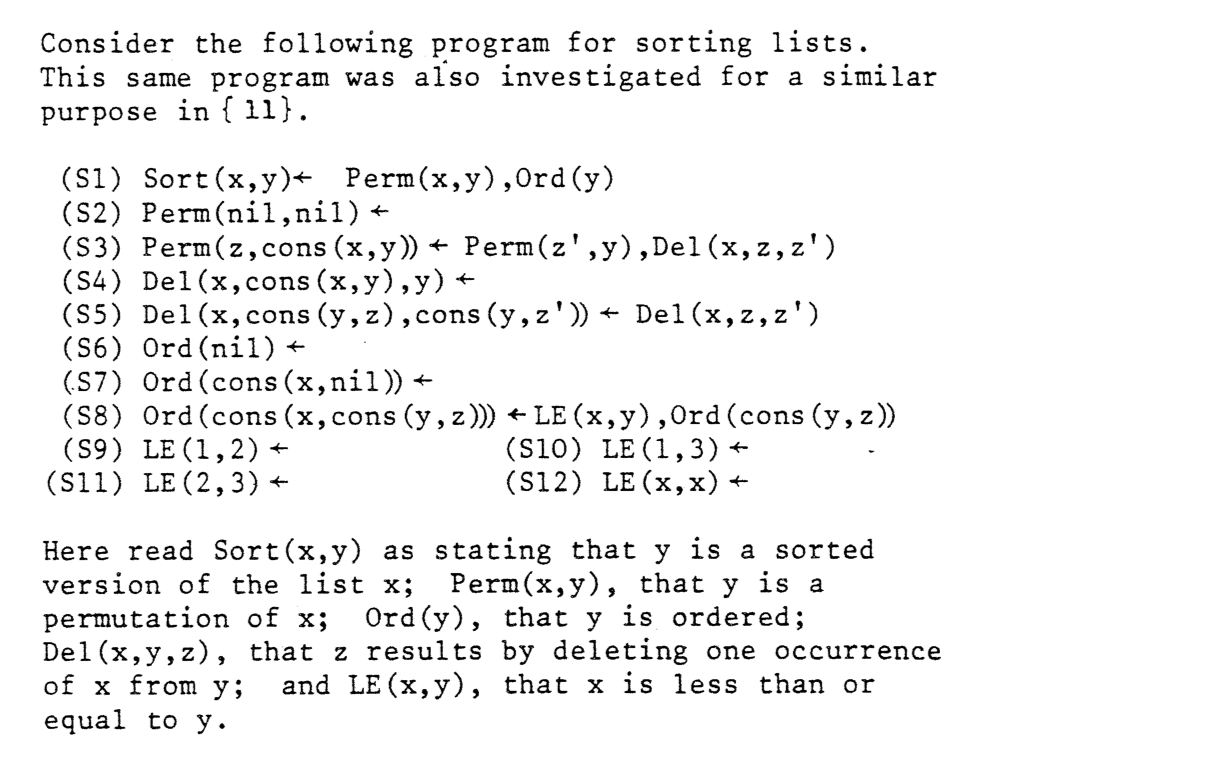
To solve non-termination, you can add same_length/2 to sorted/2 as @false suggested:

sorted(X, Y) :-
  same_length(X, Y),
  permuted(X, Y),
  ordered(Y).

same_length([], []).
same_length([_|Xs], [_|Ys]) :-
  same_length(Xs, Ys).

Or you may embed it into permuted/2 by adding a new argument:

sorted(X, Y) :-
  permuted(X, X, Y),
  ordered(Y).

permuted([], [], []).
permuted(U, [_|L1], [V|W]) :-
  permuted(X, L1, W),
  deleted(V, U, X).

The program will still return duplicates as it only sees one item at a time.

To solve duplication, you can either generate all permutations and discard the repeated ones (which is not efficient), or only generate distinct permutations. The following modification does the latter by taking the idea of the recursive procedure permuted/2 + deleted/2 which for each item puts it at the beginning of the list and does a recursive call on the remaining list, and changes it to another recursive procedure permuted_all/2 + deleted_all/2 which for each group of same items puts them at the beginning of the list and does a recursive call on the remaining list. This program uses difference lists for better efficiency:

sorted(X, Y) :-
  same_length(X, Y),
  permuted_all(X, Y),
  ordered(Y).
    
permuted_all([], []).
permuted_all(U, [V|W]) :-
  deleted_all(V, U, X, n-T, [V|W]),
  permuted_all(X, T).
    
% deleted_all(Item, List, Remainder, n-T, Items|T)
deleted_all(_, [], [], y-[X|Xs], [X|Xs]).
deleted_all(X, [V|Y], [V|Y1], y-[X|Xs], Xs1) :-
  dif(X, V),
  deleted_all(X, Y, Y1, y-[X|Xs], Xs1).
deleted_all(X, [X|Y], Y1, _-Xs, Xs1) :-
  deleted_all(X, Y, Y1, y-[X|Xs], Xs1).
deleted_all(U, [V|W], [V|X], n-T, Xs) :-
  dif(U, V),
  deleted_all(U, W, X, n-T, Xs).

Sample runs:

?- sorted(X, [1, 1, 2]).
   X = [1, 2, 1]
;  X = [1, 1, 2]
;  X = [2, 1, 1]
;  false.

?- sorted([2, 1, 1], Y).
   Y = [1, 1, 2]
;  false.

---

As per OPs comment asking for a version which does not use difference lists, here goes one which instead obtains the remainder using same_length/2 + append/3 and with added comments:

permuted_all([], []).
permuted_all(U, [V|W]) :-
  deleted_all(V, U, X, n, [V|W]),
  same_length(X, T),    % the remaining list X has the same length as T
  append(_, T, [V|W]),  % T corresponds to the last items of [V|W]
  permuted_all(X, T).   % T is a permutation of X
    
% deleted_all(Item, List, Remainder, n, Items|_)
deleted_all(_, [], [], y, _).  % base case
deleted_all(X, [V|Y], [V|Y1], y, Xs1) :-
  % recursive step when the current item is not the one we are gathering
  dif(X, V),
  deleted_all(X, Y, Y1, y, Xs1).
deleted_all(X, [X|Y], Y1, _, [X|Xs1]) :-
  % recursive step when the current item is the one we are gathering
  deleted_all(X, Y, Y1, y, Xs1).
deleted_all(U, [V|W], [V|X], n, Xs) :-
  % recursive step when we have not selected yet the item we will be gathering
  dif(U, V),
  deleted_all(U, W, X, n, Xs).

Ferrous

Thanks Gustavo! What do n-T and Items|T mean? – Carleycarli

I am using the atom n to avoid the procedure to succeed with List and Reminder being empty lists. So at least one of them must be not empty. – Ferrous

I am using difference lists to avoid needing to use append/3 to split the List into the list of deleted Item and the rest of the permuted list. So when I pass n-T to deleted_all/5 the last argument will hold the selected item (possibly repeated N times) with the tail of that list being T, which will be further used to complete recursion. – Ferrous

I am still struggling to understand this part. The original predicate permuted/2 does a permutation of a list using a recursive rule definition: a list U has a permutation [V|W] if W is a permutation of the list resulting from deleting the first occurence of V from U. What does the new predicate permuted_all/2 do in plain English? – Carleycarli

Let me try to word it in plain english: a list U has a permutation [V|W] where W is a permutation of the list resulting from deleting one occurence of V from U and having any other occurence of V before any other element which is not V. So if U has N (N>0) occurences of V then [U|W] will be permutations of U that begin with N Vs – Ferrous

I see, so for instance if U is [2, 1, 2], while permuted/2 computes the permutations [2, 1, 2], [2, 2, 1], [1, 2, 2], [1, 2, 2], [2, 2, 1], [2, 1, 2], I expect permuted_all/2 to only compute the permutations [2, 2, 1], [2, 2, 1], [1, 2, 2], [1, 2, 2]. However that is not what I get, permuted_all/2 actually computes the permutations [2, 2, 1], [1, 2, 2], i.e. it also removes the duplicates. How does it do it? – Carleycarli

If U is [2, 1, 2] the first call to permuted_all/2 calls deleted_all/5 that will bind V with 2, [V|W] with [2,2|T] and X with [1]. Then the recursive call now calls deleted_all/5 which will bind V with 1, [V|W] with [1|T] and X with [] and you get the first solution ([2,2,1]). – Ferrous

Upon backtracking it will fall back through the alternative of the first call to deleted_all/5 which will now bind V with 1, [V|W] with [1|T] and X with [2,2]. Then, again, the recursive call is made which will bind V with 2, [V|W] with [2,2|T] and X with [] and you then get the second solution [1,2,2]. So the idea is that permutations are always done grouping all the ocuccurences of V from the current U. – Ferrous

So if U is [2, 1, 2], permuted/2 looks at each item and permutes the rest of the list (i.e. for item 2: [1, 2] and [2, 1], for item 1: [2, 2] and [2, 2], and for item 2: [2, 1] and [1, 2], resulting in the permutations [2, 1, 2], [2, 2, 1], [1, 2, 2], [1, 2, 2], [2, 2, 1], [2, 1, 2]), while permuted_all/2 looks at each set of items and permutes the rest of the list (i.e. for set of items [2, 2]: [1], and for set of item [1]: [2, 2] and [2, 2], resulting in the permutations [2, 2, 1], [1, 2, 2], [1, 2, 2]). Why a single [1, 2, 2] in the real result? – Carleycarli

I would not call it set because it usually implies no duplicates. Thats why I called them groups. The algorithm is recursive and applies the same idea to every group. So permuted_all/2 takes an item V and groups all items which are V together, then obtains the permutation of the remaining groups recursively. – Ferrous

So for the list L=[2,1,2] when it takes the group [2, 2] then continue with the recursion with the remaining list [1] which only has one permutation left ([1]). When it takes the group [1] then continues with the recursion with the remaining list [2, 2] which again only has one permutation left ([2, 2]). Therefore for the list [2, 1, 2] it compute two distinct solutions [1, 2, 2] and [2, 1, 1]. Then sorted/2 only succeeds for [1, 2, 2] which is the one sorted. – Ferrous

You are right, set is incorrect, the correct mathematical term is multiset (a.k.a. bag). permuted_all/2 actually generates all permutations of a multiset (the order in the input list is irrelevant so it can be considered as a multiset). And as you explained, it does this by taking each submultiset of identical items (that you called a group) and generating permutations with the remaining items. – Carleycarli

I get why for permuted_all/2 the group [2, 2] generates the permutation [1]. But I still don’t get why the group [1] generates a single permutation [2, 2] instead of two permutations [2, 2] and [2, 2] like for permuted/2. How do the extra 4th and 5th arguments of deleted_all/5 achieve this? As a beginner I am not familiar with difference lists (though I used this opportunity to learn about them) so if you could provide a program that does not rely on them that may help me to fully understand what is happening. – Carleycarli

The use of difference lists in this answer is only to improve efficency (avoiding to use append/3 between the calls to deleted_all/5 and permuted_all/2 to get the remaining part of the list). In the example, when you get the group [1] the remaining list [2, 2] generates only one permutation because the recursion calls permuted_all/2 whose productions are only unique groups of same-value items. – Ferrous

@Maggyero: added a commented version without difference lists at the end of the answer – Ferrous

I have finally got it after looking at the recursion as you suggested. permuted_all([2, 1, 2], X) takes each group of same items and does a recursive call on the rest of the list. So it initially takes the first group of same items [2, 2] from [2, 1, 2] and does a recursive call on [1], which takes the group of same items [1] from [1] and does a recursive call on [], which halts the computation and gives the first solution: [2, 2, 1]. – Carleycarli

… Then it takes the second group of same items [1] from [2, 1, 2] and does a recursive call on [2, 2], which takes the group of same items [2, 2] from [2, 2] and does a recursive call on [], which halts the computation and gives the second solution: [1, 2, 2]. – Carleycarli

@Maggyero: I have just rolled back your last changes to my answer because they are not what I expect from those procedures. I do not want to move same_length to where you moved them, they lead to useless computations. You may add another answer with your own changes (and accept your own answer instead of this one if you wish) – Ferrous

Actually I have edited your answer because permuted_all(X, [2, 1, 2]) does not terminate. – Carleycarli

permuted_all/2 is "internal" to sorted/2 which already takes care of that non-termination. You had also changed permuted/3 -> same_length/2+permuted/2 which processes the list every time – Ferrous

Okay, in other words we are optimizing permuted_all/2 by moving the call to same_length/2 outside the procedure. That makes sense for an internal procedure. So I have just restored the non controversial part which will hopefully improve this excellent answer. – Carleycarli

By the way Gustavo, do you know a way to embed same_length/2 into permuted_all/2 like you did for permuted/2? – Carleycarli

You would probably need to embed it from sorted/2 all the way down to deleted_all/5 due to the interleaved recursion. – Ferrous

Alright. I am trying but I didn’t find a way yet. – Carleycarli

Answer 2

Your second problem can by solved by replacing first line with

sorted(X, Y) :-
  permuted(X, Y),
  ordered(Y),
  !.

or

sorted(X, Y) :-
  permuted(X, Y),
  ordered(Y),
  length(X, Z),
  length(Y, Z).

The first one is not so easy to solve because of the implementation of this algorithm. Both 1st [1, 1, 2] and 2nd [1, 1, 2] are valid permutations since your code that generated permutations generates all permutations not unique permutations.

Nat

Thanks. Note that cuts should be avoided. – Carleycarli

@Maggyero Yes but also permutation sort should be avoided. On a scale of 1 to 10 implementing a permutations sort is kinda silly. – Jeans

@Jeans I agree, but that was not intended for production, only for reproducing the program of an academic paper. – Carleycarli