Matlab: xcorr 1d cross-correlation normalisation issue

Question

I have a reference signal (s1) of length = 5 and another signal (s2) of length = 25 samples (containing a shifted version of the same 5 sample signal s1).

I want to find the normalised cross correlation between the two signals to calculate the sample distance (delay / lag) between signals s1 and s2.

I pad s1 with zeros (so it is the same length as s2 as required for xcorr 'coeff' option):

s1(numel(s2)) = 0;

and then do:

[R lags]=xcorr(s2,s1,'coeff');

[vm im]=max(R); %max. correlation and index
s1_lag=lags(im);

to find the normalised cross-correlation for lags of -24 to 24 samples.

Since s2 contains a shifted version of s1 I would expect to obtain a maximum correlation value of 1 but maximum correlation is 0.4776 at a lag of 19 samples. I don't understand this?

If I let s1 = s2 and repeat xcorr (now s1 and s2 are identical) I get a maximum correlation value of 1.0 at 0 sample lag as expected.

Djerba

Review my update for your point max correlation=1 if s2 contains an identical segment – Calomel

Answer 1

The delay corresponds to the max peak value (but not necessarily 1 ( 1 will be the value of xcorr between the same vector - auto correlation at leg 0) and two opposite signals will have value of -1).

xcorr provides normalization scheme. The syntax xcorr(x,y,'coeff')

divides the output by norm(x)*norm(y) so that, for auto-correlations, the sample at zero lag is 1.

http://matlab.izmiran.ru/help/toolbox/signal/spectra3.html

The following code compute xcorr for the two signal as OP, with delay 5:

    % s1) of length = 5 and another signal (s2) of length = 25
    s1=[1 2 3 4 5]
    s2=[0 0 0 0 0  s1  1 1 2 3 1 5  2 3 2 4 1 ]

    s1(numel(s2)) = 0;
    s1

    [R lags]=xcorr(s2,s1,'coeff');

    [vm im]=max(R) %max. correlation and index
    s1_lag=lags(im)
   % review the plot
   figure
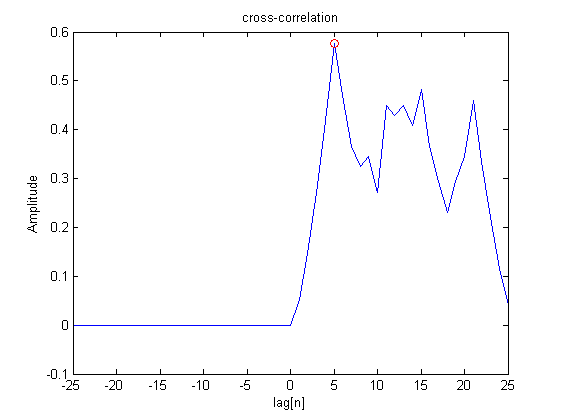
  plot(lags,R), hold on,plot(s1_lag,vm,'ro'),ylabel('Amplitude'),xlabel('lag[n]');
title('cross-correlation');

 % result
 %vm =   0.5756
 %im =  31
 %s1_lag = 5

The result is:

Max =  0.5756 (need not to be 1, but it is the peak value)
delay = 5 ( match the actual delay between the two signal which is 5)

The plot of xcorr

Update:

For signals of unequal length and padding the shorter with zeros, normalization in xcorr has no meaning.

You can use xcorr (s1,s2,'none') or xcorr (s1,s2 ) and xcor internally pads the shorter signal with zeros for equal length.

You get the the position of peak value which indicates the time offset at which the two signals are the most similar. in our example, using xcorr (s1,s2,'none'), the result is: vm = 55.0000
s1_lag = 5

In Matlab there is a function named : alignsignals can be used with xcorr as in the following code:

    % method 2: align signals and xcorr for the new aligned signals . 
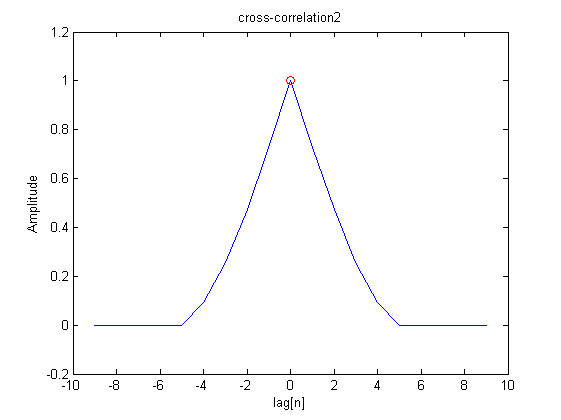
    %in that case you get  max of xcor  = 1, delay =0
    [Xa,Ya] = alignsignals(s2,s1)

     % after aligning signals, take the part of signal Xa with equal lentht of Ya
     [R2 lags2]=xcorr(Xa(1:length(Ya)),Ya,'coeff');
      [vm2 im2]=max(R2) %max. correlation and index
        s1_lag2=lags2(im2)

      figure
      plot(lags2,R2), hold on,plot(s1_lag2,vm2,'ro'),ylabel('Amplitude'),xlabel('lag[n]');
      title('cross-correlation2');

The following plot is the resultant xcorr :

The alligned signals

 Xa =    0     0     0     0     0     1     2     3     4     5     1     1     2     3     1     5    2     3     2     4     1


Ya =     0     0     0     0     0     1     2     3     4     5

Calomel

Thanks i understand but is a modification possible to normalisation so max correlation =1 if s2 contains an identical segment of s1. I.e in your example. – Djerba

I think this is the way normxcorr2 works for 2d template matching – Djerba

Review my update for your point max correlation=1 if s2 contains an identical segment – Calomel

I don't have function {alignsignals}. I think that's in a newer matlab version but I think it would be possible to write my own script to do this with only xcorr and padding. I am surprise there is no 1d equivalent of normxcorr2 in matlab. – Djerba

function {alignsignals} is available in MATLAB Release: R13 – Calomel