strange output in comparison of float with float literal

Question

float f = 0.7;
if( f == 0.7 )
    printf("equal");
else
    printf("not equal");

Why is the output not equal ?

Why does this happen?

Oospore

see https://mcmap.net/q/392663/-float-addition-promoted-to-double and #1839725, for instance.. – Corned

Wow, this is the third C/C++ question in a row about floating point precision. See https://mcmap.net/q/392663/-float-addition-promoted-to-double and #1839725 – Remindful

Read "What Every Computer Scientist Should Know About Floating-Point Arithmetic" [ docs.sun.com/source/806-3568/ncg_goldberg.html ] – Hamforrd

Everyone saw the first question and started experimenting with what other weirdness they can get? – Libelant

Note that the Sun URL for WECSSKAFPA now ends at an Oracle web site (since Oracle bought Sun). – Marti

Enable compiler warnings: warning C4305: 'initializing' : truncation from 'double' to 'float' – Autolysis

0.7 is not a "float literal", it's a double. – Sunbow

Answer 1

This happens because in your statement

  if(f == 0.7)

the 0.7 is treated as a double. Try 0.7f to ensure the value is treated as a float:

  if(f == 0.7f)

But as Michael suggested in the comments below you should never test for exact equality of floating-point values.

Nightcap

Yes. The f suffix (as in 0.7f) makes them a float literal. – Dairy

Perhaps more importantly, don't test for exact equality of floating-point values. – Hock

Yes, Michael has proposed the best answer here. You should never be looking for equality between floating point numbers. This answer will only lead to more confusion later on. – Boatbill

“don't test for equality of floating-point values” is based only in superstition. There is a reason why integers overflow. As a programmer, one does not abandon the path of reason and declare “it's useless trying to compute with integers, they can overflow”. One learns how integers work and how to use them properly. It's the same for floating-point. There are reasons why a floating-point computation may be exact or may not be. The reasons are not difficult to understand. Testing equality makes sense in some cases. – Ferreira

Answer 2

This answer to complement the existing ones: note that 0.7 is not representable exactly either as a float (or as a double). If it was represented exactly, then there would be no loss of information when converting to float and then back to double, and you wouldn't have this problem.

It could even be argued that there should be a compiler warning for literal floating-point constants that cannot be represented exactly, especially when the standard is so fuzzy regarding whether the rounding will be made at run-time in the mode that has been set as that time or at compile-time in another rounding mode.

All non-integer numbers that can be represented exactly have 5 as their last decimal digit. Unfortunately, the converse is not true: some numbers have 5 as their last decimal digit and cannot be represented exactly. Small integers can all be represented exactly, and division by a power of 2 transforms a number that can be represented into another that can be represented, as long as you do not enter the realm of denormalized numbers.

Ferreira

"Small integers" needs to be defined here - a IEEE float will hold 24 bits without loss, or up to 16777215. A double hold 54 bits which is much larger than a standard int. – Bottle

@MarkRansom: to a mathematician, all integers smaller than any fixed bound are "small". Also, 53 bits. – Hewie

@StephenCanon, thanks for the correction, I knew it was 53 bits so I plead temporary insanity. – Bottle

"All non-integer numbers that can be represented exactly have 5 as their last decimal." . Every day I learn something new. This was that thing today. Thanks! – Bravura

@Bravura - Any decimal that can be converted to a fraction that has a power of 2 as a denominator can be represented exactly. All such fractions will end in 5 because the denominator in a decimal is going to be a power of 10, and you have to divide 10 by 5 to get 2 and so the numerator will have to be divisible by 5 at least once. – Jovitta

Answer 3

First of all let look inside float number. I take 0.1f it is 4 byte long (binary32), in hex it is
3D CC CC CD.
By the standart IEEE 754 to convert it to decimal we must do like this:

In binary 3D CC CC CD is
0 01111011 1001100 11001100 11001101
here first digit is a Sign bit. 0 means (-1)^0 that our number is positive.
Second 8 bits is an Exponent. In binary it is 01111011 - in decimal 123. But the real Exponent is 123-127 (always 127)=-4, it's mean we need to multiply the number we will get by 2^ (-4).
The last 23 bytes is the Significand precision. There the first bit we multiply by 1/ (2^1) (0.5), second by 1/ (2^2) (0.25) and so on. Here what we get:

We need to add all numbers (power of 2) and add to it 1 (always 1, by standart). It is
1,60000002384185791015625
Now let's multiply this number by 2^ (-4), it's from Exponent. We just devide number above by 2 four time:
0,100000001490116119384765625
I used MS Calculator


**

Now the second part. Converting from decimal to binary.

**
I take the number 0.1
It ease because there is no integer part. First Sign bit - it is 0. Exponent and Significand precision I will calculate now. The logic is multiply by 2 whole number (0.1*2=0.2) and if it's bigger than 1 substract and continue.

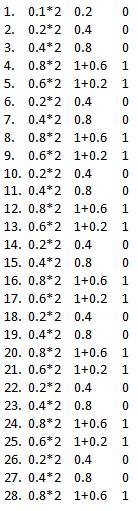
And the number is .00011001100110011001100110011, standart says that we must shift left before we get 1. (something). How you see we need 4 shifts, from this number calculating Exponent (127-4=123). And the Significand precision now is
10011001100110011001100 (and there is lost bits).
Now the whole number. Sign bit 0 Exponent is 123 (01111011) and Significand precision is 10011001100110011001100 and whole it is
00111101110011001100110011001100 let's compare it with those we have from previous chapter
00111101110011001100110011001101
As you see the lasts bit are not equal. It is because I truncate the number. The CPU and compiler know that the is something after Significand precision can not hold and just set the last bit to 1.

Adolescence

how does 0.5 comparison not work even if its mantissa fits in this format ? – Quilting

Answer 4

Another near exact question was linked to this one, thus the years late answer. I don't think the above answers are complete.

int fun1 ( void )
{
      float x=0.7;
      if(x==0.7) return(1);
      else       return(0);
}
int fun2 ( void )
{
      float x=1.1;
      if(x==1.1) return(1);
      else       return(0);
}
int fun3 ( void )
{
      float x=1.0;
      if(x==1.0) return(1);
      else       return(0);
}
int fun4 ( void )
{
      float x=0.0;
      if(x==0.0) return(1);
      else       return(0);
}
int fun5 ( void )
{
      float x=0.7;
      if(x==0.7f) return(1);
      else       return(0);
}
float fun10 ( void )
{
    return(0.7);
}
double fun11 ( void )
{
    return(0.7);
}
float fun12 ( void )
{
    return(1.0);
}
double fun13 ( void )
{
    return(1.0);
}

Disassembly of section .text:

00000000 <fun1>:
   0:   e3a00000    mov r0, #0
   4:   e12fff1e    bx  lr

00000008 <fun2>:
   8:   e3a00000    mov r0, #0
   c:   e12fff1e    bx  lr

00000010 <fun3>:
  10:   e3a00001    mov r0, #1
  14:   e12fff1e    bx  lr

00000018 <fun4>:
  18:   e3a00001    mov r0, #1
  1c:   e12fff1e    bx  lr

00000020 <fun5>:
  20:   e3a00001    mov r0, #1
  24:   e12fff1e    bx  lr

00000028 <fun10>:
  28:   e59f0000    ldr r0, [pc]    ; 30 <fun10+0x8>
  2c:   e12fff1e    bx  lr
  30:   3f333333    svccc   0x00333333

00000034 <fun11>:
  34:   e28f1004    add r1, pc, #4
  38:   e8910003    ldm r1, {r0, r1}
  3c:   e12fff1e    bx  lr
  40:   66666666    strbtvs r6, [r6], -r6, ror #12
  44:   3fe66666    svccc   0x00e66666

00000048 <fun12>:
  48:   e3a005fe    mov r0, #1065353216 ; 0x3f800000
  4c:   e12fff1e    bx  lr

00000050 <fun13>:
  50:   e3a00000    mov r0, #0
  54:   e59f1000    ldr r1, [pc]    ; 5c <fun13+0xc>
  58:   e12fff1e    bx  lr
  5c:   3ff00000    svccc   0x00f00000  ; IMB

Why did fun3 and fun4 return one and not the others? why does fun5 work?

It is about the language. The language says that 0.7 is a double unless you use this syntax 0.7f then it is a single. So

  float x=0.7;

the double 0.7 is converted to a single and stored in x.

  if(x==0.7) return(1);

The language says we have to promote to the higher precision so the single in x is converted to a double and compared with the double 0.7.

00000028 <fun10>:
  28:   e59f0000    ldr r0, [pc]    ; 30 <fun10+0x8>
  2c:   e12fff1e    bx  lr
  30:   3f333333    svccc   0x00333333

00000034 <fun11>:
  34:   e28f1004    add r1, pc, #4
  38:   e8910003    ldm r1, {r0, r1}
  3c:   e12fff1e    bx  lr
  40:   66666666    strbtvs r6, [r6], -r6, ror #12
  44:   3fe66666    svccc   0x00e66666

single 3f333333 double 3fe6666666666666

As Alexandr pointed out if that answer remains IEEE 754 a single is

seeeeeeeefffffffffffffffffffffff

And double is

seeeeeeeeeeeffffffffffffffffffffffffffffffffffffffffffffffffffff

with 52 bits of fraction rather than the 23 that single has.

00111111001100110011... single
001111111110011001100110... double

0 01111110 01100110011... single
0 01111111110 01100110011... double

Just like 1/3rd in base 10 is 0.3333333... forever. We have a repeating pattern here 0110

01100110011001100110011 single, 23 bits
01100110011001100110011001100110.... double 52 bits.

And here is the answer.

  if(x==0.7) return(1);

x contains 01100110011001100110011 as its fraction, when that gets converted back to double the fraction is

01100110011001100110011000000000....

which is not equal to

01100110011001100110011001100110...

but here

  if(x==0.7f) return(1);

That promotion doesn't happen the same bit patterns are compared with each other.

Why does 1.0 work?

00000048 <fun12>:
  48:   e3a005fe    mov r0, #1065353216 ; 0x3f800000
  4c:   e12fff1e    bx  lr

00000050 <fun13>:
  50:   e3a00000    mov r0, #0
  54:   e59f1000    ldr r1, [pc]    ; 5c <fun13+0xc>
  58:   e12fff1e    bx  lr
  5c:   3ff00000    svccc   0x00f00000  ; IMB

0011111110000000...
0011111111110000000...

0 01111111 0000000...
0 01111111111 0000000...

In both cases the fraction is all zeros. So converting from double to single to double there is no loss of precision. It converts from single to double exactly and the bit comparison of the two values works.

The highest voted and checked answer by halfdan is the correct answer, this is a case of mixed precision AND you should never do an equals comparison.

The why wasn't shown in that answer. 0.7 fails 1.0 works. Why did 0.7 fail wasn't shown. A duplicate question 1.1 fails as well.

---

Edit

The equals can be taken out of the problem here, it is a different question that has already been answered, but it is the same problem and also has the "what the ..." initial shock.

int fun1 ( void )
{
      float x=0.7;
      if(x<0.7) return(1);
      else       return(0);
}
int fun2 ( void )
{
      float x=0.6;
      if(x<0.6) return(1);
      else       return(0);
}

Disassembly of section .text:

00000000 <fun1>:
   0:   e3a00001    mov r0, #1
   4:   e12fff1e    bx  lr

00000008 <fun2>:
   8:   e3a00000    mov r0, #0
   c:   e12fff1e    bx  lr

Why does one show as less than and the other not less than? When they should be equal.

From above we know the 0.7 story.

01100110011001100110011 single, 23 bits
01100110011001100110011001100110.... double 52 bits.

01100110011001100110011000000000....

is less than.

01100110011001100110011001100110...

0.6 is a different repeating pattern 0011 rather than 0110.

but when converted from a double to a single or in general when represented as a single IEEE 754.

00110011001100110011001100110011.... double 52 bits.
00110011001100110011001 is NOT the fraction for single
00110011001100110011010 IS the fraction for single

IEEE 754 uses rounding modes, round up, round down or round to zero. Compilers tend to round up by default. If you remember rounding in grade school 12345678 if I wanted to round to the 3rd digit from the top it would be 12300000 but round to the next digit 1235000 if the digit after is 5 or greater then round up. 5 is 1/2 of 10 the base (Decimal) in binary 1 is 1/2 of the base so if the digit after the position we want to round is 1 then round up else don't. So for 0.7 we didn't round up, for 0.6 we do round up.

And now it is easy to see that

00110011001100110011010

converted to a double because of (x<0.7)

00110011001100110011010000000000....

is greater than

00110011001100110011001100110011....

So without having to talk about using equals the issue still presents itself 0.7 is double 0.7f is single, the operation is promoted to the highest precision if they differ.

Risser

Answer 5

The problem you're facing is, as other commenters have noted, that it's generally unsafe to test for exact equivalency between floats, as initialization errors, or rounding errors in calculations can introduce minor differences that will cause the == operator to return false.

A better practice is to do something like

float f = 0.7;
if( fabs(f - 0.7) < FLT_EPSILON )
    printf("equal");
else
    printf("not equal");

Assuming that FLT_EPSILON has been defined as an appropriately small float value for your platform.

Since the rounding or initialization errors will be unlikely to exceed the value of FLT_EPSILON, this will give you the reliable equivalency test you're looking for.

Beefwitted

Answer 6

A lot of the answers around the web make the mistake of looking at the abosulute difference between floating point numbers, this is only valid for special cases, the robust way is to look at the relative difference as in below:

      // Floating point comparison:

        bool CheckFP32Equal(float referenceValue, float value)
        {
           const float fp32_epsilon = float(1E-7);
           float abs_diff = std::abs(referenceValue - value);

           // Both identical zero is a special case
           if( referenceValue==0.0f && value == 0.0f)
              return true;

           float rel_diff = abs_diff / std::max(std::abs(referenceValue) , std::abs(value) ); 

           if(rel_diff < fp32_epsilon)
                 return true;
           else 
                 return false;

        }

Erysipeloid

Answer 7

Consider this:

int main()
{
    float a = 0.7;
    if(0.7 > a)
        printf("Hi\n");
    else
        printf("Hello\n");
    return 0;
}

if (0.7 > a) here a is a float variable and 0.7 is a double constant. The double constant 0.7 is greater than the float variable a. Hence the if condition is satisfied and it prints 'Hi'

Example:

int main()
{
    float a=0.7;
    printf("%.10f %.10f\n",0.7, a);
    return 0;
}

Output:
0.7000000000 0.6999999881

Lungworm

Answer 8

Pointing value saved in variable and constant have not same data types. It's the difference in the precision of data types. If you change the datatype of f variable to double, it'll print equal, This is because constants in floating-point stored in double and non-floating in long by default, double's precision is higher than float. it'll be completely clear if you see the method of floating-point numbers conversion to binary conversion

Doyen