The simplest way I see to fulfill all your requirements:
- Constant-time insertion/removal (hope amortized constant-time is okay for insertion).
- No heap allocation/deallocation per element.
- No iterator invalidation on removal.
... would be something like this, just making use of std::vector:
template <class T>
struct Node
{
// Stores the memory for an instance of 'T'.
// Use placement new to construct the object and
// manually invoke its dtor as necessary.
typename std::aligned_storage<sizeof(T), alignof(T)>::type element;
// Points to the next element or the next free
// element if this node has been removed.
int next;
// Points to the previous element.
int prev;
};
template <class T>
class NodeIterator
{
public:
...
private:
std::vector<Node<T>>* nodes;
int index;
};
template <class T>
class Nodes
{
public:
...
private:
// Stores all the nodes.
std::vector<Node> nodes;
// Points to the first free node or -1 if the free list
// is empty. Initially this starts out as -1.
int free_head;
};
... and hopefully with a better name than Nodes (I'm slightly tipsy and not so good at coming up with names at the moment). I'll leave the implementation up to you but that's the general idea. When you remove an element, just do a doubly-linked list removal using the indices and push it to the free head. The iterator doesn't invalidate since it stores an index to a vector. When you insert, check if the free head is -1. If not, overwrite the node at that position and pop. Otherwise push_back to the vector.
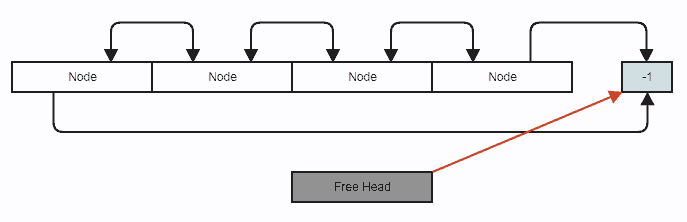
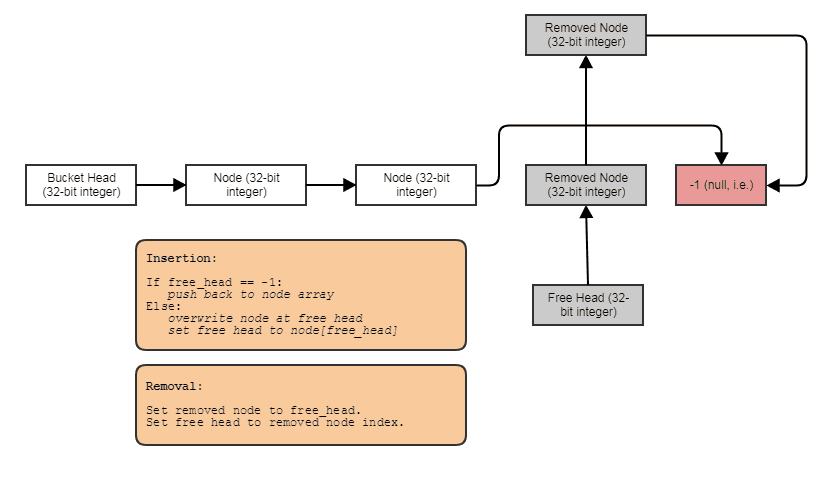
Illustration
Diagram (nodes are stored contiguously inside std::vector, we simply use index links to allow skipping over elements in a branchless way along with constant-time removals and insertions anywhere):
![enter image description here]()
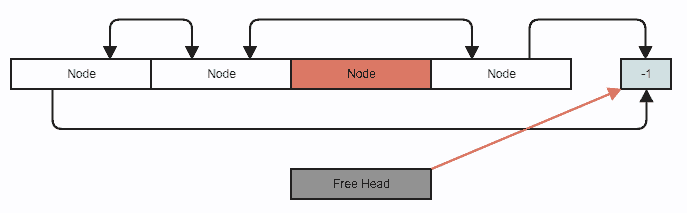
Let's say we want to remove a node. This is your standard doubly-linked list removal, except we use indices instead of pointers and you also push the node to the free list (which just involves manipulating integers):
Removal adjustment of links:
![enter image description here]()
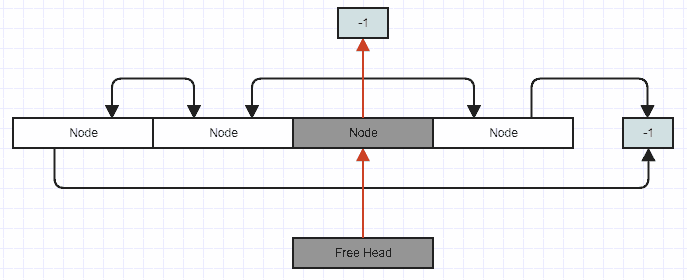
Pushing removed node to free list:
![enter image description here]()
Now let's say you insert to this list. In that case, you pop off the free head and overwrite the node at that position.
After insertion:
![enter image description here]()
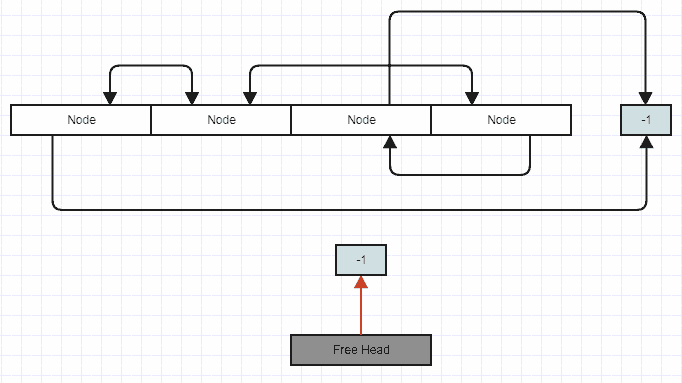
Insertion to the middle in constant-time should likewise be easy to figure out. Basically you just insert to the free head or push_back to the vector if the free stack is empty. Then you do your standard double-linked list insertion. Logic for the free list (though I made this diagram for someone else and it involves an SLL, but you should get the idea):
![enter image description here]()
Make sure you properly construct and destroy the elements using placement new and manual calls to the dtor on insertion/removal. If you really want to generalize it, you'll also need to think about exception-safety and we also need a read-only const iterator.
Pros and Cons
The benefit of such a structure is that it does allow very rapid insertions/removals from anywhere in the list (even for a gigantic list), insertion order is preserved for traversal, and it never invalidates the iterators to element which aren't directly removed (though it will invalidate pointers to them; use deque if you don't want pointers to be invalidated). Personally I'd find more use for it than std::list (which I practically never use).
For large enough lists (say, larger than your entire L3 cache as a case where you should definitely expect a huge edge), this should vastly outperform std::vector for removals and insertions to/from the middle and front. Removing elements from vector can be quite fast for small ones, but try removing a million elements from a vector starting from the front and working towards the back. There things will start to crawl while this one will finish in the blink of an eye. std::vector is ever-so-slightly overhyped IMO when people start using its erase method to remove elements from the middle of a vector spanning 10k elements or more, though I suppose this is still preferable over people naively using linked lists everywhere in a way where each node is individually allocated against a general-purpose allocator while causing cache misses galore.
The downside is that it only supports sequential access, requires the overhead of two integers per element, and as you can see in the above diagram, its spatial locality degrades if you constantly remove things sporadically.
Spatial Locality Degradation
The loss of spatial locality as you start removing and inserting a lot from/to the middle will lead to zig-zagging memory access patterns, potentially evicting data from a cache line only to go back and reload it during a single sequential
loop. This is generally inevitable with any data structure that allows removals from the middle in constant-time while likewise allowing that space to be reclaimed while preserving the order of insertion. However, you can restore spatial locality by offering some method or you can copy/swap the list. The copy constructor can copy the list in a way that iterates through the source list and inserts all the elements which gives you back a perfectly contiguous, cache-friendly vector with no holes (though doing this will invalidate iterators).
Alternative: Free List Allocator
An alternative that meets your requirements is implement a free list conforming to std::allocator and use it with std::list. I never liked reaching around data structures and messing around with custom allocators though and that one would double the memory use of the links on 64-bit by using pointers instead of 32-bit indices, so I'd prefer the above solution personally using std::vector as basically your analogical memory allocator and indices instead of pointers (which both reduce size and become a requirement if we use std::vector since pointers would be invalidated when vector reserves a new capacity).
Indexed Linked Lists
I call this kind of thing an "indexed linked list" as the linked list isn't really a container so much as a way of linking together things already stored in an array. And I find these indexed linked lists exponentially more useful since you don't have to get knee-deep in memory pools to avoid heap allocations/deallocations per node and can still maintain reasonable locality of reference (great LOR if you can afford to post-process things here and there to restore spatial locality).
You can also make this singly-linked if you add one more integer to the node iterator to store the previous node index (comes free of memory charge on 64-bit assuming 32-bit alignment requirements for int and 64-bit for pointers). However, you then lose the ability to add a reverse iterator and make all iterators bidirectional.
Benchmark
I whipped up a quick version of the above since you seem interested in 'em: release build, MSVC 2012, no checked iterators or anything like that:
--------------------------------------------
- test_vector_linked
--------------------------------------------
Inserting 200000 elements...
time passed for 'inserting': {0.000015 secs}
Erasing half the list...
time passed for 'erasing': {0.000021 secs}
time passed for 'iterating': {0.000002 secs}
time passed for 'copying': {0.000003 secs}
Results (up to 10 elements displayed):
[ 11 13 15 17 19 21 23 25 27 29 ]
finished test_vector_linked: {0.062000 secs}
--------------------------------------------
- test_vector
--------------------------------------------
Inserting 200000 elements...
time passed for 'inserting': {0.000012 secs}
Erasing half the vector...
time passed for 'erasing': {5.320000 secs}
time passed for 'iterating': {0.000000 secs}
time passed for 'copying': {0.000000 secs}
Results (up to 10 elements displayed):
[ 11 13 15 17 19 21 23 25 27 29 ]
finished test_vector: {5.320000 secs}
Was too lazy to use a high-precision timer but hopefully that gives an idea of why one shouldn't use vector's linear-time erase method in critical paths for non-trivial input sizes with vector above there taking ~86 times longer (and exponentially worse the larger the input size -- I tried with 2 million elements originally but gave up after waiting almost 10 minutes) and why I think vector is ever-so-slightly-overhyped for this kind of use. That said, we can turn removal from the middle into a very fast constant-time operation without shuffling the order of the elements, without invalidating indices and iterators storing them, and while still using vector... All we have to do is simply make it store a linked node with prev/next indices to allow skipping over removed elements.
For removal I used a randomly shuffled source vector of even-numbered indices to determine what elements to remove and in what order. That somewhat mimics a real world use case where you're removing from the middle of these containers through indices/iterators you formerly obtained, like removing the elements the user formerly selected with a marquee tool after he his the delete button (and again, you really shouldn't use scalar vector::erase for this with non-trivial sizes; it'd even be better to build a set of indices to remove and use remove_if -- still better than vector::erase called for one iterator at a time).
Note that iteration does become slightly slower with the linked nodes, and that doesn't have to do with iteration logic so much as the fact that each entry in the vector is larger with the links added (more memory to sequentially process equates to more cache misses and page faults). Nevertheless, if you're doing things like removing elements from very large inputs, the performance skew is so epic for large containers between linear-time and constant-time removal that this tends to be a worthwhile exchange.

std::vectorso that they are sorted, outperforms all other contains up to 500,000 elelemts (it's more but that is where they stopped testing) – Raymundoraynastd::list. – Atlantesstd::listdue to poor memory locality and a lot of indirection. A custom allocator might help, but it can’t give you locality if you keep inserting in the middle. – Jeniferstd::vector) and access patterns that the prefetcher can predict easily. They really don't like chasing pointers all over memory (std::list). That's whystd::vectorusually outperformsstd::listin real life, regardless of theoretical complexity. – CordiacordialO(1)insert, when sometimesO(n)might be faster. It's possible forK * 1to be larger thank * n.std::vectorhas a very smallk. – Afterwards