What's the difference between pandas ACF and statsmodel ACF?

Question

I'm calculating the Autocorrelation Function for a stock's returns. To do so I tested two functions, the autocorr function built into Pandas, and the acf function supplied by statsmodels.tsa. This is done in the following MWE:

import pandas as pd
from pandas_datareader import data
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta
from statsmodels.tsa.stattools import acf, pacf

ticker = 'AAPL'
time_ago = datetime.datetime.today().date() - relativedelta(months = 6)

ticker_data = data.get_data_yahoo(ticker, time_ago)['Adj Close'].pct_change().dropna()
ticker_data_len = len(ticker_data)

ticker_data_acf_1 =  acf(ticker_data)[1:32]
ticker_data_acf_2 = [ticker_data.autocorr(i) for i in range(1,32)]

test_df = pd.DataFrame([ticker_data_acf_1, ticker_data_acf_2]).T
test_df.columns = ['Pandas Autocorr', 'Statsmodels Autocorr']
test_df.index += 1
test_df.plot(kind='bar')

What I noticed was the values they predicted weren't identical:

What accounts for this difference, and which values should be used?

Overexert

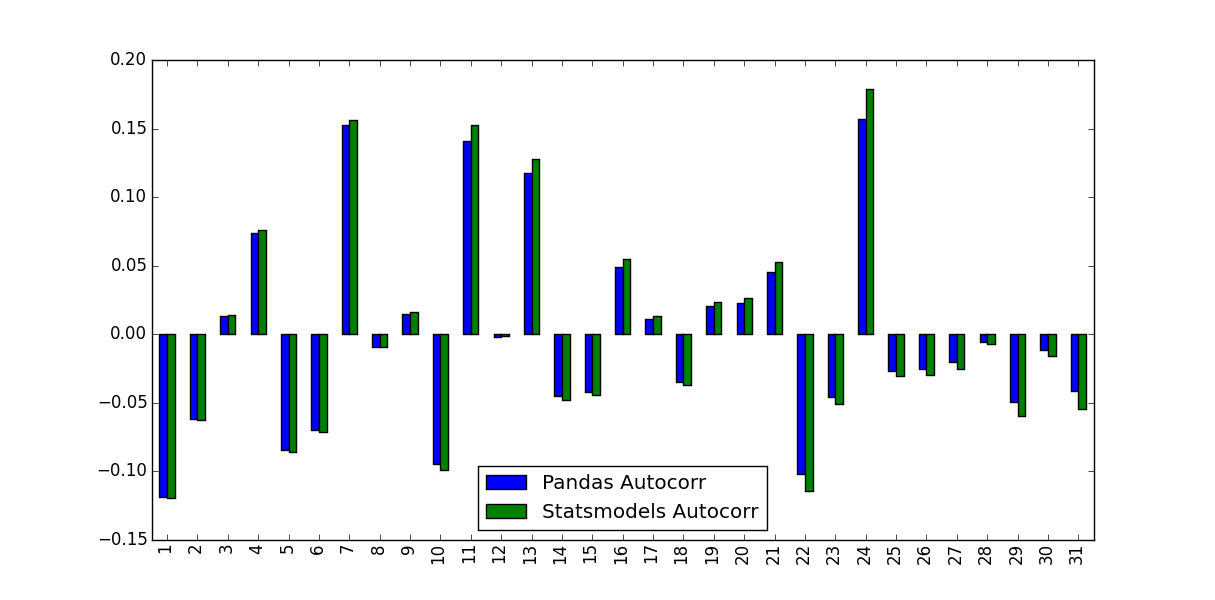
Looking at the docs the default lags is 1 for the pandas version and 40 for statsmodel – Kraemer

Try unbiased=True as option to the statsmodels version. – Kelsey

You reversed the labels in your plot, I think unbiased=True should make the autocorrelation coefficients larger. – Kelsey

autocorr from pandas is calling numpy.corrcoef while acf from statsmodels is calling numpy.correlate. I think digging in those can help to find the root of the differences in the outputs. – Vries

Is the first comment here an answer to the question? It would be great to have this one resolved – Ronaldronalda

It must be some kind of normalization issue, as discussed here: #5639780 – Pruinose

@Ronaldronalda the second and third comments were answers – Yahwistic

Answer 1

The difference between the Pandas and Statsmodels version lie in the mean subtraction and normalization / variance division:

• autocorr does nothing more than passing subseries of the original series to np.corrcoef. Inside this method, the sample mean and sample variance of these subseries are used to determine the correlation coefficient
• acf, in contrary, uses the overall series sample mean and sample variance to determine the correlation coefficient.

The differences may get smaller for longer time series but are quite big for short ones.

Compared to Matlab, the Pandas autocorr function probably corresponds to doing Matlabs xcorr (cross-corr) with the (lagged) series itself, instead of Matlab's autocorr, which calculates the sample autocorrelation (guessing from the docs; I cannot validate this because I have no access to Matlab).

See this MWE for clarification:

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
plt.style.use("seaborn-colorblind")

def autocorr_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the subseries means
    sum_product = np.sum((y1-np.mean(y1))*(y2-np.mean(y2)))
    # Normalize with the subseries stds
    return sum_product / ((len(x) - lag) * np.std(y1) * np.std(y2))

def acf_by_hand(x, lag):
    # Slice the relevant subseries based on the lag
    y1 = x[:(len(x)-lag)]
    y2 = x[lag:]
    # Subtract the mean of the whole series x to calculate Cov
    sum_product = np.sum((y1-np.mean(x))*(y2-np.mean(x)))
    # Normalize with var of whole series
    return sum_product / ((len(x) - lag) * np.var(x))

x = np.linspace(0,100,101)

results = {}
nlags=10
results["acf_by_hand"] = [acf_by_hand(x, lag) for lag in range(nlags)]
results["autocorr_by_hand"] = [autocorr_by_hand(x, lag) for lag in range(nlags)]
results["autocorr"] = [pd.Series(x).autocorr(lag) for lag in range(nlags)]
results["acf"] = acf(x, unbiased=True, nlags=nlags-1)

pd.DataFrame(results).plot(kind="bar", figsize=(10,5), grid=True)
plt.xlabel("lag")
plt.ylim([-1.2, 1.2])
plt.ylabel("value")
plt.show()

Statsmodels uses np.correlate to optimize this, but this is basically how it works.

Colza

But which of the 2 ways of calculating autocorrelations is the better / correct one? – Cathartic

I consider the statsmodels way as the obvious one. For reference, this is also the way pointed out in Wikipedia. To check whether using the cross-correlation like pandas does is also a valid estimate, one would need to check the literature. FYI: Although this estimate by statsmodels is considered "unbiased" because we use n-k instead of n, it is still biased according to Wikipedia, because we use the sample mean and sample covariance for calculation. – Colza

I am a bit confused about the slicing method. Why should one use y1 = x[:(len(x)-lag)] y2 = x[lag:] instead of y1=x and y2=x.shift(lag)? (Source: geeksforgeeks.org/how-to-calculate-autocorrelation-in-python) In my case I've got the same result for both functions when using this slicing method. – Grenoble

Answer 2

In the following example, Pandas autocorr() function gives the expected results but statmodels acf() function does not.

Consider the following series:

import pandas as pd
s = pd.Series(range(10))

We expect that there is perfect correlation between this series and any of its lagged series, and this is actually what we get with autocorr() function

[ s.autocorr(lag=i) for i in range(10) ]
# [0.9999999999999999, 1.0, 1.0, 1.0, 1.0, 0.9999999999999999, 1.0, 1.0, 0.9999999999999999, nan]

But using acf() we get a different result:

from statsmodels.tsa.stattools import acf
acf(s)
# [ 1.          0.7         0.41212121  0.14848485 -0.07878788 
#  -0.25757576 -0.37575758 -0.42121212 -0.38181818 -0.24545455]

If we try acf with adjusted=True the result is even more unexpected because for some lags the result is less than -1 (note that correlation has to be in [-1, 1])

acf(s, adjusted=True)  # 'unbiased' is deprecated and 'adjusted' should be used instead
# [ 1.          0.77777778  0.51515152  0.21212121 -0.13131313 
#  -0.51515152 -0.93939394 -1.4040404  -1.90909091 -2.45454545]

Flame

Thanks for pointing this out. This would seem to be a problem for acf(). I wonder if the authors are aware of it. – Whip

Answer 3

As suggested in comments, the problem can be decreased, but not completely resolved, by supplying unbiased=True to the statsmodels function. Using a random input:

import statistics

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import acf

DATA_LEN = 100
N_TESTS = 100
N_LAGS = 32

def test(unbiased):
  data = pd.Series(np.random.random(DATA_LEN))
  data_acf_1 = acf(data, unbiased=unbiased, nlags=N_LAGS)
  data_acf_2 = [data.autocorr(i) for i in range(N_LAGS+1)]
  # return difference between results
  return sum(abs(data_acf_1 - data_acf_2))

for value in (False, True):
  diffs = [test(value) for _ in range(N_TESTS)]
  print(value, statistics.mean(diffs))

Output:

False 0.464562410987
True 0.0820847168593

Cuculiform