The question has tag Python, but using ctypes to call C++ code is also a Python feature. It contains 3 versions (I measure time cost of result = [ackermann(m,n) for m<=3, n <= 17], like in the top answer)
- Use int64_t and recursion with memoization => 32ms. It'll only work for small inputs (just like all the algorithms in the top answer). It's focused on optimizing recursive function.
- Use bignum and same algorithm as above => 32ms Since the bignum lib I used is implemented using 64 bit base type, if the result fit in small numbers it's no different from using
int64_t directly. I added this because comments mentioned it's unfair to compare C++ int64_t vs Python unlimited length integer.
- Use bignum + math formula => ~~0.14 ms This one will also work with bigger inputs.
Summary: > 3000x faster than top Python answer if you use math, or 13-15x faster if you don't use math. I use this single-header-file bignum library. Stackoverflow has answer length limit so I can't copy the file here.
// ackermann.cpp
#include <iostream>
#include <vector>
#include <chrono>
#include <string>
#include "num.hpp"
using namespace std;
class MyTimer {
std::chrono::time_point<std::chrono::system_clock> start;
public:
void startCounter() {
start = std::chrono::system_clock::now();
}
int64_t getCounterNs() {
return std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now() - start).count();
}
int64_t getCounterMs() {
return std::chrono::duration_cast<std::chrono::milliseconds>(std::chrono::system_clock::now() - start).count();
}
double getCounterMsPrecise() {
return std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now() - start).count()
/ 1000000.0;
}
};
extern "C" {
int64_t ackermann(int64_t m, int64_t n) {
static std::vector<int64_t> cache[4];
// special signal to clear cache
if (m < 0 && n < 0) {
for (int i = 0; i < 4; i++) {
cache[i].resize(0);
cache[i].shrink_to_fit();
}
return -1;
}
if (n >= cache[m].size()) {
int cur = cache[m].size();
cache[m].resize(n + 1);
for (int i = cur; i < n; i++) cache[m][i] = ackermann(m, i);
}
if (cache[m][n]) return cache[m][n];
if (m == 0) return cache[m][n] = n + 1;
// These 3 lines are kinda cheating, since it uses math formula for special case
// So I commented them out because the question is about optimizing recursion.
// if (m == 1) return cache[m][n] = n + 2;
// if (m == 2) return cache[m][n] = 2 * n + 3;
// if (m == 3) return cache[m][n] = (1LL << (n + 3)) - 3;
if (n == 0) return cache[m][n] = ackermann(m - 1, 1);
return cache[m][n] = ackermann(m - 1, ackermann(m, n - 1));
}
Num ackermann_bignum_smallres(int64_t m, int64_t n) {
static std::vector<Num> cache[4];
// special signal to clear cache
if (m < 0 && n < 0) {
for (int i = 0; i < 4; i++) {
cache[i].resize(0);
cache[i].shrink_to_fit();
}
return -1;
}
if (n >= cache[m].size()) {
int cur = cache[m].size();
cache[m].resize(n + 1);
for (int i = cur; i < n; i++) cache[m][i] = ackermann(m, i);
}
if (cache[m][n] > 0) return cache[m][n];
if (m == 0) return cache[m][n] = n + 1;
if (n == 0) return cache[m][n] = ackermann(m - 1, 1);
return cache[m][n] = ackermann(m - 1, ackermann(m, n - 1));
}
//-----
Num bignum_pow(const Num& x, const Num& n) {
if (n == 0) return 1;
Num mid = bignum_pow(x, n / 2);
if (n % 2 == 0) return mid * mid;
else return mid * mid * x;
}
Num ackermann_bignum(Num m, Num n) {
if (m <= 1) return n + (m + 1);
else if (m == 2) return Num(2) * n + 3;
else if (m == 3) return bignum_pow(2, n + 3) - 3;
else {
cout << "Don't put m >= 4\n";
exit(1);
}
}
}
Num dummy = 0;
int main(int argc, char* argv[])
{
int test_type = 0;
if (argc > 1) {
try {
test_type = std::stoi(string(argv[1]));
} catch (...) {
test_type = 0;
}
}
int lim = (test_type == 0) ? 63 : 17;
MyTimer timer;
timer.startCounter();
for (int m = 0; m <= 3; m++)
for (int n = 0; n <= lim; n++) {
if (test_type == 0) {
dummy = ackermann_bignum(m, n);
} else if (test_type == 1) {
dummy = ackermann_bignum_smallres(m, n);
} else {
dummy = ackermann(m, n);
}
cout << "ackermann(" << m << ", " << n << ") = " << dummy << "\n";
}
cout << "ackermann cost = " << timer.getCounterMsPrecise() << "\n";
}
Compile the above using g++ ackermann.cpp -shared -fPIC -O3 -std=c++17 -o ackermann.so
To run separately, use
g++ -o main_cpp ackermann.cpp -O3 -std=c++17
./main_cpp
Then in the same folder, run this script (modified from @Stefan Pochmann answer)
def A_Stefan_row_class(m, n):
class A0:
def __getitem__(self, n):
return n + 1
class A:
def __init__(self, a):
self.a = a
self.n = 0
self.value = a[1]
def __getitem__(self, n):
while self.n < n:
self.value = self.a[self.value]
self.n += 1
return self.value
a = A0()
for _ in range(m):
a = A(a)
return a[n]
from collections import defaultdict
def A_Stefan_row_lists(m, n):
memo = defaultdict(list)
def a(m, n):
if not m:
return n + 1
if m not in memo:
memo[m] = [a(m-1, 1)]
Am = memo[m]
while len(Am) <= n:
Am.append(a(m-1, Am[-1]))
return Am[n]
return a(m, n)
from itertools import count
def A_Stefan_generators(m, n):
a = count(1)
def up(a, x=1):
for i, ai in enumerate(a):
if i == x:
x = ai
yield x
for _ in range(m):
a = up(a)
return next(up(a, n))
def A_Stefan_paper(m, n):
next = [0] * (m + 1)
goal = [1] * m + [-1]
while True:
value = next[0] + 1
transferring = True
i = 0
while transferring:
if next[i] == goal[i]:
goal[i] = value
else:
transferring = False
next[i] += 1
i += 1
if next[m] == n + 1:
return value
def A_Stefan_generators_2(m, n):
def a0():
n = yield
while True:
n = yield n + 1
def up(a):
next(a)
a = a.send
i, x = -1, 1
n = yield
while True:
while i < n:
x = a(x)
i += 1
n = yield x
a = a0()
for _ in range(m):
a = up(a)
next(a)
return a.send(n)
def A_Stefan_m_recursion(m, n):
ix = [None] + [(-1, 1)] * m
def a(m, n):
if not m:
return n + 1
i, x = ix[m]
while i < n:
x = a(m-1, x)
i += 1
ix[m] = i, x
return x
return a(m, n)
def A_Stefan_function_stack(m, n):
def a(n):
return n + 1
for _ in range(m):
def a(n, a=a, ix=[-1, 1]):
i, x = ix
while i < n:
x = a(x)
i += 1
ix[:] = i, x
return x
return a(n)
from itertools import count, islice
def A_Stefan_generator_stack(m, n):
a = count(1)
for _ in range(m):
a = (
x
for a, x in [(a, 1)]
for i, ai in enumerate(a)
if i == x
for x in [ai]
)
return next(islice(a, n, None))
from itertools import count, islice
def A_Stefan_generator_stack2(m, n):
a = count(1)
def up(a):
i, x = 0, 1
while True:
i, x = x+1, next(islice(a, x-i, None))
yield x
for _ in range(m):
a = up(a)
return next(islice(a, n, None))
def A_Stefan_generator_stack3(m, n):
def a(m):
if not m:
yield from count(1)
x = 1
for i, ai in enumerate(a(m-1)):
if i == x:
x = ai
yield x
return next(islice(a(m), n, None))
def A_Stefan_generator_stack4(m, n):
def a(m):
if not m:
return count(1)
return (
x
for x in [1]
for i, ai in enumerate(a(m-1))
if i == x
for x in [ai]
)
return next(islice(a(m), n, None))
def A_templatetypedef(i, n):
positions = [-1] * (i + 1)
values = [0] + [1] * i
while positions[i] != n:
values[0] += 1
positions[0] += 1
j = 1
while j <= i and positions[j - 1] == values[j]:
values[j] = values[j - 1]
positions[j] += 1
j += 1
return values[i]
import ctypes
mylib = ctypes.CDLL('./ackermann.so')
mylib.ackermann.argtypes = [ctypes.c_int64, ctypes.c_int64]
mylib.ackermann.restype = ctypes.c_int64
def c_ackermann(m, n):
return mylib.ackermann(m,n)
funcs = [
c_ackermann,
A_Stefan_row_class,
A_Stefan_row_lists,
A_Stefan_generators,
A_Stefan_paper,
A_Stefan_generators_2,
A_Stefan_m_recursion,
A_Stefan_function_stack,
A_Stefan_generator_stack,
A_Stefan_generator_stack2,
A_Stefan_generator_stack3,
A_Stefan_generator_stack4,
A_templatetypedef
]
N = 18
args = (
[(0, n) for n in range(N)] +
[(1, n) for n in range(N)] +
[(2, n) for n in range(N)] +
[(3, n) for n in range(N)]
)
from time import time
def print(*args, print=print, file=open('out.txt', 'w')):
print(*args)
print(*args, file=file, flush=True)
expect = none = object()
for _ in range(3):
for f in funcs:
t = time()
result = [f(m, n) for m, n in args]
# print(f'{(time()-t) * 1e3 :5.1f} ms ', f.__name__)
print(f'{(time()-t) * 1e3 :5.0f} ms ', f.__name__)
if expect is none:
expect = result
elif result != expect:
raise Exception(f'{f.__name__} failed')
del result
print()
c_ackermann(-1, -1)
Output:
32 ms c_ackermann
1897 ms A_Stefan_row_class
1427 ms A_Stefan_row_lists
437 ms A_Stefan_generators
1366 ms A_Stefan_paper
479 ms A_Stefan_generators_2
801 ms A_Stefan_m_recursion
725 ms A_Stefan_function_stack
716 ms A_Stefan_generator_stack
1113 ms A_Stefan_generator_stack2
551 ms A_Stefan_generator_stack3
682 ms A_Stefan_generator_stack4
1622 ms A_templatetypedef

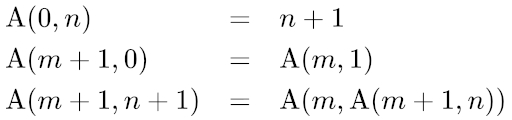
print(m, n)a the beginning and callA(3, 2). You will see repeated values over and over. E.g. A(1, 5) is called 16 times. Caching will most definitely make it faster. – Plimsoll