Linear Regression :: Normalization (Vs) Standardization

Question

I am using Linear regression to predict data. But, I am getting totally contrasting results when I Normalize (Vs) Standardize variables.

Normalization = x -xmin/ xmax – xmin   Zero Score Standardization = x - xmean/ xstd  

a) Also, when to Normalize (Vs) Standardize ?
b) How Normalization affects Linear Regression?
c) Is it okay if I don't normalize all the attributes/lables in the linear regression?

Thanks, Santosh

Tushy

This question was helpful - to bring out the basics of these important data characteristics. – Popgun

stats.stackexchange.com/q/10289/173093 this question may also help – Wells

Answer 1

Note that the results might not necessarily be so different. You might simply need different hyperparameters for the two options to give similar results.

The ideal thing is to test what works best for your problem. If you can't afford this for some reason, most algorithms will probably benefit from standardization more so than from normalization.

See here for some examples of when one should be preferred over the other:

For example, in clustering analyses, standardization may be especially crucial in order to compare similarities between features based on certain distance measures. Another prominent example is the Principal Component Analysis, where we usually prefer standardization over Min-Max scaling, since we are interested in the components that maximize the variance (depending on the question and if the PCA computes the components via the correlation matrix instead of the covariance matrix; but more about PCA in my previous article).

However, this doesn’t mean that Min-Max scaling is not useful at all! A popular application is image processing, where pixel intensities have to be normalized to fit within a certain range (i.e., 0 to 255 for the RGB color range). Also, typical neural network algorithm require data that on a 0-1 scale.

One disadvantage of normalization over standardization is that it loses some information in the data, especially about outliers.

Also on the linked page, there is this picture:

As you can see, scaling clusters all the data very close together, which may not be what you want. It might cause algorithms such as gradient descent to take longer to converge to the same solution they would on a standardized data set, or it might even make it impossible.

"Normalizing variables" doesn't really make sense. The correct terminology is "normalizing / scaling the features". If you're going to normalize or scale one feature, you should do the same for the rest.

Dieball

Thanks. From your explanation it appears to me that always we should "standardize variables". Also can you please elaborate on this : "If you're going to normalize or scale one feature, you should do the same for the rest.". Also, in my dataset I have attributes such as long, latitude, altitude do we need to normalize them also. – Tushy

I have a different point of view of the things. Most of the time, centering the data is good. But scaling is something else. Because sometimes different feature needs different scaling (For example, if always the data has to be with 1 STD why would something like Mahalanobis Distance exist?). This is scaling and it should taken in place just if this is what you need. – Johnathon

@SantoshKumar I mean that the answer to c) is no in general. It's generally not ok if you don't normalize all the attributes. I don't know the specifics of your particular problem, things might be different for it, but it's unlikely. So yes, you should most likely normalize or scale those as well. – Dieball

@Drazick that's not such a different point of view I think. Most machine learning algorithms don't use something like the Mahalanobis distance, so that's not very relevant. Standardization is generally the right thing, but there can be exceptions. It's just that, if you're not sure and can't afford to test, chances are you'll be just fine by standardizing. – Dieball

I think on the contrary, on most cases you should tell the algorithm the real geometry of the data using the Covariance Matrix instead normalizing it. For Optimization Algorithm, well, that a different story. – Johnathon

@Drazick but what machine learning algorithms accept a covariance matrix? Certainly not most of them. – Dieball

K-Means, Least Squares, Any other algorithm which is based on the euclidean distance between vectors and assume the distance id euclidean while in most cases it doesn't. – Johnathon

@Drazick I upvoted this but would also like Drazick to contribute an answer to understand his points more carefully. – Popgun

@javadba, I will try to create something to illustrate my ideas. Basically, I would divide it into 3 things: 1. Centering (required mostly in LS when no DC component is given or before PCA like analysis), 2. Normalization - Makes sense mostly when using Gradient dependent optimization algorithms. As it sometimes helps the convergence. 3. Do Nothing - Mostly when the location and and the STD of the features is part of what you try to infer (Think how many times you try to infer something which Covariance Matrix related).. – Johnathon

Answer 2

That makes sense because normalization and standardization do different things.

Normalization transforms your data into a range between 0 and 1

Standardization transforms your data such that the resulting distribution has a mean of 0 and a standard deviation of 1

Normalization/standardization are designed to achieve a similar goal, which is to create features that have similar ranges to each other. We want that so we can be sure we are capturing the true information in a feature, and that we dont over weigh a particular feature just because its values are much larger than other features.

If all of your features are within a similar range of each other then theres no real need to standardize/normalize. If, however, some features naturally take on values that are much larger/smaller than others then normalization/standardization is called for

If you're going to be normalizing at least one variable/feature, I would do the same thing to all of the others as well

Pyrography

That's not really true. The ranges of features is one part of the problem, but a lot of algorithms benefit from the standardization part. Simple scaling can lose important information in the data, especially relating to outliers. RBF kernels work much worse on unstandardized data. The goals aren't the same. – Dieball

Thanks. c) Is it okay if I don't normalize all the attributes/lables in the linear regression? – Tushy

Answer 3

First question is why we need Normalisation/Standardisation?

=> We take a example of dataset where we have salary variable and age variable. Age can take range from 0 to 90 where salary can be from 25,000 to 250,000.

We compare difference for 2 person then age difference will be in range of below 100 where salary difference will in range of thousands.

So if we don't want one variable to dominate other then we use either Normalisation or Standardization. Now both age and salary will be in same scale but when we use standardiztion or normalisation, we lose original values and it is transformed to some values. So loss of interpretation but extremely important when we want to draw inference from our data.

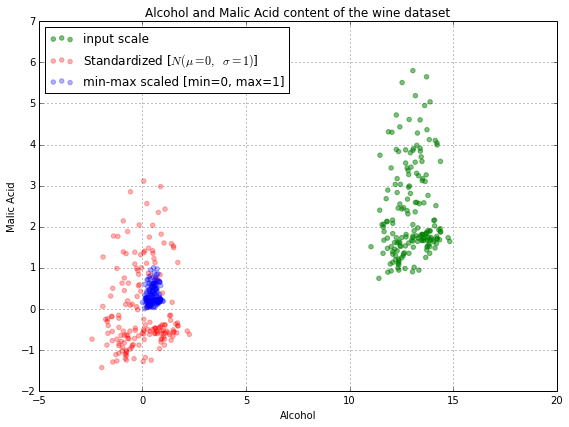
Normalization rescales the values into a range of [0,1]. also called min-max scaled.

Standardization rescales data to have a mean (μ) of 0 and standard deviation (σ) of 1.So it gives a normal graph.

Example below:

Another example:

In above image, you can see that our actual data(in green) is spread b/w 1 to 6, standardised data(in red) is spread around -1 to 3 whereas normalised data(in blue) is spread around 0 to 1.

Normally many algorithm required you to first standardise/normalise data before passing as parameter. Like in PCA, where we do dimension reduction by plotting our 3D data into 1D(say).Here we required standardisation.

But in Image processing, it is required to normalise pixels before processing. But during normalisation, we lose outliers(extreme datapoints-either too low or too high) which is slight disadvantage.

So it depends on our preference what we chose but standardisation is most recommended as it gives a normal curve.

Cameleer

Answer 4

None of the mentioned transformations shall matter for linear regression as these are all affine transformations.

Found coefficients would change but explained variance will ultimately remain the same. So, from linear regression perspective, Outliers remain as outliers (leverage points).

And these transformations also will not change the distribution. Shape of the distribution remains the same.

Isobath

Answer 5

lot of people use Normalisation and Standardisation interchangeably. The purpose remains the same is to bring features into the same scale. The approach is to subtract each value from min value or mean and divide by max value minus min value or SD respectively. The difference you can observe that when using min value u will get all value + ve and mean value u will get bot + ve and -ve values. This is also one of the factors to decide which approach to use.

Tatiana