MinAreaRect angles - Unsure about the angle returned

Question

From the functions for MinAreaRect, does it return angles in the range of 0-360 degrees? I am unsure as i have an object that is oriented at 90 degrees or so but I keep getting either -1 or -15 degrees. Could this be an openCV error?

Any guidance much appreciated.

Thanks

Proteus

Answer 1

I'm going to assume you're using C++, but the answer should be the same if you're using C or Python.

The function minAreaRect seems to give angles ranging from -90 to 0 degrees, not including zero, so an interval of [-90, 0).

The function gives -90 degrees if the rectangle it outputs isn't rotated, i.e. the rectangle has two sides exactly horizontal and two sides exactly vertical. As the rectangle rotates clockwise, the angle increases (goes towards zero). When zero is reached, the angle given by the function ticks back over to -90 degrees again.

So if you have a long rectangle from minAreaRect, and it's lying down flat, minAreaRect will call the angle -90 degrees. If you rotate the image until the rectangle given by minAreaRect is perfectly upright, then the angle will say -90 degrees again.

I didn't actually know any of this (I procrastinated from my OpenCV project to find out how it works :/). Anyway, here's an OpenCV program that demonstrates minAreaRect if I haven't explained it clear enough already:

#include <stdio.h>

#include <opencv\cv.h>
#include <opencv\highgui.h>

using namespace cv;

int main() {
    float angle = 0;
    Mat image(200, 400, CV_8UC3, Scalar(0));
    RotatedRect originalRect;
    Point2f vertices[4];
    vector<Point2f> vertVect;
    RotatedRect calculatedRect;

    while (waitKey(5000) != 27) {
        // Create a rectangle, rotating it by 10 degrees more each time.
        originalRect = RotatedRect(Point2f(100,100), Size2f(100,50), angle);

        // Convert the rectangle to a vector of points for minAreaRect to use.
        // Also move the points to the right, so that the two rectangles aren't
        // in the same place.
        originalRect.points(vertices);
        for (int i = 0; i < 4; i++) {
            vertVect.push_back(vertices[i] + Point2f(200, 0));
        }

        // Get minAreaRect to find a rectangle that encloses the points. This
        // should have the exact same orientation as our original rectangle.
        calculatedRect = minAreaRect(vertVect);

        // Draw the original rectangle, and the one given by minAreaRect.
        for (int i = 0; i < 4; i++) {
            line(image, vertices[i], vertices[(i+1)%4], Scalar(0, 255, 0));
            line(image, vertVect[i], vertVect[(i+1)%4], Scalar(255, 0, 0));
        }
        imshow("rectangles", image);

        // Print the angle values.
        printf("---\n");
        printf("Original angle:             %7.2f\n", angle);
        printf("Angle given by minAreaRect: %7.2f\n", calculatedRect.angle);
        printf("---\n");

        // Reset everything for the next frame.
        image = Mat(200, 400, CV_8UC3, Scalar(0));
        vertVect.clear();
        angle+=10;
    }

    return 0;
}

This lets you easily see how the angle, and shape, of a manually drawn rectangle compares to the minAreaRect interpretation of the same rectangle.

Partner

Dude you are a serious gem. Thanks :) – Proteus

No problem :) OpenCV's documentation seems to miss a lot of important details – Partner

Just one more question, how can I get a 0-360 degree transformation from rotatedrect if it only gives angels between between -90,-1 ? And yes opencv is possibly better on documentation when you dig into code or their samples – Proteus

Well, there's no way that OpenCV can work that out on its own. It's hard to say without knowing exactly what you're doing, but the approach I'd take is to get a feature point on your object which is towards one side. Then, when you get the rectangle from minAreaRect, you can see where in the rectangle the point is and use that to work out the orientation of your object. – Partner

Ok thanks, may be I will have to look into and do as you said – Proteus

Well actually I did it. I have a hand bounded by the MinAreaRect, all I needed to to was to pick the vertices and find out the angles using arc tangent. Nevertheless, this solves me a big headache. Thumbs up :) – Proteus

Answer 2

Improving on the answer of @Adam Goodwin i want to add my little code that changes the behaviour a little bit:

I wanted to have the angle between the longer side and vertical (to me it is the most natural way to think about rotated rectangles):

If you need the same, just use this code:

void printAngle(RotatedRect calculatedRect){
    if(calculatedRect.size.width < calculatedRect.size.height){
        printf("Angle along longer side: %7.2f\n", calculatedRect.angle+180);
    }else{
        printf("Angle along longer side: %7.2f\n", calculatedRect.angle+90);
    }
}

To see it in action just insert it in Adam Goodwins code:

printf("Angle given by minAreaRect: %7.2f\n", calculatedRect.angle);
printAngle(calculatedRect);
printf("---\n");

Zoltai

if i want to check my rotatedrect.angle in 360degrees. How can we do it. since your current code will work with 0-180 degrees with vertical. Any hint? – Portingale

Answer 3

After experiment, I find that if the long side is in the left of the bottom Point, the angle value is between long side and Y+ axis, but if the long side is in the right of the bottom Point, the angle value is between long side and X+ axis. So I use the code like this(java):

       rRect = Imgproc.minAreaRect(mop2f);
       if(rRect.size.width<rRect.size.height){
            angle = 90 -rRect.angle;
        }else{
            angle = -rRect.angle;
        }

The angle is from 0 to 180.

Sheilasheilah

Answer 4

After much experiment, I have found that the relationship between the rectangle orientation and output angle of minAreaRect(). It can be summarized in the following image

The following description assume that we have a rectangle with unequal height and width length, i.e., it is not square.

If the rectangle lies vertically (width < height), then the detected angle is -90. If the rectangle lies horizontally, then the detected angle is also -90 degree.

If the top part of the rectangle is in first quadrant, then the detected angle decreases as the rectangle rotate from horizontal to vertical position, until the detected angle becomes -90 degrees. In first quadrant, the width of detected rectangle is longer than its height.

If the top part of the detected rectangle is in second quadrant, then the angle decreases as the rectangle rotate from vertical to horizontal position. But there is a difference between second and first quadrant. If the rectangle approaches vertical position but has not been in vertical position, its angle approaches 0. If the rectangle approaches horizontal position but has not been in horizontal position, its angle approaches -90 degrees.

This post here is also good in explaining this.

Magdaleno

Answer 5

It depends on the version of opencv, at least for Python.

For opencv-python='4.5.4.60'. The angle is that between positive x-axis and the first line the axis meets when it rotates anti-clock wise. The following is the code to snippet.

import cv2
import numpy as np

box1 = [[0, 0], [1, 0], [1, 2], [0, 2]]
cv2.minAreaRect(np.asarray(box1))  # angel = 90.0

box2 = [[0, 0], [2, 0], [2, 1], [0, 1]]
cv2.minAreaRect(np.asarray(box2))  # angel = 90.0

box3 = [[0, 0], [2**0.5, 2**0.5], [0.5*2**0.5, 1.5*2**0.5], [-0.5*2**0.5, 0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box3, dtype=np.float32))  # angle = 44.999

box4 = [[0, 0], [-2**0.5, 2**0.5], [-0.5*2**0.5, 1.5*2**0.5], [0.5*2**0.5, 0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box4, dtype=np.float32))  # angle = 45.0

box5 = [[0, 0], [-0.5*2**0.5, 0.5*2**0.5], [-2**0.5, 0], [-0.5*2**0.5, -0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box5, dtype=np.float32))  # angle = 45.0

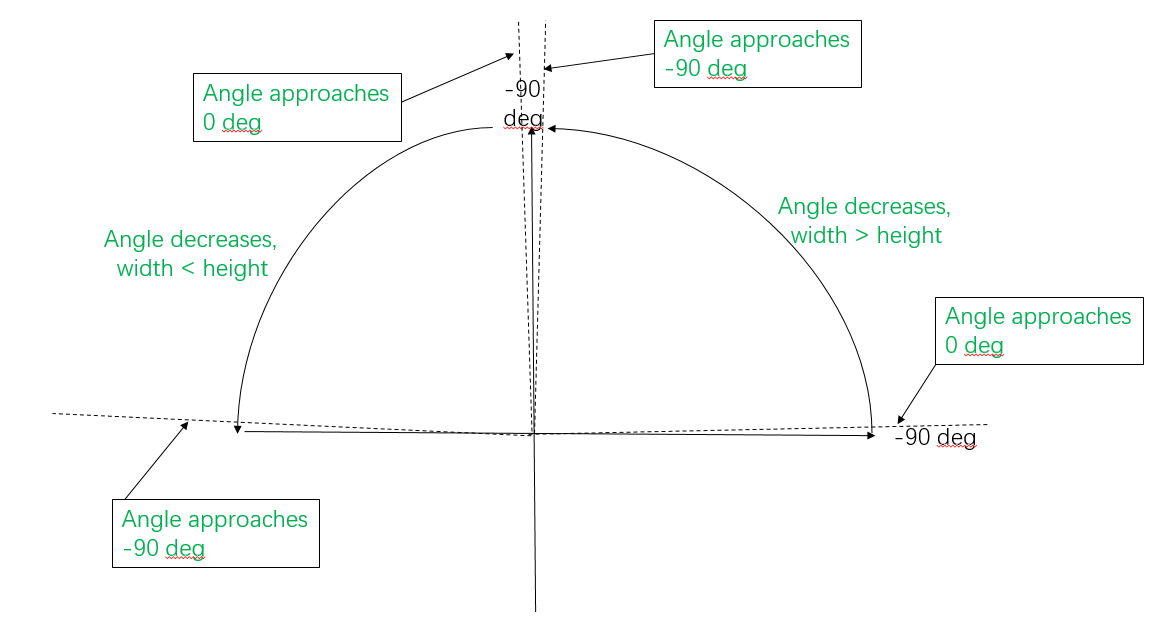
For opencv-python='3.4.13.47'. The angle is that between positive x-axis and the first line the axis meets when it rotates clock wise. The following is the code to snippet.

import cv2
import numpy as np

box1 = [[0, 0], [1, 0], [1, 2], [0, 2]]
cv2.minAreaRect(np.asarray(box1))  # angel = -90.0

box2 = [[0, 0], [2, 0], [2, 1], [0, 1]]
cv2.minAreaRect(np.asarray(box2))  # angel = -90.0

box3 = [[0, 0], [2**0.5, 2**0.5], [0.5*2**0.5, 1.5*2**0.5], [-0.5*2**0.5, 0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box3, dtype=np.float32))  # angle = -44.999

box4 = [[0, 0], [-2**0.5, 2**0.5], [-0.5*2**0.5, 1.5*2**0.5], [0.5*2**0.5, 0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box4, dtype=np.float32))  # angle = -45.0

box5 = [[0, 0], [-0.5*2**0.5, 0.5*2**0.5], [-2**0.5, 0], [-0.5*2**0.5, -0.5*2**0.5]]
cv2.minAreaRect(np.asarray(box5, dtype=np.float32))  # angle = -45.0

Cavanaugh