How do I run a high pass or low pass filter on data points in R?

Question

I am a beginner in R and I have tried to find information about the following without finding anything.

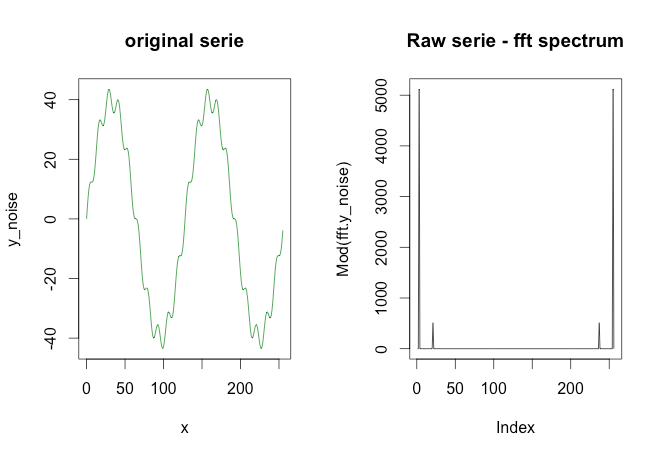
The green graph in the picture is composed by the red and yellow graphs. But let's say that I only have the data points of something like the green graph. How do I extract the low/high frequencies (i.e. approximately the red/yellow graphs) using a low pass/high pass filter?

Update: The graph was generated with

number_of_cycles = 2
max_y = 40

x = 1:500
a = number_of_cycles * 2*pi/length(x)

y = max_y * sin(x*a)
noise1 = max_y * 1/10 * sin(x*a*10)

plot(x, y, type="l", col="red", ylim=range(-1.5*max_y,1.5*max_y,5))
points(x, y + noise1, col="green", pch=20)
points(x, noise1, col="yellow", pch=20)

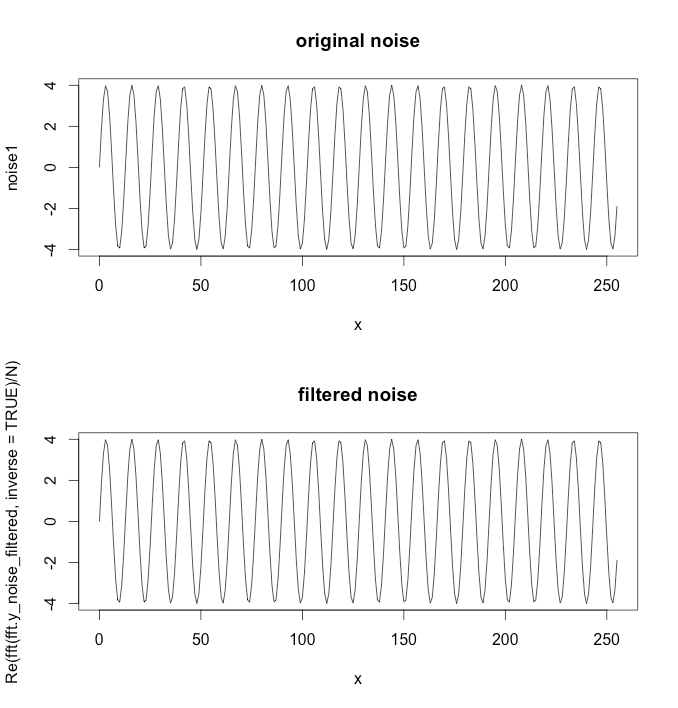
Update 2: Using the Butterworth filter in the signal package suggested I get the following:

library(signal)

bf <- butter(2, 1/50, type="low")
b <- filter(bf, y+noise1)
points(x, b, col="black", pch=20)

bf <- butter(2, 1/25, type="high")
b <- filter(bf, y+noise1)
points(x, b, col="black", pch=20)

The calculations was a bit work, signal.pdf gave next to no hints about what values W should have, but the original octave documentation at least mentioned radians which got me going. The values in my original graph was not chosen with any specific frequency in mind, so I ended up with the following not so simple frequencies: f_low = 1/500 * 2 = 1/250, f_high = 1/500 * 2*10 = 1/25 and the sampling frequency f_s = 500/500 = 1. Then I chose a f_c somewhere inbetween the low and high frequencies for the low/high pass filters (1/100 and 1/50 respectively).

Use

If you give us a reproducible example, eg the data / code you used for the graph, people will be able to help you more easily. It would help to show us what you tried until now. – Leprose

To add : the signal package contains all kind of filters for this : cran.r-project.org/web/packages/signal/signal.pdf – Leprose

this is in any case a far too broad programming question. You should at least specify which filter you want to use. There is a whole number of options which may or may not make sense on your real data. – Leprose

@Joris Please make your comment about signals into an answer, and I'll accpet that. It was what I was looking for (though I find that I have to do a massive relearning of what I learned about filters years ago...). – Use

Came up in this answer on Cross Validated, FYI! – Ranjiv

Very nice follow up and editing for the question. I found the answers in your edits useful. +1 – Flue

I think you have missed the entire field of Fourier analysis. A properly applied analysis should have been able to extract the fact that there were two only sinusoidal signals. – Hogarth

Answer 1

Per request of OP:

The signal package contains all kinds of filters for signal processing. Most of it is comparable to / compatible with the signal processing functions in Matlab/Octave.

Leprose

Answer 2

I bumped into similar problem recently and did not find the answers here particularly helpful. Here is an alternative approach.

Let´s start by defining the example data from the question:

number_of_cycles = 2
max_y = 40

x = 1:500
a = number_of_cycles * 2*pi/length(x)

y = max_y * sin(x*a)
noise1 = max_y * 1/10 * sin(x*a*10)
y <- y + noise1

plot(x, y, type="l", ylim=range(-1.5*max_y,1.5*max_y,5), lwd = 5, col = "green")

So the green line is the dataset we want to low-pass and high-pass filter.

Side note: The line in this case could be expressed as a function by using cubic spline (spline(x,y, n = length(x))), but with real world data this would rarely be the case, so let's assume that it is not possible to express the dataset as a function.

The easiest way to smooth such data I have came across is to use loess or smooth.spline with appropriate span/spar. According to statisticians loess/smooth.spline is probably not the right approach here, as it does not really present a defined model of the data in that sense. An alternative is to use Generalized Additive Models (gam() function from package mgcv). My argument for using loess or smoothed spline here is that it is easier and does not make a difference as we are interested in the visible resulting pattern. Real world datasets are more complicated than in this example and finding a defined function for filtering several similar datasets might be difficult. If the visible fit is good, why to make it more complicated with R2 and p values? To me the application is visual for which loess/smoothed splines are appropriate methods. Both of the methods assume polynomial relationships with the difference that loess is more flexible also using higher degree polynomials, while cubic spline is always cubic (x^2). Which one to use depends on trends in a dataset. That said, the next step is to apply a low-pass filter on the dataset by using loess() or smooth.spline():

lowpass.spline <- smooth.spline(x,y, spar = 0.6) ## Control spar for amount of smoothing
lowpass.loess <- loess(y ~ x, data = data.frame(x = x, y = y), span = 0.3) ## control span to define the amount of smoothing

lines(predict(lowpass.spline, x), col = "red", lwd = 2)
lines(predict(lowpass.loess, x), col = "blue", lwd = 2)

Red line is the smoothed spline filter and blue the loess filter. As you see results differ slightly. I guess one argument of using GAM would be to find the best fit, if the trends really were this clear and consistent among datasets, but for this application both of these fits are good enough for me.

After finding a fitting low-pass filter, the high-pass filtering is as simple as subtracting the low-pass filtered values from y:

highpass <- y - predict(lowpass.loess, x)
lines(x, highpass, lwd =  2)

This answer comes late, but I hope it helps someone else struggling with similar problem.

Flue

Thank you, excellent answer. I'll remember this for next time I'll run into this kind of problem. – Use

Answer 3

Use filtfilt function instead of filter (package signal) to get rid of signal shift.

library(signal)
bf <- butter(2, 1/50, type="low")
b1 <- filtfilt(bf, y+noise1)
points(x, b1, col="red", pch=20)

Maganmagana

Just use this function carefully, as in its documentations there is "... so this function needs some work yet - and is in the state of the year 2000 version of the Octave code." – Remus

Answer 4

One method is using the fast fourier transform implemented in R as fft. Here is an example of a high pass filter. From the plots above, the idea implemented in this example is to get the serie in yellow starting from the serie in green (your real data).

# I've changed the data a bit so it's easier to see in the plots
par(mfrow = c(1, 1))
number_of_cycles = 2
max_y = 40
N <- 256

x = 0:(N-1)
a = number_of_cycles * 2 * pi/length(x)

y = max_y * sin(x*a)
noise1 = max_y * 1/10 * sin(x*a*10)
plot(x, y, type="l", col="red", ylim=range(-1.5*max_y,1.5*max_y,5))
points(x, y + noise1, col="green", pch=20)
points(x, noise1, col="yellow", pch=20)

### Apply the fft to the noisy data
y_noise = y + noise1
fft.y_noise = fft(y_noise)


# Plot the series and spectrum
par(mfrow = c(1, 2))
plot(x, y_noise, type='l', main='original serie', col='green4')
plot(Mod(fft.y_noise), type='l', main='Raw serie - fft spectrum')

### The following code removes the first spike in the spectrum
### This would be the high pass filter
inx_filter = 15
FDfilter = rep(1, N)
FDfilter[1:inx_filter] = 0
FDfilter[(N-inx_filter):N] = 0
fft.y_noise_filtered = FDfilter * fft.y_noise

par(mfrow = c(2, 1))
plot(x, noise1, type='l', main='original noise')
plot(x, y=Re( fft( fft.y_noise_filtered, inverse=TRUE) / N ) , type='l', 
     main = 'filtered noise')

Appellant

Answer 5

Check out this link where there's R code for filtering (medical signals). It's by Matt Shotwell and the site is full of interesting R/stats info with a medical bent:

biostattmat.com

The package fftfilt contains lots of filtering algorithms that should help too.

Controversy

there's a package for that. Copying a manual implementation of a very basic filter from which you don't know whether it would actually perform, is not a good idea. – Leprose

Answer 6

I also struggled to figure out how the W parameter in the butter function maps on to the filter cut-off, in part because the documentation for filter and filtfilt is incorrect as of posting (it suggests that W = .1 would result in a 10 Hz lp filter when combined with filtfilt when signal sampling rate Fs = 100, but actually, it's only a 5 Hz lp filter -- the half-amplitude cut-off is 5 Hz when use filtfilt, but the half-power cut-off is 5 Hz when you only apply the filter once, using the filter function). I'm posting some demo code I wrote below that helped me confirm how this is all working, and that you could use to check a filter is doing what you want.

#Example usage of butter, filter, and filtfilt functions
#adapted from https://rdrr.io/cran/signal/man/filtfilt.html

library(signal)

Fs <- 100; #sampling rate

bf <- butter(3, 0.1);       
#when apply twice with filtfilt, 
#results in a 0 phase shift 
#5 Hz half-amplitude cut-off LP filter
#
#W * (Fs/2) == half-amplitude cut-off when combined with filtfilt
#
#when apply only one time, using the filter function (non-zero phase shift),
#W * (Fs/2) == half-power cut-off


t <- seq(0, .99, len = 100)   # 1 second sample

#generate a 5 Hz sine wave
x <- sin(2*pi*t*5)

#filter it with filtfilt
y <- filtfilt(bf, x)

#filter it with filter
z <- filter(bf, x)

#plot original and filtered signals
plot(t, x, type='l')
lines(t, y, col="red")
lines(t,z,col="blue")

#estimate signal attenuation (proportional reduction in signal amplitude)
1 - mean(abs(range(y[t > .2 & t < .8]))) #~50% attenuation at 5 Hz using filtfilt

1 - mean(abs(range(z[t > .2 & t < .8]))) #~30% attenuation at 5 Hz using filter

#demonstration that half-amplitude cut-off is 6 Hz when apply filter only once
x6hz <- sin(2*pi*t*6)

z6hz <- filter(bf, x6hz)

1 - mean(abs(range(z6hz[t > .2 & t < .8]))) #~50% attenuation at 6 Hz using filter


#plot the filter attenuation profile (for when apply one time, as with "filter" function):

hf <- freqz(bf, Fs = Fs);

plot(c(0, 20, 20, 0, 0), c(0, 0, 1, 1, 0), type = "l", 
 xlab = "Frequency (Hz)", ylab = "Attenuation (abs)")

lines(hf$f[hf$f<=20], abs(hf$h)[hf$f<=20])

plot(c(0, 20, 20, 0, 0), c(0, 0, -50, -50, 0),
 type = "l", xlab = "Frequency (Hz)", ylab = "Attenuation (dB)")

lines(hf$f[hf$f<=20], 20*log10(abs(hf$h))[hf$f<=20])

hf$f[which(abs(hf$h) - .5 < .001)[1]] #half-amplitude cutoff, around 6 Hz

hf$f[which(20*log10(abs(hf$h))+6 < .2)[1]] #half-amplitude cutoff, around 6 Hz

hf$f[which(20*log10(abs(hf$h))+3 < .2)[1]] #half-power cutoff, around 5 Hz

Atween

Answer 7

there is a package on CRAN named FastICA, this computes the approximation of the independent source signals, however in order to compute both signals you need a matrix of at least 2xn mixed observations (for this example), this algorithm can't determine the two indpendent signals with just 1xn vector. See the example below. hope this can help you.

number_of_cycles = 2
max_y = 40

x = 1:500
a = number_of_cycles * 2*pi/length(x)

y = max_y * sin(x*a)
noise1 = max_y * 1/10 * sin(x*a*10)

plot(x, y, type="l", col="red", ylim=range(-1.5*max_y,1.5*max_y,5))
points(x, y + noise1, col="green", pch=20)
points(x, noise1, col="yellow", pch=20)
######################################################
library(fastICA)
S <- cbind(y,noise1)#Assuming that "y" source1 and "noise1" is source2
A <- matrix(c(0.291, 0.6557, -0.5439, 0.5572), 2, 2) #This is a mixing matrix
X <- S %*% A 

a <- fastICA(X, 2, alg.typ = "parallel", fun = "logcosh", alpha = 1,
method = "R", row.norm = FALSE, maxit = 200,
tol = 0.0001, verbose = TRUE)

par(mfcol = c(2, 3))
plot(S[,1 ], type = "l", main = "Original Signals",
xlab = "", ylab = "")
plot(S[,2 ], type = "l", xlab = "", ylab = "")
plot(X[,1 ], type = "l", main = "Mixed Signals",
xlab = "", ylab = "")
plot(X[,2 ], type = "l", xlab = "", ylab = "")
plot(a$S[,1 ], type = "l", main = "ICA source estimates",
xlab = "", ylab = "")
plot(a$S[, 2], type = "l", xlab = "", ylab = "")

Rajah

Answer 8

I am not sure if any filter is the best way for You. More useful instrument for that aim is the fast Fourier transformation.

Eslinger