How to find leap year programmatically in C

Question

I wrote a program in C to find whether the entered year is a leap year or not. But unfortunately its not working well. It says a year is leap and the preceding year is not leap.

#include <stdio.h>
#include <conio.h>

int yearr(int year);

void main(void) {
    int year;
    printf("Enter a year:");
    scanf("%d", &year);
    if (!yearr(year)) {
        printf("It is a leap year.");
    } else {
        printf("It is not a leap year");
    }

    getch();
}

int yearr(int year) {
    if ((year % 4 == 0) && (year / 4 != 0))
        return 1;
    else
        return 0;
}

After reading the comments I edited my code as:

#include <stdio.h>
#include <conio.h>

int yearr(int year);

void main(void) {
    int year;
    printf("Enter a year:");
    scanf("%d", &year);
    if (!yearr(year)) {
        printf("It is a leap year.");
    } else {
        printf("It is not a leap year");
    }

    getch();
}

int yearr(int year) {
    if (year % 4 == 0) {
        if (year % 400 == 0)
            return 1;
        if (year % 100 == 0)
            return 0; 
    } else
        return 0;
}

Lubricity

Did it work? Also, code readability is important, so yearr is a poor name for a function to find if a year is a leap year. main returns int in C, not void. – Mirage

When compiling the revised code, GCC says: In function ‘yearr’: yearr.c:12: warning: control reaches end of non-void function. If you indent your code properly, you'll find it easier to see why that's the case -- suffice to say, if the year is divisible by 4 but not divisible by 100, you don't tell your caller whether or not that is a leap year. – Aspergillus

if(!yearr(year)) { printf("It is a leap year."); } else { printf("It is not a leap year"); } Instead of the above one if(yearr(year)) { printf("It is not a leap year."); } else { printf("It is a leap year"); } Don't you think the below one is easy to understand? – Savarin

From K&R Section 2.5: (year % 4 == 0 && year % 100 != 0) || year % 400 == 0 – Touchback

Answer 1

Your logic to determine a leap year is wrong. This should get you started (from Wikipedia):

if year modulo 400 is 0
       then is_leap_year
else if year modulo 100 is 0
       then not_leap_year
else if year modulo 4 is 0
       then is_leap_year
else
       not_leap_year

x modulo y means the remainder of x divided by y. For example, 12 modulo 5 is 2.

Mirage

See how this is discussed here. – Thenceforth

Answer 2

Most efficient leap year test:

if ((year & 3) == 0 && ((year % 25) != 0 || (year & 15) == 0))
{
    /* leap year */
}

This code is valid in C, C++, C#, Java, and many other C-like languages. The code utilizes a single TRUE/FALSE expression that consists of three separate tests:

• 4th year test: year & 3
• 100th year test: year % 25
• 400th year test: year & 15

A complete discussion of how this code works appears below, but first a discussion of Wikipedia's algorithm is called for:

Wikipedia algorithm is INEFFICIENT/UNRELIABLE

Wikipedia has published a pseudo-code algorithm (See: Wikipedia: Leap year - Algorithm) that has been subjected to constant editing, opinion, and vandalism.

DO NOT IMPLEMENT WIKIPEDIA ALGORITHM!

One of the longest-standing (and inefficient) Wikipedia algorithms appeared as follows:

if year modulo 400 is 0 then
   is_leap_year
else if year modulo 100 is 0 then
   not_leap_year
else if year modulo 4 is 0 then
   is_leap_year
else
   not_leap_year

The above algorithm is inefficient because it always performs the tests for the 400th year and 100th year even for years that would quickly fail the "4th year test" (the modulo 4 test)—which is 75% of the time! By re-ordering the algorithm to perform the 4th year test first we speed things up significantly.

"MOST-EFFICIENT" PSEUDO-CODE ALGORITHM

I provided the following algorithm to Wikipedia (more than once):

if year is not divisible by 4 then not leap year
else if year is not divisible by 100 then leap year
else if year is divisible by 400 then leap year
else not leap year

This "most-efficient" pseudo-code simply changes the order of tests so the division by 4 takes place first, followed by the less-frequently occurring tests. Because "year" does not divide by four 75-percent of the time, the algorithm ends after only one test in three out of four cases.

NOTE: I have fought various Wikipedia editors to improve the algorithm published there, arguing that many novice—and professional—programmers quickly arrive at the Wikipedia page (due to top search engine listings) and implement the Wikipedia pseudo-code without any further research. Wikipedia editors repudiated and deleted every attempt I made to improve, annotate or even merely footnote the published algorithm. Apparently, they feel finding efficiencies is the programmer's problem. That may be true, but many programmers are too hurried to perform solid research!

DISCUSSION OF "MOST-EFFICIENT" LEAP YEAR TEST

Bitwise-AND in place of modulo:

I have replaced two of the modulo operations in the Wikipedia algorithm with bitwise-AND operations. Why and how?

Performing a modulo calculation requires division. One doesn't often think twice about this when programming a PC, but when programming 8-bit microcontrollers embedded in small devices you may find that a divide function cannot be natively performed by the CPU. On such CPUs, division is an arduous process involving repetitive looping, bit shifting, and add/subtract operations that is very slow. It is very desirable to avoid.

It turns out that the modulo of powers of two can be alternately achieved using a bitwise-AND operation (see: Wikipedia: Modulo operation - Performance Issues):

x % 2^n == x & (2^n - 1)

Many optimizing compilers will convert such modulo operations to bitwise-AND for you, but less advanced compilers for smaller and less popular CPUs may not. Bitwise-AND is a single instruction on every CPU.

By replacing the modulo 4 and modulo 400 tests with & 3 and & 15 (see below: 'Factoring to reduce math') we can ensure that the fastest code results without using a much slower divide operation.

There exists no power of two that equals 100. Thus, we are forced to continue to use the modulo operation for the 100th year test, however 100 is replaced by 25 (see below).

Factoring to simplify the math:

In addition to using bitwise-AND to replace modulo operations, you may note two additional disputes between the Wikipedia algorithm and the optimized expression:

• modulo 100 is replaced by modulo 25
• modulo 400 is replaced by & 15

The 100th year test utilizes modulo 25 instead of modulo 100. We can do this because 100 factors out to 2 x 2 x 5 x 5. Because the 4th year test already checks for factors of 4 we can eliminate that factor from 100, leaving 25. This optimization is probably insignificant to nearly every CPU implementation (as both 100 and 25 fit in 8-bits).

The 400th year test utilizes & 15 which is equivalent to modulo 16. Again, we can do this because 400 factors out to 2 x 2 x 2 x 2 x 5 x 5. We can eliminate the factor of 25 which is tested by the 100th year test, leaving 16. We cannot further reduce 16 because 8 is a factor of 200, so removing any more factors would produce a unwanted positive for a 200th year.

The 400th year optimization is greatly important to 8-bit CPUs, first, because it avoids division; but, more important, because the value 400 is a 9-bit number which is much more difficult to deal with in an 8-bit CPU.

Short-circuit Logical AND/OR operators:

The final, and most important, optimization used are the short-circuit logical AND ('&&') and OR ('||') operators (see: Wikipedia: Short-circuit evaluation), which are implemented in most C-like languages. Short-circuit operators are so named because they do not bother to evaluate the expression on the right side if the expression on the left side, by itself, dictates the outcome of the operation.

For example: If the year is 2003, then year & 3 == 0 is false. There is no way that the tests on the right side of the logical AND can make the outcome true, so nothing else gets evaluated.

By performing the 4th year test first, only the 4th year test (a simple bitwise-AND) is evaluated three-quarters (75 percent) of the time. This speeds up program execution greatly, especially since it avoids the division necessary for the 100th year test (the modulo 25 operation).

NOTE ON PARENTHESES PLACEMENT

One commenter felt parentheses were misplaced in my code and suggested the sub-expressions be regrouped around the logical AND operator (instead of around the logical OR), as follows:

if (((year & 3) == 0 && (year % 25) != 0) || (year & 15) == 0) { /* LY */ }

The above is incorrect. The logical AND operator has higher precedence than logical OR and will be evaluated first with or without the new parentheses. Parentheses around the logical AND arguments has no effect. This might lead one to eliminate the sub-groupings entirely:

if ((year & 3) == 0 && (year % 25) != 0 || (year & 15) == 0) { /* LY */ }

But, in both cases above, the right side of the logical OR (the 400th year test) is evaluated almost every time (i.e., years not divisible by 4 and 100). Thus, a useful optimization has been mistakenly eliminated.

The parentheses in my original code implement the most optimized solution:

if ((year & 3) == 0 && ((year % 25) != 0 || (year & 15) == 0)) { /* LY */ }

Here, the logical OR is only evaluated for years divisible by 4 (because of the short-circuit AND). The right side of the logical OR is only evaluated for years divisible by 4 and 100 (because of the short-circuit OR).

NOTE FOR C/C++ PROGRAMMERS

C/C++ programmers might feel this expression is more optimized:

if (!(year & 3) && ((year % 25) || !(year & 15))) { /* LY */ }

This is not more optimized! While the explicit == 0 and != 0 tests are removed, they become implicit and are still performed. Worse, the code is no longer valid in strongly-typed languages like C# where year & 3 evaluates to an int, but the logical AND (&&), OR (||) and NOT (!) operators require bool arguments.

Jessie

@tarabyte Very kind. Thank you. Now, if we can get Wikipedia to publish a better article for the world's benefit... – Jessie

I understand the efficiency argument, but why do you label Wikipedia's algorithm as "unreliable". In what edge case does it fail? – Dent

@EricJ. Wikipedia is unreliable because it is constantly edited by anonymous individuals. I have seen incorrect algorithm edits. WP is not a credible source of information, and is often wrong or opinion oriented. It should be viewed as conversive, but not canonical. – Jessie

With added 4000th test: int IsLeapYear(int y){ return ( ((y & 3) == 0) && (y % 25 != 0 ) ) || ( ((y & 15) == 0) && (y % 4000 != 0) ); } – Woolworth

@Woolworth See my "Note on parenthesis placement". I believe you erred in your sub-groupings. Also, I'm fairly certain you can optimize y % 4000 -- the only time that sub-expression should be evaluated is y = 400,800,1200,1600,...,4000. Perhaps, (y << 5) % 125? Maybe not. I'd need to think on it. I imagine few people care about the 4000th year test, though. Thx! – Jessie

@KevinP.Rice Well, that code was part of my uni homework and was thoroughly tested and accepted. However, I agree with you that in real world the test doesn't have many uses. – Woolworth

@Woolworth While I'm sure your code works, the parentheses placement is errant. The 400th year test is needlessly evaluated even when the 4th year test fails. You eliminated the short-circuit optimization of the first logical AND. – Jessie

@KevinP.Rice Oh, I get your point now, here should be the fixed version. Thanks for noticing that, this code is also part of my snippets library and I'm always looking for ways to improve it. – Woolworth

@KevinP.Rice: Fabulous explanation. Only comment: year & 15 can be replaced by year & 12 since it's only the 3rd bit (4) or 4th bit (8) that could be set at this point. – Dark

@CharlesPlager Thank you. I believe, when I authored this, I did realize using a smaller integer is possible. I really like your astuteness here! I appreciate that you took time to work through the logic and check my work. However, the change doesn't reduce the number of bits in the operand. Therefore, in my opinion, it would be a pointless obfuscation, not an optimization. – Jessie

There is a problem in this algorithm : ideone.com/GwbwUu, 1300 was a leap year but it does not work for 1300. – Furtherance

@Furtherance 1300 was not a leap year. It fails the 100th year test. – Jessie

@KevinP.Rice according to Wikipédia, it was : en.wikipedia.org/wiki/1300 Year 1300 (MCCC) was a leap year starting on Friday – Furtherance

@Furtherance In the modern Gregorian calendar, 1300 is not a leap year. If you have a need to go back that far in history, then you're going to have to determine what date you should be using the Julian calendar. Since this date varies with different cultures, and because other cultures used an entirely different calendar system, this is not a trivial matter. The algorithm is correct for the Gregorian calendar. – Jessie

Any idea how to optimize Tomohiko Sakamoto's weekday algorithm? – Conchology

@rindeal: the 4000 year adjustment is purely hypothetical: In the 19th century, Sir John Herschel proposed a modification to the Gregorian calendar with 969 leap days every 4000 years, instead of 970 leap days that the Gregorian calendar would insert over the same period. This would reduce the average year to 365.24225 days. Herschel's proposal would make the year 4000, and multiples thereof, common instead of leap. While this modification has often been proposed since, it has never been officially adopted. – Felicefelicia

nice detailed write-up, thanks! One addition, if you are using C, C++, or Javascript, you can avoid the tests with zero (since 0 evaluates to false, and 1 evaluates to true): !(year & 3) && ((year % 25) || !(year & 15)) Then, taking advantage of operator precedence, this can be code-golfed down to: !(y&3||!(y%25)&&y&15) ... you know, for fun! – Gayn

@Gayn I addressed eliminating the '==' test in the last section of my write-up. It's less efficient. The integer result still needs to be computed, then it must be type cast to Boolean, then tested. Don't confuse fewer characters with efficiency. Same thing with eliminating all the spaces in your code-golfing. I'm a big fan of readability. I didn't analyze your changes to the Boolean evaluation of the code you present, but it's not as efficient... The ||-operator requires evaluation of the RHS 3 times out of 4, vs. 1 in 4 using &&. – Jessie

It would be nice to see timings for how much faster the 2 approaches are – Edi

@Edi "It would be nice to see timings for how much faster the 2 approaches are" -- timings are ENTIRELY dependent on your implementation/coding of the algorithm. This is the "most efficient" algorithm. That's not the same as the most efficient code. Your compiler may not emit the best code. – Jessie

@KevinP.Rice would still be nice to see with your implementation/coding of the algorithm what the relative performance was like compared to the Wikipedia version – Edi

@Edi I forgot most of my formal training in Big-O notation, but the Wikipedia algorithm is < O(3) and my algorithm is > O(1.25). So, more than twice as fast. However, the point of this exercise wasn't initially speed. It was Wikipedia promulgating an erroneous algorithm. But if you're going to promulgate something accurate for people to use over and over, why not also make it the most efficient? – Jessie

Answer 3

Many answers talk about performance. None shows any measurement. A nice quote from gcc's documentation on __builtin_expect says this:

Programmers are notoriously bad at predicting how their programs actually perform.

Most implementations use short-circuiting of && and || as an optimization tool and go on to prescribe the "right" order for the divisibility checks for "best" performance. It is worth mentioning that short-circuiting is not necessarily an optimization feature.

Agreed, some checks might give a definitive answer (e.g. year is not multiple of 4) and make useless the subsequent tests. It seems all reasonable to immediately return at this point rather than keeping going with needless calculations. On the other hand, early returns introduce branches and this might decrease performance. (See this legendary post.) The trade-off between a branch misprediction and an unnecessary calculation is very hard to guess. Indeed, it depends on the hardware, on input data, on the exactly assembly instructions emitted by the compiler (which might change from one version to another), etc.

The sequel shall show measurements obtained in quick-bench.com. In all cases, we measure the time taken to check whether each value stored in an std::array<int, 65536> is a leap year or not. The values are pseudo-random, uniformly distributed in the interval [-400, 399]. More precisely, they are generated by the following code:

auto const years = [](){
  std::uniform_int_distribution<int> uniform_dist(-400, 399);
  std::mt19937 rng;
  std::array<int, 65536> years;
  for (auto& year : years)
    year = uniform_dist(rng);
  return years;
}();

Even when possible, I do not replace % with & (e.g. year & 3 == 0 instead of year % 4 == 0). I trust the compiler (GCC-9.2 at -O3) will do that for me. (It does.)

4-100-400 tests

Checks for leap years are, usually, written in terms of three divisibility tests: year % 4 == 0, year % 100 != 0 and year % 400 == 0. The following is a list of implementations covering all possible orders in which these checks can appear. Each implementation is prefixed with a corresponding label. (Some orders allow two different implementations, in which case, the 2nd one gets a suffix b.) They are:

b4_100_400  : year % 4 == 0 && (year % 100 != 0 || year % 400 == 0)
b4_100_400b : (year % 4 == 0 && year % 100 != 0) || year % 400 == 0
b4_400_100  : year % 4 == 0 && (year % 400 == 0 || year % 100 != 0)
b100_4_400  : (year % 100 != 0 && year % 4 == 0) || year % 400 == 0
b100_400_4  : (year % 100 != 0 || year % 400 == 0) && year % 4 == 0
b400_4_100  : year % 400 == 0 || (year % 4 == 0 && year % 100 != 0)
b400_100_4  : year % 400 == 0 || (year % 100 != 0 && year % 4 == 0)
b400_100_4b : (year % 400 == 0 || year % 100 != 0) && year % 4 == 0

The results are shown below. (See them live.)

Contrarily to what many have advised, checking divisibility by 4 first does not seem to be the best thing to do. At the contrary, at least in these measurements, the three first bars are among the worst five. The best is

b100_400_4  : (year % 100 != 0 || year % 400 == 0) && year % 4 == 0

4-25-16 tests

Another provided tip (which I must confess I thought was a good one) is replacing year % 100 != 0 with year % 25 != 0. This doesn't affect correctness since we also check year % 4 == 0. (If a number is multiple of 4 then divisibility by 100 is equivalent to divisibility by 25.) Similarly, year % 400 == 0 can be replaced with year % 16 == 0 due to the presence of divisibility check by 25.

As in the last section, we have 8 implementations using 4-25-16 divisibility checks:

b4_25_16  : year % 4 == 0 && (year % 25 != 0 || year % 16 == 0)
b4_25_16b : (year % 4 == 0 && year % 25 != 0) || year % 16 == 0
b4_16_25  : year % 4 == 0 && (year % 16 == 0 || year % 25 != 0)
b25_4_16  : (year % 25 != 0 && year % 4 == 0) || year % 16 == 0
b25_16_4  : (year % 25 != 0 || year % 16 == 0) && year % 4 == 0
b16_4_25  : year % 16 == 0 || (year % 4 == 0 && year % 25 != 0)
b16_25_4  : year % 16 == 0 || (year % 25 != 0 && year % 4 == 0)
b16_25_4b : (year % 16 == 0 || year % 25 != 0) && year % 4 == 0

Results (live here):

Again, checking divisibility by 4 first does not look a good idea. In this round the fast is

b25_16_4  : (year % 25 != 0 || year % 16 == 0) && year % 4 == 0

4-100-400 tests (no branching)

As previously mentioned branching might degrade performance. In particular, short-circuiting might be counterproductive. When this is the case, a classical trick is replacing logical operators && and || with their bit-wise counterparts & and |. The implementations become:

nb4_100_400  : (year % 4 == 0) & ((year % 100 != 0) | (year % 400 == 0))
nb4_100_400b : ((year % 4 == 0) & (year % 100 != 0)) | (year % 400 == 0)
nb4_400_100  : (year % 4 == 0) & ((year % 400 == 0) | (year % 100 != 0))
nb100_4_400  : ((year % 100 != 0) & (year % 4 == 0)) | (year % 400 == 0)
nb100_400_4  : ((year % 100 != 0) | (year % 400 == 0)) & (year % 4 == 0)
nb400_4_100  : (year % 400 == 0) | ((year % 4 == 0) & (year % 100 != 0))
nb400_100_4  : (year % 400 == 0) | ((year % 100 != 0) & (year % 4 == 0))
nb400_100_4b : ((year % 400 == 0) | (year % 100 != 0)) & (year % 4 == 0)

Results (live here):

A noticeable feature is that performance variation is not as pronounced as in the branching case and it makes difficult to declare a winner. We pick this one:

nb100_400_4  : ((year % 100 != 0) | (year % 400 == 0)) & (year % 4 == 0)

4-25-16 tests (no branching)

To complete the exercise, we consider the no-branching case with 4-25-16 divisibility tests:

nb4_25_16  : (year % 4 == 0) & ((year % 25 != 0) | (year % 16 == 0))
nb4_25_16b : ((year % 4 == 0) & (year % 25 != 0)) | (year % 16 == 0)
nb4_16_25  : (year % 4 == 0) & ((year % 16 == 0) | (year % 25 != 0))
nb25_4_16  : ((year % 25 != 0) & (year % 4 == 0)) | (year % 16 == 0)
nb25_16_4  : ((year % 25 != 0) | (year % 16 == 0)) & (year % 4 == 0)
nb16_4_25  : (year % 16 == 0) | ((year % 4 == 0) & (year % 25 != 0))
nb16_25_4  : (year % 16 == 0) | ((year % 25 != 0) & (year % 4 == 0))
nb16_25_4b : ((year % 16 == 0) | (year % 25 != 0)) & (year % 4 == 0)

Results (live here):

Once again, it's difficult to define the best and we select this one:

nb25_16_4  : ((year % 25 != 0) | (year % 16 == 0)) & (year % 4 == 0)

Champions League

It's now time to pick the best of each previous section and compare them:

b100_400_4  : (year % 100 != 0 || year % 400 == 0) && year % 4 == 0
b25_16_4    : (year % 25 != 0 || year % 16 == 0) && year % 4 == 0
nb100_400_4 : ((year % 100 != 0) | (year % 400 == 0)) & (year % 4 == 0)
nb25_16_4   : ((year % 25 != 0) | (year % 16 == 0)) & (year % 4 == 0)

Results (live here):

This chart suggests that short-circuiting is, indeed, an optimization but divisibility by 4 should be the last to be checked rather then the first. For better performance one should check divisibility by 100 first. This is rather surprising! After all, the latter test is never enough to decide whether the year is leap or not and a subsequent test (either by 400 or by 4) is always required.

Also surprising is that for the branching versions using simpler divisors 25 and 16 is not better than using the more intuitive 100 and 400. I can offer my "theory" which also partially explains why testing for 100 first is better than testing for 4. As many pointed out, the divisibility test by 4 splits execution into (25%, 75%) parts whereas the test for 100 splits it into (1%, 99%). It doesn't matter that after the latter check, the execution must carry on to another test because, at least, the branch predictor is more likely to guess correctly which way to go. Similarly, checking divisibility by 25 splits execution into (4%, 96%) which is more challenging for the branch predictor than (1%, 99%). It looks like that it is better to minimize the entropy of the distribution, helping the branch predictor, rather than maximizing the probability of early return.

For the no branching versions, simplified divisors do offer better performance. In this case the branch predictor plays no role and, therefore, the simpler the better. Generally, the compiler can perform better optimizations with smaller numbers.

Is this it?

Did we hit the wall and found out that

b100_400_4  : (year % 100 != 0 || year % 400 == 0) && year % 4 == 0

is the most performant check for leap years? Definitely not. We haven't for instance, mixed branching operators && or || with no branching ones & and |. Perhaps... Let's see and compare the above with two other implementations. The first is

m100_400_4 : (year % 100 != 0 || year % 400 == 0) & (year % 4 == 0)

(Notice the mix of branching || and non-branching & operators.) The second is an obscure "hack":

bool b;
auto n = 0xc28f5c29 * year;
auto m = n + 0x051eb850;
m = (m << 30 | m >> 2);
if (m <= 0x28f5c28)
  b = n % 16 == 0;
else
  b = n % 4 == 0;
return b

Does the latter work? Yes it does. Instead of giving a mathematical proof I suggest comparing the code emitted for the above with the one for this more readable source:

bool b;
if (year % 100 == 0)
  b = year % 16 == 0;
else
  b = year % 4 == 0;
return b;

in Compiler Explorer. They are almost identical, the only difference being that one uses an add instruction when the other uses a lea. This should convince you that the hack code does work (as long as the other does).

Benchmark results (live here):

Hold on, I hear you say, why not using the more readable code in the picture above? Well, I've tried and learned another lesson. When this code is inserted into the benchmark loop, the compiler looked at the source as a whole and decided to emit different code than when it sees the source in isolation. The performance was worse. Go figure!

And now? Is this it?

I don't know! There are many things that we could explore. The last section, for instance, showed yet another version using an if statement rather that short-circuiting. That could be a way to get even better performance. We could also try the ternary operator ?.

Be aware that all measurements and conclusions were based on GCC-9.2. With another compiler and/or version things might change. For instance, GCC from version 9.1 introduced a new improved algorithm for divisibility checks. Hence, older versions have different performances and the trade-off between an unnecessary calculation and a branch misprediction have likely changed.

The points that we can definitely conclude are:

1. Do not overthink. Prefer clear code over difficult to understand optimizations (unless you're a library writer offering higher level APIs for your users around very efficient implementations). After all, a hand-crafted snippet might not be the most performant option when you upgrade compiler. As ex-nihilo said in a comment, "There is little point in fussing over a piece of code like this unless it is known to be a performance bottleneck."
2. Guessing is difficult and it's better to measure.
3. Measuring is difficult but is better than guessing.
4. Short-circuiting/branching can be good for performance but it depends on many things including how much the code helps the branch predictor.
5. Code emitted for a snippet in isolation might be different when it's inlined somewhere.

Gentlemanfarmer

This was an interesting exercise, but maybe a final concluding point should be: 5. There is little point in fussing over a piece of code like this unless it is known to be a performance bottleneck. – Marquand

@exnihilo Very true. Post updated. Actually, this is the first point in order of importance. – Gentlemanfarmer

@exnihilo: You might be interested to see more solutions with a benchmark. Thank you Cassio for pointing to quick-bench.com. You saved my confinement blues :) – Felicefelicia

This is great stuff! Yet... it proclaims a result based upon a particular compiler with unknown "optimization". Mathematically, can you argue against performing the "4" test first, and still say it's not the highest performing? I don't think so. Hence, blaming the algorithm for flawed compilation seems to be a flawed analysis. Still, I like the attention to detail here!!! – Jessie

@KevinP.Rice: Thanks for your comments. I hope I can clarify some of your concerns. Although I have never seen it clearly stated, the argument for checking by 4 first seems to assume that returning earlier is better than not. I reckon this is a kind of natural assumption. However, it ignores the cost of branching which on many popular and modern hardware might have a big impact. Cost-free branching isn't the only hidden assumption that I must normally guess from arguments favoring checking by 4 first. (1/3) – Gentlemanfarmer

I can only guess the 25% probability attributed for a year to be multiple of 4 comes from a hidden assumption that year values are uniformly distributed. Although not unnatural, this should be explicitly stated. Arguably, it's also reasonable to assume that year values come from uniformly distributed dates. Since most years that are divisible by 4 are leap and hence longer than others, under the latter assumption, the probability of having a year value that is multiple of 4 is slightly over 25%. It's not difficult to come up with use cases where the probability is completely different. (2/3) – Gentlemanfarmer

My comments are against the explanation (as opposed to the statement). To mathematically argue against a statement, I must know what that is. If it's that "performing the '4' test first is (always) the highest performing", then this post is a counterexample which disproves the claim. It's based on concrete measurements on real/popular platforms and provides all details (including optimization level) allowing anyone to replicate results. The post is clear in saying that YMMV depending on data, compiler, hardware, ... If anything, I see the precision of my post as one of its strengths. (3/3) – Gentlemanfarmer

@Cassio Neri: I couldn't agree more with your comments. You are right on target. My claim of best performance is based on the algorithm in a vacuum with unknown input. In that case, 75% of cases are eliminated by the first test. If you know more about your particular use case or machine architecture, then the best solution might change, of course. The cost of branching or other architectural limits effects how well the algorithm can be implemented, but the algorithm itself is still most efficient with unknown data by evaluating the "4 test" first. I love that you debunk oversimplification! – Jessie

Let me also admit here that my "most efficient" claim contains a bit of intentional marketing to garner interest in the topic. I'm extremely happy about the ongoing interest in my eight year old work. I remain very frustrated with Wikipedia's resistance to publishing a better algorithm, given that Wikipedia is a go-to source for the hoards and masses. I feel a really good, well-vetted code snippet should be widely accepted and published... Not that this tiny bit of code affects the world in any great way over inefficient code... But why not promulgate the best possible code? – Jessie

@exnihilo If you felt "fussing over a piece of code" was the point of my exercise, I didn't communicate well. Something as ubiquitous as leap-year should be a well-accepted snippet, not something reinvented (often with bugs). My "most efficient" title doesn't say "highest performing". The claim was merely proffered to say, "Here is a proper algorithm that is well though-out, bug free (unlike Wikipedia), high performance, and one line copy-and-paste." The point is, "Don't fuss—use this one." – Jessie

+1, but I would love to see an explanation of how the "hack" approximates year % 100 == 0. It clearly does. I just don't understand how. – Mafalda

@HowardHinnant It uses a technique called modular inverse which has been implemented in clang and gcc since versions 9.x (for both). Ideally I did not need to use that and just let the compiler do its business but, as I said in the post, for some reason the emitted code was different when the snippet above was not seen in isolation but instead in the context of the benchmark code (that is inside the measurement loop). Things might have changed since I wrote this post. (1/2) – Gentlemanfarmer

I wrote about the modular inverse algorithm here. The article covers the main idea in the case of unsigned integers (signed integers need an extra step). If we can afford to work with years that are not in the full 32-bits ranges (like in std::chrono::year) then there's another technique, which I call mcomp (for multiply and compare) which is even more efficient. I wrote about it here. Again, this covers unsigned ints and signed ones need to be adapted (2/2) – Gentlemanfarmer

@CassioNeri I revisited this yesterday... As the author of the "most efficient" algorithm, I realized your testing is flawed--you are comparing implementations of the algorithm. You aren't comparing algorithms. Compilers and machines all have various strengths and flaws. If things like branch prediction or compiler attempts at optimization cause a slow-down, that's the fault of the branch prediction or compiler, not an inefficiency in the algorithm. The more we know about a machine, the better we can write code. But that's not the algorithm. I love your work here, though! – Jessie

On CPython 3.11.1/macOS/M1 b4_25_16 and b4_100_400 are joint fastest gist.github.com/moreati/1893473720b7399073e43b2770724d1f – Petr

Answer 4

int isLeapYear(int year)
{
   return (year % 400 == 0) || ( ( year % 100 != 0) && (year % 4 == 0 ));
}

Slavin

Inefficiency, primarily due to the order of execution. Mod 400 and Mod 100 must be calculated every time, when the Mod 4 term could have ruled those out 75% of the time (see my answer above). Minor? Yes, in the scheme of things. However, when looking for a reference answer, the Wikipedia algorithm is too-often repeated as a good one (and it isn't very good at all). To some, this detail isn't important, but to me the Wikipedia algorithm is like writing 2/4ths instead of 1/2. – Jessie

@KevinP.Rice, 2 year old question but I'll bite. If you see OP's code, he's clearly a beginner and never really asked for an efficient implementation. Given the context, If i was a teacher, I'd never recommend the OP to use your answer. Besides, I'd always pick readable code over micro-optimized code any day. But to each his own. Cheers! – Slavin

Cheers back! I wouldn't call reversing the order of the terms (put year % 4 first) micro-optimizing, nor would I call the use of modulo especially beginner friendly or readable in the first place. I'm not a disciple of "all code must be plainly understandable"---that's what code comments are for, and I comment my code LIBERALLY! If the most efficient algorithm was well-published to the point of being as canonical as E=MC2, then no one would challenge it's readability. Instead, the weak algorithm on Wikipedia has become canonical and the world stands still. Rant done. Happy St.P Day! – Jessie

Answer 5

Although the logic that divides by 400 first is impeccable, it is not as computationally efficient as dividing by 4 first. You can do that with the logic:

#define LEAPYEAR(y) (((y) % 4) == 0 && (((y) % 100) != 0 || ((y) % 400) == 0))

This divides by 4 for every value, but for 3/4 of them, the testing terminates there. For the 1/4 that pass the first test, it then divides by 100, eliminating 24/25 values; for the remaining 1 out of a 100, it divides by 400 too, coming up with a final answer. Granted, this is not a huge saving.

Aspergillus

You should replace y % 4 with y & 3, and replace y % 400 with y & 15. Rationale: modulus division is slow on some platforms whereas a single bitwise-AND is typically one instruction cycle. Some language compilers perform this optimization automatically, but baking it into the code guarantees it. Modulo 400 is able to be replaced with & 15 because 16 is a factor of 400 but not 100 (or 200). For 8-bit systems, the & 15 is much easier to deal with. Technically, % 100 can be replaced with % 25 but this is not likely an improvement for any system. – Jessie

@Kevin P. Rice Will replacing y % 4 with y & 3 work correctly if the integers are not 2's complement and y < 0? – Widgeon

@KevinP.Rice: The switch from Julian to Gregorian is a good bit more complex than "it happened in 1582". Many Roman Catholic countries changed in 1584; countries under British sway changed in 1752; other countries changed at different times (Russia in the 20th century; the Russian Orthodox church still hasn't changed, AFAIK). Check the output from cal 9 1752 on a Unix-ish machine. Also, for negative values of year, you have to wrestle with the presence or absence of a year 0. – Aspergillus

@chux [REPOST] No. Negative modulo 4 values (i.e., -4, -8, -12, ...) are represented in two's complement binary with the last two digits being zero. This doesn't work for one's complement representations. Keep in mind also, use of this algorithm would be improper for y < 1582 as the Gregorian calendar wasn't introduced until the year 1582. Further complications are pointed out by @JonathanLeffler (supra). – Jessie

@KevinP.Rice: It seems I mis-remembered 1584 as being special; it was indeed in 1582 that Pope Gregory decreed the use of the Gregorian calendar, and most Roman Catholic countries put it into effect in that year, but not all. – Aspergillus

@Kevin P. Rice y < 1582 makes sense with Proleptic_Gregorian_calendar. This is much like using year 1 or 100 as the Julian/Gregorian calender using AD year was not developed until centuries later maybe 300-400. – Widgeon

@chux Historical calendars and regional variations aside, just know for positive integers and two's complement negative integers y % 4 is equivalent to y & 3. More generally, y % pow(2, n) is equivalent to y & pow(2, n) - 1. – Jessie

Answer 6

This could be the right solution. Algorithm given on Wikipedia is not right.

-(BOOL)isLeapYear: (int)year{    

    if(year%4==0){
      if(year%100!=0){
        return YES;
     }
     else if(year%400!=0){
        return YES;
     }
     else return NO;
   }

    else return NO;
  }

Newcomer

Answer 7

From Wikipedia article on Leap year:

if (year modulo 4 is 0) and (year modulo 100 is not 0) or (year modulo 400 is 0)
   then is_leap_year
else
   not_leap_year

Implacable

Yes, this is the fact. nice one – Dominicadominical

Answer 8

The problem with your code is that you are returning a non-zero value from yearr if you think that the year is a leap year. So you don't need the ! in your if statement.

Mecke

Answer 9

http://www.wwu.edu/depts/skywise/leapyear.html

Leap Year Rules

There is a leap year every year whose number is perfectly divisible by four - except for years which are both divisible by 100 and not divisible by 400. The second part of the rule effects century years. For example; the century years 1600 and 2000 are leap years, but the century years 1700, 1800, and 1900 are not. This means that three times out of every four hundred years there are eight years between leap years.

Unknown

Answer 10

 if(year%400 ==0 || (year%100 != 0 && year%4 == 0))
    {
        printf("Year %d is a leap year",year);
    }
    else
    {
        printf("Year %d is not a leap year",year);
    }

Change it like above. Also read this.

Underdone

Answer 11

    #include 
    void main(void)
    {
        int year;
        printf("Enter a year to check if it is Leap Year\n");
        scanf("%d",&year);
        if(year%400==0) /* Why  mod 400 */
            printf("%d is a Leap Year\n",year);
        else if(year%100==0) /*  Why  mod 100  */
            printf("%d is not a Leap Year\n",year);
        else if(year%4==0)
            printf("%d is a Leap Year\n",year);
        else
            printf("%d is not a Leap Year\n",year);

    }

Boise

Answer 12

I used this code:

#include <stdio.h>

int main()
{
    int yr;
    printf ("Enter a year \n");
    scanf ("%d", &yr);

    if (yr%400 == 0)
        printf("\n LEAP YEAR.");

    else if (yr%4==0 && yr%100!=0)
        printf("\n LEAP YEAR.");
    else
        printf ("\n NOT LEAP YEAR.");
}

Chericheria

Answer 13

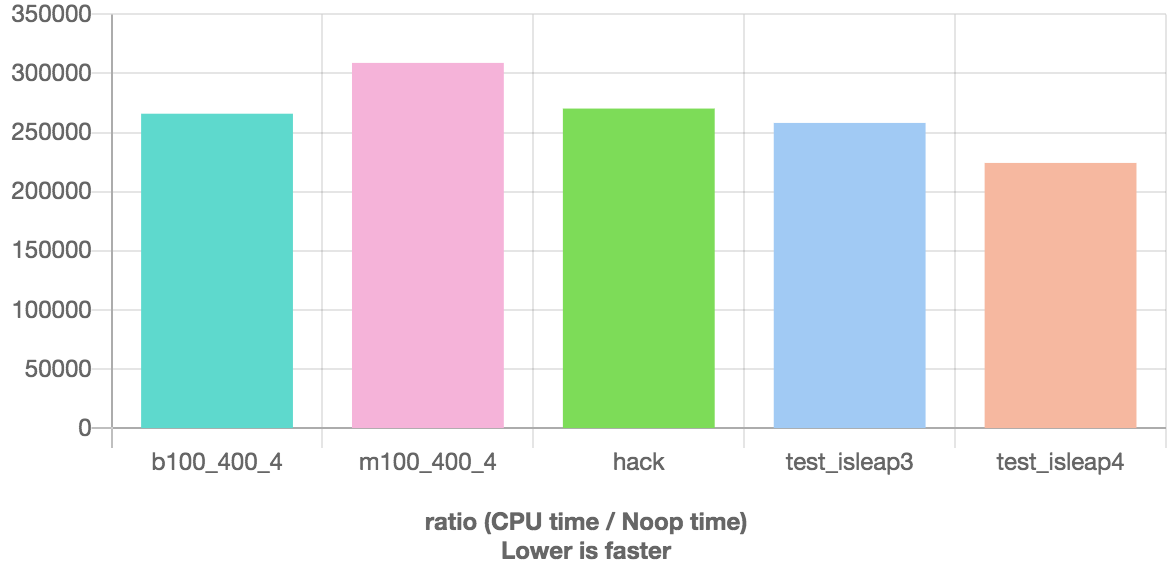
Here are 2 more solutions that seem to beat previous ones on the quick-bench.com benchmark.

This one has a test but that compiles to branchless code with clang:

int isleap3(int year) {
    unsigned y = year + 16000;
    return (y % 100) ? !(y % 4) : !(y % 16);
}

This one uses a single modulo operation and no tests, and compiles to just 2 multiplications:

static unsigned char const leaptest[400] = {
    1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,
    0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,
    0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,
    0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,
    0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,
    0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,
    0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,
    0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,
    0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,
    0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,
    0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,
    0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,
    0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,
    0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,
    0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,
    0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,
};
int isleap4(int year) {
    unsigned y = year + 16000;
    return leaptest[y % 400];
}

clang 64-bit Assembly:

isleap3:                                # @isleap3
        add     edi, 16000
        imul    eax, edi, -1030792151
        ror     eax, 2
        cmp     eax, 42949673
        mov     eax, 15
        mov     ecx, 3
        cmovb   ecx, eax
        xor     eax, eax
        test    ecx, edi
        sete    al
        ret
isleap4:                                # @isleap4
        add     edi, 16000
        imul    rax, rdi, 1374389535
        shr     rax, 39
        imul    eax, eax, 400
        sub     edi, eax
        movzx   eax, byte ptr [rdi + leaptest]
        ret
leaptest:
        .asciz  "\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\000\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\000\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\000\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000\000\001\000\000"

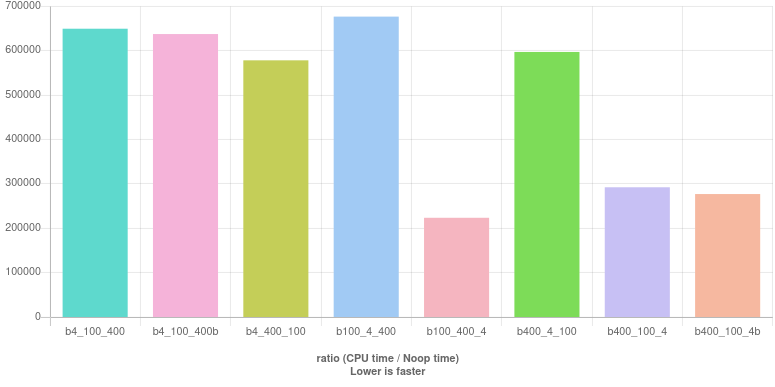
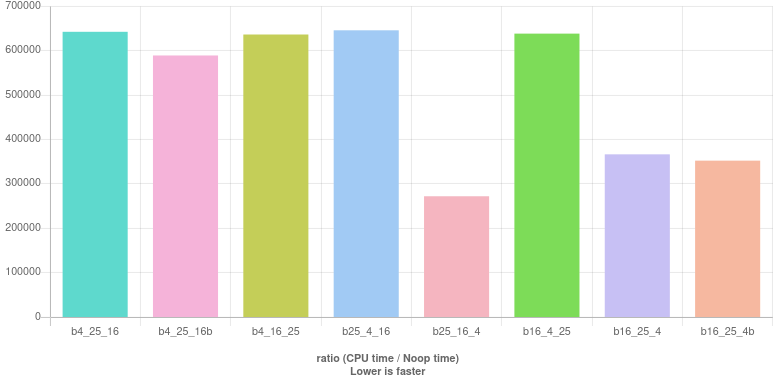
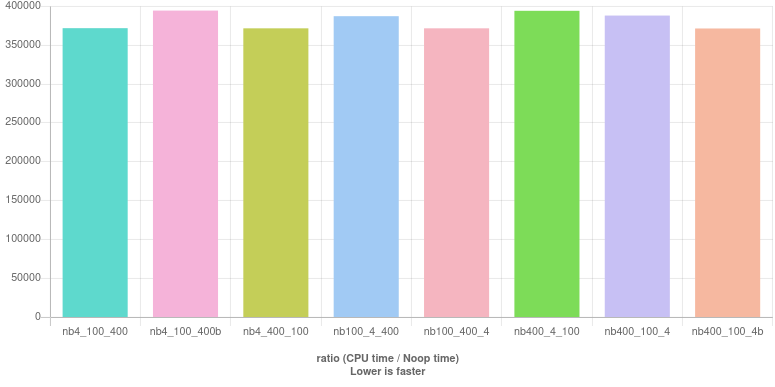
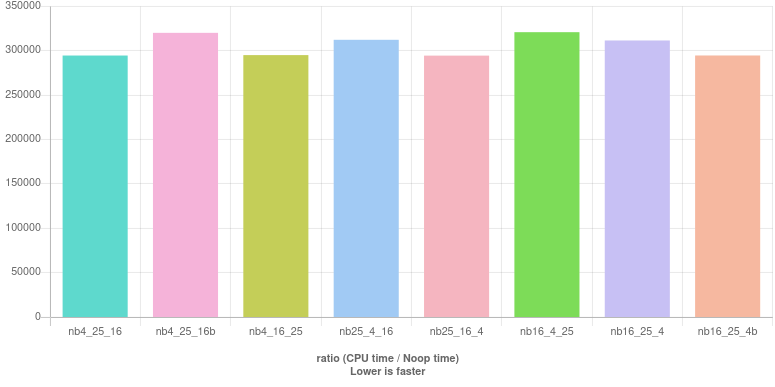
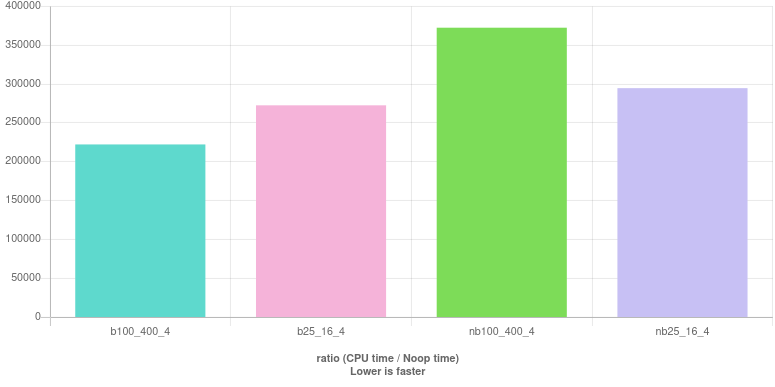
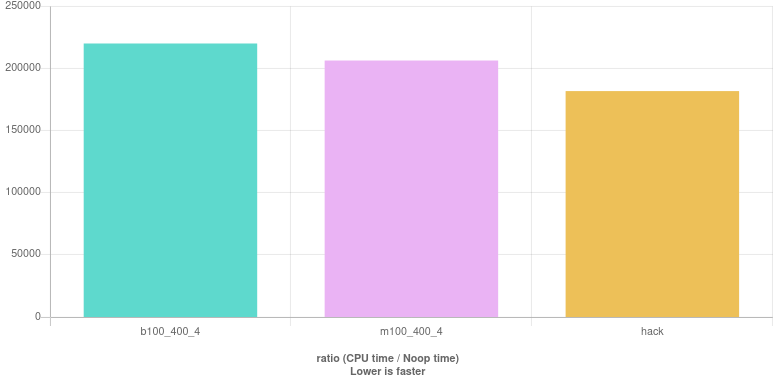
Here is the are the benchmark results:

Felicefelicia

This is interesting! Using ? is a good idea to get the cmove. (Unfortunately, in contrast to clang, gcc branches.) Using unsigned is a good idea since for many operations (notably %) it's faster than int. – Gentlemanfarmer

However your implementations do not work in the whole range of integers. For instance, isleap3 for y = -16100 returns true but -16100 is not a leap year. (See here.) If year is large enough, then year + 16000 overflows which is undefined behavior for int. (To fix this issue you could do year + 16000u to force the cast to unsigned before the computation is performed.) Forgive my preciousness, after all, who needs checking for leap years before 16000 and years that are large enough for the overflow to happen? – Gentlemanfarmer

Now, disregard the issues above and consider the following puzzle. (I honestly don't know the answer.) When I saw isleap3 I thought that I could improve it by replacing y % 100 with y % 25 because this would remove the ror instruction. I'm right as we can see here. However, the performance degrades as we can see here. How come? isleap3 performs the same instructions as isleap3_modified in addition to ror. How on Earth can the former be faster than the latter? – Gentlemanfarmer

(In my second comment I meant "before -16000".) – Gentlemanfarmer

Answer 14

As other have also mentioned condition for leap year is not correct. It should:

int yearr(int year)  
{  
    if(((year%4 == 0) && (year%100 !=0)) || (year%400==0))  
        return 1;    
    else    
        return 0;    
}  

Read it here how to check leap year in C.

Dita

Answer 15

Kevin's answer provides an optimal 8 operation test (with XOR using constants) but if you are looking for something a bit more readable, try this 9 operation test.

year % 4 == 0 && !((year % 100 == 0) ^ (year % 400 == 0))

Truth table for (year % 100 == 0) ^ (year % 400 == 0)

                              (year % 100 == 0) ^ (year % 400 == 0)
100 doesnt divide year     .    F
only 100 divides year      .    T
100 and 400 divides year   .    F

Now !(year % 100 == 0) ^ (year % 400 == 0) gives what you want.

Wages

Actually, I use bitwise-AND, not XOR. Furthermore, I replace two modulo operations (division) with bitwise-AND. On many small systems, division requires numerous CPU operations, so the savings (in my opinion) outweighs the slight difference in readability. Plus, that's what code comments are for. – Jessie

Answer 16

Calculate max/last day for month: 1..12, year: 1..3999

maxDays = month == 2 ?
  28 + ((year & 3) == 0 && ((year % 25) != 0 || (year & 15) == 0)) :
  30 + ((month & 1) ^ (month > 7));

Hoatzin

hm- somebody misses the nifty trick by XOR'ing odd/even month OFFSET, you can hardly found anywhere. – Hoatzin