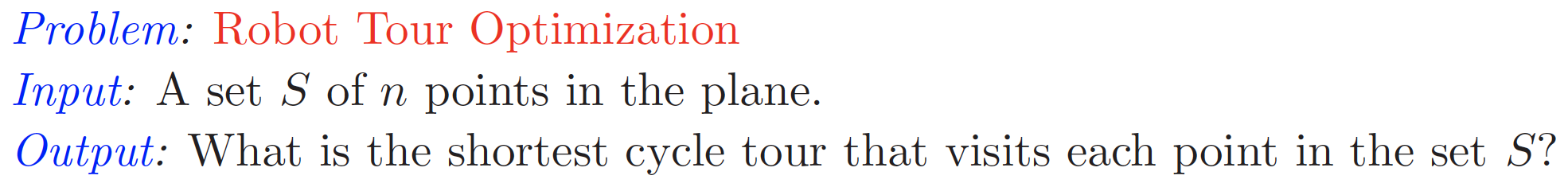What is the meaning of "from distinct vertex chains" in this nearest neighbor algorithm?

Question

The following pseudo-code is from the first chapter of an online preview version of The Algorithm Design Manual (page 7 from this PDF).

The example is of a flawed algorithm, but I still really want to understand it:

[...] A different idea might be to repeatedly connect the closest pair of endpoints whose connection will not create a problem, such as premature termination of the cycle. Each vertex begins as its own single vertex chain. After merging everything together, we will end up with a single chain containing all the points in it. Connecting the final two endpoints gives us a cycle. At any step during the execution of this closest-pair heuristic, we will have a set of single vertices and vertex-disjoint chains available to merge. In pseudocode:

ClosestPair(P)
    Let n be the number of points in set P.
    For i = 1  to n − 1 do
        d = ∞
        For each pair of endpoints (s, t) from distinct vertex chains
            if dist(s, t) ≤ d then sm = s, tm = t, and d = dist(s, t)
        Connect (sm, tm) by an edge
    Connect the two endpoints by an edge

Please note that sm and tm should be sm and tm.

First of all, I don't understand what "from distinct vertex chains" would mean. Second, i is used as a counter in the outer loop, but i itself is never actually used anywhere! Could someone smarter than me please explain what's really going on here?

Atalanti

Interesting, I was about to come up with the same questions! – Cathcart

Exactly the same questions! Word for word. I was actually depressed that I'm not smart enough for the book - well at least alone :-P thanks for posting! – Arrowwood

Is this a good book on the whole – Kohima

Answer 1

1) The description states that every vertex always belongs either to a "single-vertex chain" (i.e., it's alone) or it belongs to one other chain; a vertex can only belong to one chain. The algorithm says at each step you select every possible pair of two vertices which are each an endpoint of the respective chain they belong to, and don't already belong to the same chain. Sometimes they'll be singletons; sometimes one or both will already belong to a non-trivial chain, so you'll join two chains.

2) You repeat the loop n times, so that you eventually select every vertex; but yes, the actual iteration count isn't used for anything. All that matters is that you run the loop enough times.

Komarek

a bit of clarification for 1): they enumerate only the endpoints of the chains. It's not some kind of Kruskal's algorithm, it's a TSP heuristic, the chains grow only at the endpoints. – Literature

I get the overall idea, what I am missing is the first iteration. In the first iteration there are no endpoints so how are the single vertices enumerated upon? ex: -5, -1, 0, 2. – Roselinerosella

A Singleton is a chain with one endpoint. At the beginning each point is a Singleton. – Komarek

Thanks, you have no idea how useful your comments are given the frustration. What I meant to ask is, is there a specific order in which these points are processed. Here is my Understanding: – Roselinerosella

@dhblah perhaps my answer here would help – Warthman

Answer 2

This is how I see it, after explanation of Ernest Friedman-Hill (accepted answer):

So the example from the same book (Figure 1.4). I've added names to the vertices to make it clear

So at first step all the vertices are single vertex chains, so we connect A-D, B-E and C-F pairs, b/c distance between them is the smallest.

At the second step we have 3 chains and distance between A-D and B-E is the same as between B-E and C-F, so we connect let's say A-D with B-E and we left with two chains - A-D-E-B and C-F

At the third step there is the only way to connect them is through B and C, b/c B-C is shorter then B-F, A-F and A-C (remember we consider only endpoints of chains). So we have one chain now A-D-E-B-C-F.

At the last step we connect two endpoints (A and F) to get a cycle.

Setback

I wasn't understanding that B-E prevents A-B and E-F because only vertexes in different chains are chosen. This completed my understanding – Warthman

A picture tells a thousand words, thank you! But this part I didn't understand: "b/c distance between them is the smallest". To know that, it seems to me that you would have to iterate through all other points to figure out which of the respective distances are the smallest. – Craniotomy

@Craniotomy A-D has distance 1-e and D-E has 1+e and afaiu it's already known – Setback

It's stated in the text of the book, but the book does not explain how that is known. – Craniotomy

Answer 3

Though question is already answered, here's a python implementation for closest pair heuristic. It starts with every point as a chain, then successively extending chains to build one long chain containing all points. This algorithm does build a path yet it's not a sequence of robot arm movements for that arm starting point is unknown.

import matplotlib.pyplot as plot
import math
import random


def draw_arrow(axis, p1, p2, rad):
    """draw an arrow connecting point 1 to point 2"""
    axis.annotate("",
              xy=p2,
              xytext=p1,
              arrowprops=dict(arrowstyle="-", linewidth=0.8, connectionstyle="arc3,rad=" + str(rad)),)


def closest_pair(points):
    distance = lambda c1p, c2p:  math.hypot(c1p[0] - c2p[0], c1p[1] - c2p[1])
    chains = [[points[i]] for i in range(len(points))]
    edges = []
    for i in range(len(points)-1):
        dmin = float("inf")  # infinitely big distance
        # test each chain against each other chain
        for chain1 in chains:
            for chain2 in [item for item in chains if item is not chain1]:
                # test each chain1 endpoint against each of chain2 endpoints
                for c1ind in [0, len(chain1) - 1]:
                    for c2ind in [0, len(chain2) - 1]:
                        dist = distance(chain1[c1ind], chain2[c2ind])
                        if dist < dmin:
                            dmin = dist
                            # remember endpoints as closest pair
                            chain2link1, chain2link2 = chain1, chain2
                            point1, point2 = chain1[c1ind], chain2[c2ind]
        # connect two closest points
        edges.append((point1, point2))
        chains.remove(chain2link1)
        chains.remove(chain2link2)
        if len(chain2link1) > 1:
            chain2link1.remove(point1)
        if len(chain2link2) > 1:
            chain2link2.remove(point2)
        linkedchain = chain2link1
        linkedchain.extend(chain2link2)
        chains.append(linkedchain)
    # connect first endpoint to the last one
    edges.append((chains[0][0], chains[0][len(chains[0])-1]))
    return edges


data = [(0.3, 0.2), (0.3, 0.4), (0.501, 0.4), (0.501, 0.2), (0.702, 0.4), (0.702, 0.2)]
# random.seed()
# data = [(random.uniform(0.01, 0.99), 0.2) for i in range(60)]
edges = closest_pair(data)
# draw path
figure = plot.figure()
axis = figure.add_subplot(111)
plot.scatter([i[0] for i in data], [i[1] for i in data])
nedges = len(edges)
for i in range(nedges - 1):
    draw_arrow(axis, edges[i][0], edges[i][1], 0)
# draw last - curved - edge
draw_arrow(axis, edges[nedges-1][0], edges[nedges-1][1], 0.3)
plot.show()

Goody

Thank you for this. May I ask why the longest line is curved instead of straight? The curve makes the line longer. – Tautog

@Tautog Because if you draw it straight then it will cross previously draw lines. I believe curve makes it look a bit better. In the line second to last change the last parameter of draw_arrow to 0 if you want it to be straight. – Goody

Answer 4

TLDR: Skip to the section "Clarified description of ClosestPair heuristic" below if already familiar with the question asked in this thread and the answers contributed thus far.

Remarks: I started the Algorithm Design Manual recently and the ClosestPair heuristic example bothered me because of what I felt like was a lack of clarity. It looks like others have felt similarly. Unfortunately, the answers provided on this thread didn't quite do it for me--I felt like they were all a bit too vague and hand-wavy for me. But the answers did help nudge me in the direction of what I feel is the correct interpretation of Skiena's.

Problem statement and background: From page 5 of the book for those who don't have it (3rd edition):

Skiena first details how the NearestNeighbor heuristic is incorrect, using the following image to help illustrate his case:

The figure on top illustrates a problem with the approach employed by the NearestNeighbor heuristic, with the bottom figure being the optimal solution. Clearly a different approach is needed to find this optimal solution. Cue the ClosestPair heuristic and the reason for this question.

Book description: The following description of the ClosestPair heuristic is outlined in the book:

Maybe what we need is a different approach for the instance that proved to be a bad instance for the nearest-neighbor heuristic. Always walking to the closest point is too restrictive, since that seems to trap us into making moves we didn't want.

A different idea might repeatedly connect the closest pair of endpoints whose connection will not create a problem, such as premature termination of the cycle. Each vertex begins as its own single vertex chain. After merging everything together, we will end up with a single chain containing all the points in it. Connecting the final two endpoints gives us a cycle. At any step during the execution of this closest-pair heuristic, we will have a set of single vertices and the end of vertex-disjoint chains available to merge. The pseudocode that implements this description appears below.

---

Clarified description of ClosestPair heuristic

It may help to first "zoom back" a bit and answer the basic question of what we are trying to find in graph theory terms:

What is the shortest closed trail?

That is, we want to find a sequence of edges (e_1, e_2, ..., e_{n-1}) for which there is a sequence of vertices (v_1, v_2, ..., v_n) where v_1 = v_n and all edges are distinct. The edges are weighted, where the weight for each edge is simply the distance between vertices that comprise the edge--we want to minimize the overall weight of whatever closed trails exist.

Practically speaking, the ClosestPair heuristic gives us one of these distinct edges for every iteration of the outer for loop in the pseudocode (lines 3-10), where the inner for loop (lines 5-9) ensures the distinct edge being selected at each step, (s_m, t_m), is comprised of vertices coming from the endpoints of distinct vertex chains; that is, s_m comes from the endpoint of one vertex chain and t_m from the endpoint of another distinct vertex chain. The inner for loop simply ensures we consider all such pairs, minimizing the distance between potential vertices in the process.

Note (ties in distance between vertices): One potential source of confusion is that no sort of "processing order" is specified in either for loop. How do we determine the order in which to compare endpoints and, furthermore, the vertices of those endpoints? It doesn't matter. The nature of the inner for loop makes it clear that, in the case of ties, the most recently encountered vertex pairing with minimal distance is chosen.

Good instance of ClosestPair heuristic

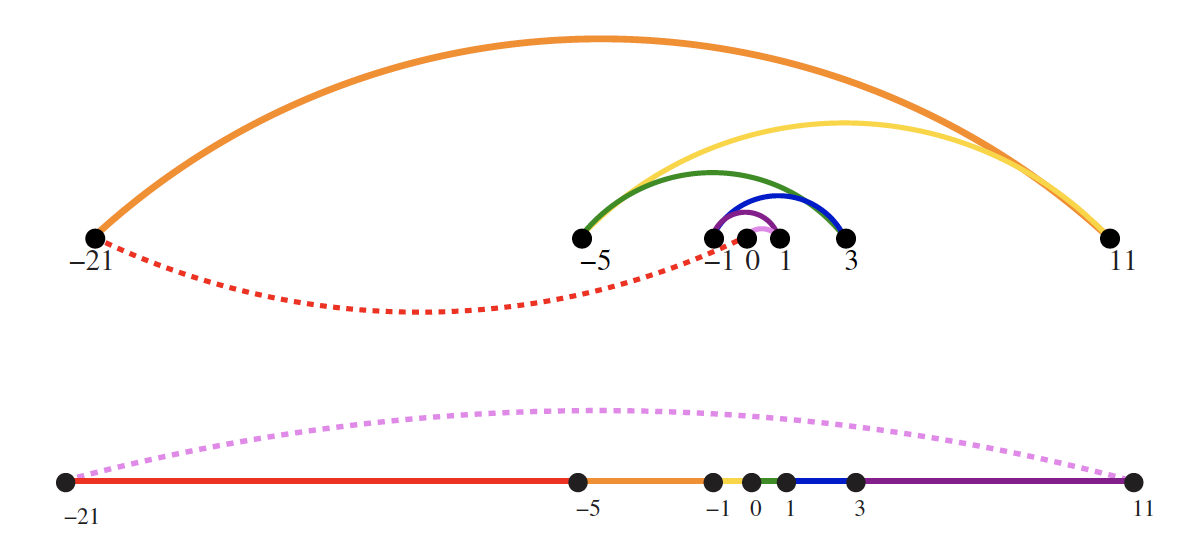
Recall what happened in the bad instance of applying the NearestNeighbor heuristic (observe the newly added vertex labels):

The total distance covered was absurd because we kept jumping back and forth over 0.

Now consider what happens when we use the ClosestPair heuristic. We have n = 7 vertices; hence, the pseudocode indicates that the outer for loop will be executed 6 times. As the book notes, each vertex begins as its own single vertex chain (i.e., each point is a singleton where a singleton is a chain with one endpoint). In our case, given the figure above, how many times will the inner for loop execute? Well, how many ways are there to choose a 2-element subset of an n-element set (i.e., the 2-element subsets represent potential vertex pairings)? There are n choose 2 such subsets:

Since n = 7 in our case, there's a total of 21 possible vertex pairings to investigate. The nature of the figure above makes it clear that (C, D) and (D, E) are the only possible outcomes from the first iteration since the smallest possible distance between vertices in the beginning is 1 and dist(C, D) = dist(D, E) = 1. Which vertices are actually connected to give the first edge, (C, D) or (D, E), is unclear since there is no processing order. Let's assume we encounter vertices D and E last, thus resulting in (D, E) as our first edge.

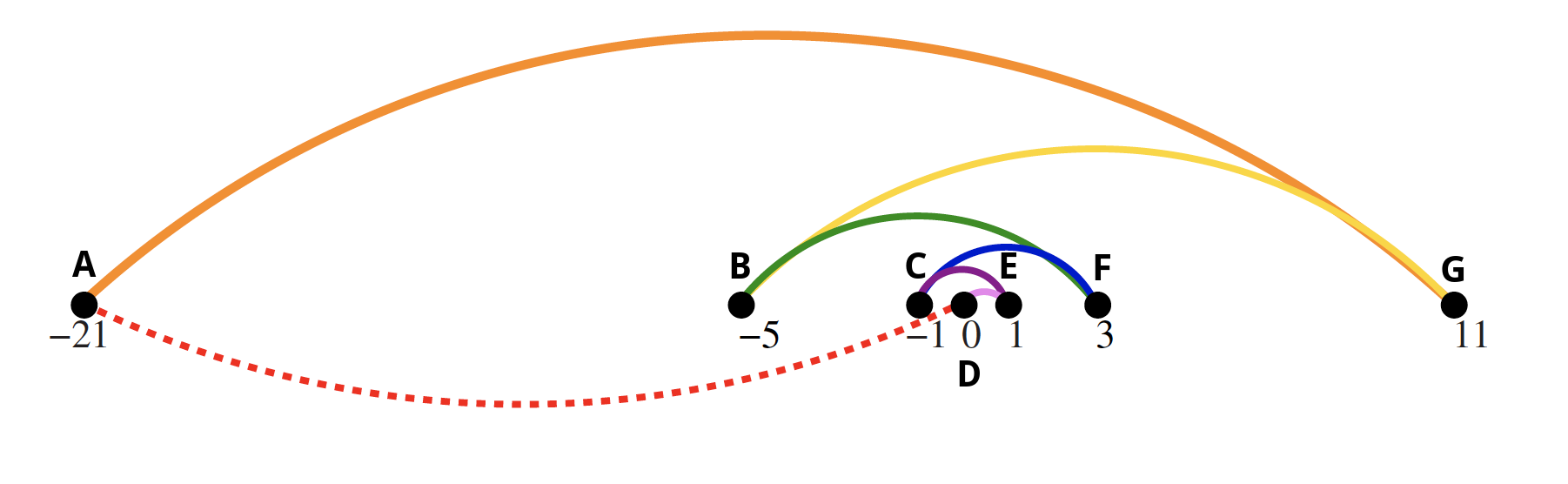
Now there are 5 more iterations to go and 6 vertex chains to consider: A, B, C, (D, E), F, G.

Note (each iteration eliminates a vertex chain): Each iteration of the outer for loop in the ClosestPair heuristic results in the elimination of a vertex chain. The outer for loop iterations continue until we are left with a single vertex chain comprised of all vertices, where the last step is to connect the two endpoints of this single vertex chain by an edge. More precisely, for a graph G comprised of n vertices, we start with n vertex chains (i.e., each vertex begins as its own single vertex chain). Each iteration of the outer for loop results in connecting two vertices of G in such a way that these vertices come from distinct vertex chains; that is, connecting these vertices results in merging two distinct vertex chains into one, thus decrementing by 1 the total number of vertex chains left to consider. Repeating such a process n - 1 times for a graph that has n vertices results in being left with n - (n - 1) = 1 vertex chain, a single chain containing all the points of G in it. Connecting the final two endpoints gives us a cycle.

One possible depiction of how each iteration looks is as follows:

ClosestPair outer for loop iterations
  1: connect D to E # -> dist: 1, chains left (6): A, B, C, (D, E), F, G
  2: connect D to C # -> dist: 1, chains left (5): A, B, (C, D, E), F, G
  3: connect E to F # -> dist: 3, chains left (4): A, B, (C, D, E, F), G
  4: connect C to B # -> dist: 4, chains left (3): A, (B, C, D, E, F), G
  5: connect F to G # -> dist: 8, chains left (2): A, (B, C, D, E, F, G)
  6: connect B to A # -> dist: 16, single chain: (A, B, C, D, E, F, G)

Final step: connect A and G

Hence, the ClosestPair heuristic does the right thing in this example where previously the NearestNeighbor heuristic did the wrong thing:

Bad instance of ClosestPair heuristic

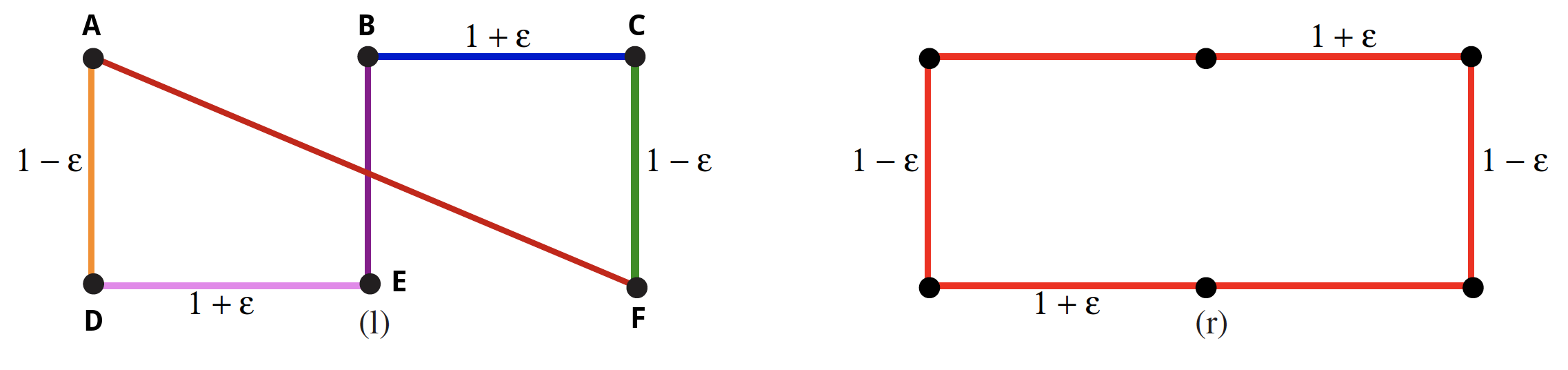
Consider what the ClosestPair algorithm does on the point set in the figure below (it may help to first try imagining the point set without any edges connecting the vertices):

How can we connect the vertices using ClosestPair? We have n = 6 vertices; thus, the outer for loop will execute 6 - 1 = 5 times, where our first order of business is to investigate the distance between vertices of

total possible pairs. The figure above helps us see that dist(A, D) = dist(B, E) = dist(C, F) = 1 - ɛ are the only possible options in the first iteration since 1 - ɛ is the shortest distance between any two vertices. We arbitrarily choose (A, D) as the first pairing.

Now are there are 4 more iterations to go and 5 vertex chains to consider: (A, D), B, C, E, F. One possible depiction of how each iteration looks is as follows:

ClosestPair outer for loop iterations
  1: connect A to D # --> dist: 1-ɛ, chains left (5): (A, D), B, C, E, F
  2: connect B to E # --> dist: 1-ɛ, chains left (4): (A, D), (B, E), C, F
  3: connect C to F # --> dist: 1-ɛ, chains left (3): (A, D), (B, E), (C, F)
  4: connect D to E # --> dist: 1+ɛ, chains left (2): (A, D, E, B), (C, F)
  5: connect B to C # --> dist: 1+ɛ, single chain: (A, D, E, B, C, F)

Final step: connect A and F

Note (correctly considering the endpoints to connect from distinct vertex chains): Iterations 1-3 depicted above are fairly uneventful in the sense that we have no other meaningful options to consider. Even once we have the distinct vertex chains (A, D), (B, E), and (C, F), the next choice is similarly uneventful and arbitrary. There are four possibilities given that the smallest possible distance between vertices on the fourth iteration is 1 + ɛ: (A, B), (D, E), (B, C), (E, F). The distance between vertices for all of the points above is 1 + ɛ. The choice of (D, E) is arbitrary. Any of the other three vertex pairings would have worked just as well. But notice what happens during iteration 5--our possible choices for vertex pairings have been tightly narrowed. Specifically, the vertex chains (A, D, E, B) and (C, F), which have endpoints (A, B) and (C, F), respectively, allow for only four possible vertex pairings: (A, C), (A, F), (B, C), (B, F). Even if it may seem obvious, it is worth explicitly noting that neither D nor E were viable vertex candidates above--neither vertex is included in the endpoint, (A, B), of the vertex chain of which they are vertices, namely (A, D, E, B). There is no arbitrary choice at this stage. There are no ties in the distance between vertices in the pairs above. The (B, C) pairing results in the smallest distance between vertices: 1 + ɛ. Once vertices B and C have been connected by an edge, all iterations have been completed and we are left with a single vertex chain: (A, D, E, B, C, F). Connecting A and F gives us a cycle and concludes the process.

The total distance traveled across (A, D, E, B, C, F) is as follows:

The distance above evaluates to 5 - ɛ + √(5ɛ^2 + 6ɛ + 5) as opposed to the total distance traveled by just going around the boundary (the right-hand figure in the image above where all edges are colored in red): 6 + 2ɛ. As ɛ -> 0, we see that 5 + √5 ≈ 7.24 > 6 where 6 was the necessary amount of travel. Hence, we end up traveling about

farther than is necessary by using the ClosestPair heuristic in this case.

Pinkard