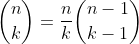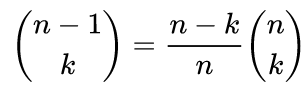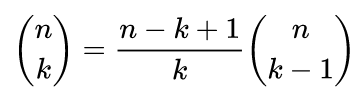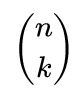For large k, we can reduce the work significantly by exploiting two fundamental facts:
If p is a prime, the exponent of p in the prime factorisation of n! is given by (n - s_p(n)) / (p-1), where s_p(n) is the sum of the digits of n in the base p representation (so for p = 2, it's popcount). Thus the exponent of p in the prime factorisation of choose(n,k) is (s_p(k) + s_p(n-k) - s_p(n)) / (p-1), in particular, it is zero if and only if the addition k + (n-k) has no carry when performed in base p (the exponent is the number of carries).
Wilson's theorem: p is a prime, if and only if (p-1)! ≡ (-1) (mod p).
The exponent of p in the factorisation of n! is usually calculated by
long long factorial_exponent(long long n, long long p)
{
long long ex = 0;
do
{
n /= p;
ex += n;
}while(n > 0);
return ex;
}
The check for divisibility of choose(n,k) by p is not strictly necessary, but it's reasonable to have that first, since it will often be the case, and then it's less work:
long long choose_mod(long long n, long long k, long long p)
{
// We deal with the trivial cases first
if (k < 0 || n < k) return 0;
if (k == 0 || k == n) return 1;
// Now check whether choose(n,k) is divisible by p
if (factorial_exponent(n) > factorial_exponent(k) + factorial_exponent(n-k)) return 0;
// If it's not divisible, do the generic work
return choose_mod_one(n,k,p);
}
Now let us take a closer look at n!. We separate the numbers ≤ n into the multiples of p and the numbers coprime to p. With
n = q*p + r, 0 ≤ r < p
The multiples of p contribute p^q * q!. The numbers coprime to p contribute the product of (j*p + k), 1 ≤ k < p for 0 ≤ j < q, and the product of (q*p + k), 1 ≤ k ≤ r.
For the numbers coprime to p we will only be interested in the contribution modulo p. Each of the full runs j*p + k, 1 ≤ k < p is congruent to (p-1)! modulo p, so altogether they produce a contribution of (-1)^q modulo p. The last (possibly) incomplete run produces r! modulo p.
So if we write
n = a*p + A
k = b*p + B
n-k = c*p + C
we get
choose(n,k) = p^a * a!/ (p^b * b! * p^c * c!) * cop(a,A) / (cop(b,B) * cop(c,C))
where cop(m,r) is the product of all numbers coprime to p which are ≤ m*p + r.
There are two possibilities, a = b + c and A = B + C, or a = b + c + 1 and A = B + C - p.
In our calculation, we have eliminated the second possibility beforehand, but that is not essential.
In the first case, the explicit powers of p cancel, and we are left with
choose(n,k) = a! / (b! * c!) * cop(a,A) / (cop(b,B) * cop(c,C))
= choose(a,b) * cop(a,A) / (cop(b,B) * cop(c,C))
Any powers of p dividing choose(n,k) come from choose(a,b) - in our case, there will be none, since we've eliminated these cases before - and, although cop(a,A) / (cop(b,B) * cop(c,C)) need not be an integer (consider e.g. choose(19,9) (mod 5)), when considering the expression modulo p, cop(m,r) reduces to (-1)^m * r!, so, since a = b + c, the (-1) cancel and we are left with
choose(n,k) ≡ choose(a,b) * choose(A,B) (mod p)
In the second case, we find
choose(n,k) = choose(a,b) * p * cop(a,A)/ (cop(b,B) * cop(c,C))
since a = b + c + 1. The carry in the last digit means that A < B, so modulo p
p * cop(a,A) / (cop(b,B) * cop(c,C)) ≡ 0 = choose(A,B)
(where we can either replace the division with a multiplication by the modular inverse, or view it as a congruence of rational numbers, meaning the numerator is divisible by p). Anyway, we again find
choose(n,k) ≡ choose(a,b) * choose(A,B) (mod p)
Now we can recur for the choose(a,b) part.
Example:
choose(144,6) (mod 5)
144 = 28 * 5 + 4
6 = 1 * 5 + 1
choose(144,6) ≡ choose(28,1) * choose(4,1) (mod 5)
≡ choose(3,1) * choose(4,1) (mod 5)
≡ 3 * 4 = 12 ≡ 2 (mod 5)
choose(12349,789) ≡ choose(2469,157) * choose(4,4)
≡ choose(493,31) * choose(4,2) * choose(4,4
≡ choose(98,6) * choose(3,1) * choose(4,2) * choose(4,4)
≡ choose(19,1) * choose(3,1) * choose(3,1) * choose(4,2) * choose(4,4)
≡ 4 * 3 * 3 * 1 * 1 = 36 ≡ 1 (mod 5)
Now the implementation:
// Preconditions: 0 <= k <= n; p > 1 prime
long long choose_mod_one(long long n, long long k, long long p)
{
// For small k, no recursion is necessary
if (k < p) return choose_mod_two(n,k,p);
long long q_n, r_n, q_k, r_k, choose;
q_n = n / p;
r_n = n % p;
q_k = k / p;
r_k = k % p;
choose = choose_mod_two(r_n, r_k, p);
// If the exponent of p in choose(n,k) isn't determined to be 0
// before the calculation gets serious, short-cut here:
/* if (choose == 0) return 0; */
choose *= choose_mod_one(q_n, q_k, p);
return choose % p;
}
// Preconditions: 0 <= k <= min(n,p-1); p > 1 prime
long long choose_mod_two(long long n, long long k, long long p)
{
// reduce n modulo p
n %= p;
// Trivial checks
if (n < k) return 0;
if (k == 0 || k == n) return 1;
// Now 0 < k < n, save a bit of work if k > n/2
if (k > n/2) k = n-k;
// calculate numerator and denominator modulo p
long long num = n, den = 1;
for(n = n-1; k > 1; --n, --k)
{
num = (num * n) % p;
den = (den * k) % p;
}
// Invert denominator modulo p
den = invert_mod(den,p);
return (num * den) % p;
}
To calculate the modular inverse, you can use Fermat's (so-called little) theorem
If p is prime and a not divisible by p, then a^(p-1) ≡ 1 (mod p).
and calculate the inverse as a^(p-2) (mod p), or use a method applicable to a wider range of arguments, the extended Euclidean algorithm or continued fraction expansion, which give you the modular inverse for any pair of coprime (positive) integers:
long long invert_mod(long long k, long long m)
{
if (m == 0) return (k == 1 || k == -1) ? k : 0;
if (m < 0) m = -m;
k %= m;
if (k < 0) k += m;
int neg = 1;
long long p1 = 1, p2 = 0, k1 = k, m1 = m, q, r, temp;
while(k1 > 0) {
q = m1 / k1;
r = m1 % k1;
temp = q*p1 + p2;
p2 = p1;
p1 = temp;
m1 = k1;
k1 = r;
neg = !neg;
}
return neg ? m - p2 : p2;
}
Like calculating a^(p-2) (mod p), this is an O(log p) algorithm, for some inputs it's significantly faster (it's actually O(min(log k, log p)), so for small k and large p, it's considerably faster), for others it's slower.
Overall, this way we need to calculate at most O(log_p k) binomial coefficients modulo p, where each binomial coefficient needs at most O(p) operations, yielding a total complexity of O(p*log_p k) operations.
When k is significantly larger than p, that is much better than the O(k) solution. For k <= p, it reduces to the O(k) solution with some overhead.