Array-syntax vs pointer-syntax and code generation?

Question

In the book, "Understanding and Using C Pointers" by Richard Reese it says on page 85,

int vector[5] = {1, 2, 3, 4, 5};

The code generated by vector[i] is different from the code generated by *(vector+i) . The notation vector[i] generates machine code that starts at location vector , moves i positions from this location, and uses its content. The notation *(vector+i) generates machine code that starts at location vector , adds i to the address, and then uses the contents at that address. While the result is the same, the generated machine code is different. This difference is rarely of significance to most programmers.

You can see the excerpt here. What does this passage mean? In what context would any compiler generate different code for those two? Is there a difference between "move" from base, and "add" to base? I was unable to get this to work on GCC -- generating different machine code.

Matthiew

The case I could think of when it could make any difference is with the use of memory checking tools and code checking tool as they do try to take into account the intended meaning of the code. – Minnieminnnie

"the generated machine code is different." is probably wrong for most contemporary compilers. – Kurman

To me the "adds i to the address" means that is moves i bytes. But what actually happens is that it adds i * sizeof(&vector[0]) bytes. As others have pointed out the C standard declares a[i] as *(a + i) so the passage is just plain confusing. – Highpitched

@KonradRudolph I have lots of questions about pointers from books and published blogs that I think are errata if you want to ruin to your week. https://mcmap.net/q/338911/-for-iterating-though-an-array-should-we-be-using-size_t-or-ptrdiff_t/124486 More in the pipeline too. – Matthiew

The compiler will generate different code if the subscript is a constant expression (such as a[5]) because it can compute the offset at compile time, but I don't see how a[i] and *(a + i) would be handled differently without knowing the value of i at translation time. – Thorman

@JohnBode It should generate the same code if it's a constant expression in *(a + 5). Comparing a[5] with *(a + i) is apples and oranges. – Spontaneous

@Barmar: Some compilers may sometimes benefit from e.g. replacing a[i+5] with (a+5)[i], for a couple of reasons: (1) The compiler can recognize (a+5) as a constant, while ti would be slightly harder to split out the expression i+5 into a constant and non-constant portion. Looking for an indexing expression of the form (const+x) or (x+const) shouldn't be too hard, but would require a bit of extra work. Additionally, if i is unsigned, then a[i+5] must behave predictably with values from UINT_MAX-4 to UINT_MAX, but (a+5)[i] need not do so. – Tenner

@Barmar: "I don't see how a[i] and *(a + i) would be handled differently from each other without knowing the value of i at translation time" - better? I wasn't comparing a[5] to *(a + i). – Thorman

@JohnBode You brought up the issue of the subscript being a constant expression. That point applies equally to both syntaxes. – Spontaneous

Whether compilers in fact will or will not generate different code misses the point. The book asserts that different machine code will be generated because the two syntax alternatives mean different things. It is that justification that is utterly and egregiously wrong. – Liss

Currently this is on HNQ, and I think the title is very ambiguous. I suggest "Array indexing syntax (otherwise it may be array initialization syntax) vs pointer syntax, and assembly (otherwise it may be C) code generation. /// Initially when look at the question I thought it was "I'm writing a C code generation. Should I use int[] a={1,2,3}; or int* a=new int[]{1,2,3};?" or something like that. – Condensed

Answer 1

The quote is just wrong. Pretty tragic that such garbage is still published in this decade. In fact, the C Standard defines x[y] as *(x+y).

The part about lvalues later on the page is completely and utterly wrong too.

IMHO, the best way to use this book is to put it in a recycling bin or burn it.

Ina

As far as I can tell, the paragraph about sizeof is 100% correct. I haven't read page 84, but the part above the heading looks at least somewhat correct. Added together, that's still less than half the page. – Dykes

I didn't mean there was anything wrong with your answer; I was agreeing with your larger point. Less than half the page was reasonable and the rest wasn't just misleading or overly simplified but outright wrong. – Dykes

I wouldn't say it's wrong, but incomplete. The thing is, some compiler might really generate different machine code for x[y] than for *(x+y) (actually, ditto for *(y+x) and y[x]). IOW, if we prefix the whole quote with "On some compilers...", it would actually be right. – Arabic

Also the everyday way is to use this book as a stand for a cup of hot coffee. – Cecilececiley

@Arabic Almost anything is possible if you qualify it with "on some compilers". It could conceivably generate different code depending on the phase of the moon. If the book had said "machine code might be different" it wouldn't be much of an issue. – Spontaneous

If a union contains an array, gcc will generate different machine code for theUnion.anArray[i] and *(theUnion.anArray+i). Only in the former case will gcc be smart enough to recognize that an access to anArray[i] might affect the union and its other members. – Tenner

@Tenner That honestly sounds like a bug on GCC's part, but cool example anyway! – Brazenfaced

@NicHartley: GCC uses a code-generation/execution model that treats an lvalue expressions of the form aggregate.member or aggregate.member[index], or aggregate.member[index1][index2], etc. as operations upon the aggregate, but is unable to recognize a pointer to an aggregate member as having any relation to the aggregate, even in cases where the pointer is used immediately. The Standard treats support for such constructs as a Quality of Implementation issue, and gcc is designed around the fact that the Standard allows low-quality implementations. – Tenner

@NicHartley: See my answer for more info about gcc's behavior. It would be nice to know whether gcc's authors regard the fact that they regard the ability to "flatten" a 2d array using pointer syntax as a design feature or a "missed optimization", and what they would require of code that needs the flattened behavor. – Tenner

@Spontaneous Sure, I just tried to make a minimal change to the original text. To fix it with "might" you would have to change several sentences. But, generating different code here is not the same as relying on the phase of the moon and I can't explain that in a comment, so I tried to explain it in an answer. – Arabic

@srdjan.veljkovic, the book cited by the OP claims that the two syntax variations mean something different, and that therefore different code will be generated. The antecedent of that "therefore" is absolutely, positively wrong. The fact that the asserted consequence may sometimes be realized anyway is pretty much irrelevant. – Liss

@JohnBollinger I actually didn't read the book, only the cited text in the question. It says "different code is generated for different syntax", but, there's no explanation why (is it because of different meanings, or because of the phase of the moon). That's why I think the quote (passage) is not wrong, but, incomplete (which is, essentially, the reason for this question). – Arabic

@DanielH Fair enough; but then it is a curate's egg, and the thing about a partly-bad egg is that it is really not good at all. – Quash

Answer 2

I've got 2 C files: ex1.c

% cat ex1.c
#include <stdio.h>

int main (void) {
    int vector[5] = { 1, 2, 3, 4, 5 };
    printf("%d\n", vector[3]);
}

and ex2.c,

% cat ex2.c
#include <stdio.h>

int main (void) {
    int vector[5] = { 1, 2, 3, 4, 5 };
    printf("%d\n", *(vector + 3));
}

And I compile both into assembly, and show the difference in generated assembly code

% gcc -S ex1.c; gcc -S ex2.c; diff -u ex1.s ex2.s
--- ex1.s       2018-07-17 08:19:25.425826813 +0300
+++ ex2.s       2018-07-17 08:19:25.441826756 +0300
@@ -1,4 +1,4 @@
-       .file   "ex1.c"
+       .file   "ex2.c"
        .text
        .section        .rodata
 .LC0:

Q.E.D.

---

The C standard very explicitly states (C11 n1570 6.5.2.1p2):

2. A postfix expression followed by an expression in square brackets [] is a subscripted designation of an element of an array object. The definition of the subscript operator [] is that E1[E2] is identical to (*((E1)+(E2))). Because of the conversion rules that apply to the binary + operator, if E1 is an array object (equivalently, a pointer to the initial element of an array object) and E2 is an integer, E1[E2] designates the E2-th element of E1 (counting from zero).

---

Additionally, the as-if rule applies here - if the behaviour of the program is the same, the compiler can generate the same code even though the semantics weren't the same.

Bayly

This makes assumptions about a specific compiler and optimizations, but it's generally the same thing I did. I wasn't satisfied, because such a test makes assumptions about a language based on byte code for an architecture. – Matthiew

Interesting note: both according to the quote and in practice, i[vector] also works, although it would be terrible style to do that in most cases. You cannot start at the location i and move vector positions from this location. – Dykes

"I wasn't satisfied, because such a test makes assumptions about a language based on byte code for an architecture" the point is that we are talking about generated assembly, which is as implementation-specific as you can get. The only thing you can do about such a claim - besides noting the equivalency of observable behavior mandated by the standard - is to look at the output of various compilers. – Kwangju

@DanielH - it does work, and IIRC that syntax was featured a few times in the International Obfuscated C Code Contest. (Sometimes in the form 'c'[someptr] or worse.) I have this vague memory of once checking in code that did n["0123456789ABCDEF"] largely to mess with a friend who was doing a code review ... I guess looking back I shouldn't be proud of that ... I only wish I could remember what his reaction was ... – Georgenegeorges

@Georgenegeorges Yep, it does, but the OP’s book’s description would imply it doesn’t. And, you know, you shouldn’t do it anyway. – Dykes

@AnttiHaapala and for the sake of completeness, I just did a similar test using MSVC, and it too generates the exact same code for both forms: movsxd rax,dword ptr [i] mov edx,dword ptr vector[rax * 4] – Giesecke

Answer 3

The cited passage is quite wrong. The expressions vector[i] and *(vector+i) are perfectly identical and can be expected to generate identical code under all circumstances.

The expressions vector[i] and *(vector+i) are identical by definition. This is a central and fundamental property of the C programming language. Any competent C programmer understands this. Any author of a book entitled Understand and Using C Pointers must understand this. Any author of a C compiler will understand this. The two fragments will generate identical code not by accident, but because virtually any C compiler will, in effect, translate one form into the other almost immediately, such that by the time it gets to its code generation phase, it won't even know which form had been used initially. (I would be pretty surprised if a C compiler ever generated significantly different code for vector[i] as opposed to *(vector+i).)

And in fact, the cited text contradicts itself. As you noted, the two passages

The notation vector[i] generates machine code that starts at location vector , moves i positions from this location, and uses its content.

and

The notation *(vector+i) generates machine code that starts at location vector, adds i to the address, and then uses the contents at that address.

say basically the same thing.

His language is eerily similar to that in question 6.2 of the old C FAQ list:

...when the compiler sees the expression a[3], it emits code to start at the location "a", move three past it, and fetch the character there. When it sees the expression p[3], it emits code to start at the location "p", fetch the pointer value there, add three to the pointer, and finally fetch the character pointed to.

But of course the key difference here is that a is an array and p is a pointer. The FAQ list is talking not about a[3] versus *(a+3), but rather about a[3] (or *(a+3)) where a is an array, versus p[3] (or *(p+3)) where p is a pointer. (Of course those two cases generate different code, because arrays and pointers are different. As the FAQ list explains, fetching an address from a pointer variable is fundamentally different from using the address of an array.)

Paramorph

You mention the old C FAQ, that's a really good find. But you don't tal about why they're different even in that context: you just say (Of course those two cases generate different code, because arrays and pointers are different.) perhaps some explaining would be good. – Matthiew

The Standard may treat the expressions as equivalent, but many compilers merely interpret that as suggesting that in the cases where the Standard would define the behavior of one, it defines the behavior of both. The Standard doesn't impose any requirements on the behavior of accessing elements of non-character arrays within unions (or, for that matter, any non-character union members) but such arrays would be rather useless if they didn't exhibit type-punning behavior like other members . GCC will process someUnion.array[i] that way, but does not do so for *(someUnion.arr+i). – Tenner

"are perfectly identical and can be expected to generate identical code under all circumstances" - That's not what the standard says. The definition is about semantics, so in both cases you will definitely end up with the same array contents. How this is achieved is up to the compiler and can be quite different from compiler to compiler, platform to platform and between optimization levels. – Kurman

Answer 4

I think what the original text may be referring to is some optimizations which some compiler may or may not perform.

Example:

for ( int i = 0; i < 5; i++ ) {
  vector[i] = something;
}

vs.

for ( int i = 0; i < 5; i++ ) {
  *(vector+i) = something;
}

In the first case, an optimizing compiler may detect that the array vector is iterated over element by element and thus generate something like

void* tempPtr = vector;
for ( int i = 0; i < 5; i++ ) {
  *((int*)tempPtr) = something;
  tempPtr += sizeof(int); // _move_ the pointer; simple addition of a constant.
}

It might even be able to use the target CPU's pointer post-increment instructions where available.

For the second case, it is "harder" for the compiler to see that the address that's calculated via some "arbitrary" pointer arithmetics expression shows the same property of monotonically advancing a fixed amount in each iteration. It might thus not find the optimization and calculate ((void*)vector+i*sizeof(int)) in each iteration which uses an additional multiplication. In this case there's no (temporary) pointer that gets "moved" but only a temporary address re-calculated.

However, the statement probably does not universally hold for all C compilers in all versions.

Update:

I checked the above example. It appears that without optimizations enabled at least gcc-8.1 x86-64 generates more code (2 extra instructions) for the second (pointer-arithmethics) form than the first (array index).

See: https://godbolt.org/g/7DaPHG

However, with any optimizations turned on (-O...-O3) the generated code is the same (length) for both.

Kurman

No. The as-if rule applies. If the optimizer is smart enough it can generate the same code. In the above example most compilers are since a[i] is simply parsed into the same pre-optimized data as *(a+i). – Highpitched

@GoswinvonBrederlow "If the optimizer is smart enough it can generate the same code. In the above example most compilers are" - That's basically what I was trying to say :) – Kurman

Answer 5

The Standard specifies the behavior of arr[i] when arr is an array object as being equivalent to decomposing arr to a pointer, adding i, and dereferencing the result. Although the behaviors would be equivalent in all Standard-defined cases, there are some cases where compilers process actions usefully even though the Standard does require it, and the handling of arrayLvalue[i] and *(arrayLvalue+i) may differ as a consequence.

For example, given

char arr[5][5];
union { unsigned short h[4]; unsigned int w[2]; } u;

int atest1(int i, int j)
{
if (arr[1][i])
    arr[0][j]++;
return arr[1][i];
}
int atest2(int i, int j)
{
if (*(arr[1]+i))
    *((arr[0])+j)+=1;
return *(arr[1]+i);
}
int utest1(int i, int j)
{
    if (u.h[i])
        u.w[j]=1;
    return u.h[i];
}
int utest2(int i, int j)
{
    if (*(u.h+i))
        *(u.w+j)=1;
    return *(u.h+i);
}

GCC's generated code for test1 will assume that arr[1][i] and arr[0][j] cannot alias, but the generated code for test2 will allow for pointer arithmetic to access the entire array, On the flip side, gcc will recognize that in utest1, lvalue expressions u.h[i] and u.w[j] both access the same union, but it's not sophisticated enough to notice the same about *(u.h+i) and *(u.w+j) in utest2.

Tenner

Answer 6

Let me try to answer this "in the narrow" (others have already described why the description "as-is" is somewhat lacking/incomplete/misleading):

In what context would any compiler generate different code for those two?

A "not-very-optimizing" compiler might generate different code in just about any context, because, while parsing, there's a difference: x[y] is one expression (index into an array), while *(x+y) are two expressions (add an integer to a pointer, then dereference it). Sure, it's not very hard to recognize this (even while parsing) and treat it the same, but, if you're writing a simple/fast compiler, then you avoid putting "too much smarts into it". As an example:

char vector[] = ...;
char f(int i) {
    return vector[i];
}
char g(int i) {
    return *(vector + i);
}

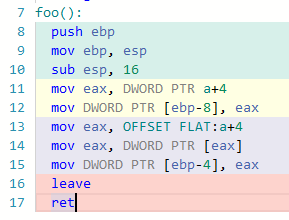
Compiler, while parsing f(), sees the "indexing" and may generate something like (for some 68000-like CPU):

MOVE D0, [A0 + D1] ; A0/vector, D1/i, D0/result of function

OTOH, for g(), compiler sees two things: first a dereference (of "something yet to come") and then the adding of integer to pointer/array, so being not-very-optimizing, it could end up with:

MOVE A1, A0   ; A1/t = A0/vector
ADD A1, D1    ; t += i/D1
MOVE D0, [A1] ; D0/result = *t

Obviously, this is very implementation dependent, some compiler might also dislike using complex instructions as used for f() (using complex instructions makes it harder to debug the compiler), the CPU might not have such complex instructions, etc.

Is there a difference between "move" from base, and "add" to base?

The description in the book is arguably not well-worded. But, I think the author wanted to describe the distinction shown above - indexing ("move" from base) is one expression, while "add and then dereference" are two expressions.

This is about compiler implementation, not language definition, the distinction which should have also been explicitly indicated in the book.

Arabic

Answer 7

I tested the Code for some compiler variations, most of them give me the same assembly code for both instructions (tested for x86 with no optimization). Interesting is, that the gcc 4.4.7 does exactly, what you mentioned: Example:

Other langauges like ARM or MIPS are doing sometimes the same, but I didn`t tested it all. So it seems their was a difference, but later versions of gcc "fixed" this bug.

Franciscka

And did you try optimizations? – Errand

no, sorry the examples are to trivial, everything would be optimized out. If you like, you can try it at Compiler Explorer – Franciscka

Declare the array as volatile and the code will not be optimized away. – Kurman

with -O>1 assembler output is for both: ` mov eax, DWORD PTR vector[rip+4]` – Franciscka

Answer 8

This is a sample array syntax as used in C.

int a[10] = {1,2,3,4,5,6,7,8,9,10};

By