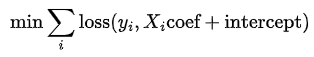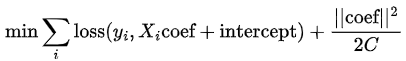What is the inverse of regularization strength in Logistic Regression? How should it affect my code?

Question

I am using sklearn.linear_model.LogisticRegression in scikit learn to run a Logistic Regression.

C : float, optional (default=1.0) Inverse of regularization strength;
    must be a positive float. Like in support vector machines, smaller
    values specify stronger regularization.

What does C mean here in simple terms? What is regularization strength?

Complexioned

Did you ask Google? I did. This link was the first one – Caramelize

@RichardScriven I did, and found it very complicated and hoped someone would be kind enough to break it down to simple English for me! Thanks for the link :) – Complexioned

No problem. Although it looks more like difficult mathematics than simple english. :) – Caramelize

I asked Google, this was the first link to come up ;) – Inexplicable

I asked quora, this was the link in the first answer ;) – Reopen

Answer 1

Regularization is applying a penalty to increasing the magnitude of parameter values in order to reduce overfitting. When you train a model such as a logistic regression model, you are choosing parameters that give you the best fit to the data. This means minimizing the error between what the model predicts for your dependent variable given your data compared to what your dependent variable actually is.

The problem comes when you have a lot of parameters (a lot of independent variables) but not too much data. In this case, the model will often tailor the parameter values to idiosyncrasies in your data -- which means it fits your data almost perfectly. However because those idiosyncrasies don't appear in future data you see, your model predicts poorly.

To solve this, as well as minimizing the error as already discussed, you add to what is minimized and also minimize a function that penalizes large values of the parameters. Most often the function is λΣθ_j², which is some constant λ times the sum of the squared parameter values θ_j². The larger λ is the less likely it is that the parameters will be increased in magnitude simply to adjust for small perturbations in the data. In your case however, rather than specifying λ, you specify C=1/λ.

Optative

To the best of my knowledge, the penalization is applied to decrease the magnitude of the parameters. – Haversack

@ArtonDorneles yes there is a penalty for increasing the magnitude of the parameters. Conversely, there tends to be a benefit to decreasing the magnitude of the parameters. – Optative

I was just reading about L1 and L2 regularization, this link was helpful: LINK. So now I know that the term you mention here is L2 regularization. – Bonnette

Yes, this term is L2 regularization, and to catch everyone else up, L2 just means $\lambda \sum \theta_{j}^{2}$, whereas L1 just means $\lambda \sum \abs{\theta_{j}}$. It's that simply, but the impact is significant because L1 tends towards sparsity (fewer feature parameters in the model) since $x^2$ becomes an insignificant addition to the penalty far more quickly than $x$ as $x < 1$. – Simplify

Jeez! I thought that SO comments allowed for latex math... I hope y'all can make sense of what I wrote. – Simplify

Where and how the "C" parameter is used in the sklearn source pls? – Overtrade

I think this answer explains the regularization well and intuitively but it should also add the explanation of why C=1/λ in logistic regression :-( – Perforation

Answer 2

In one sentence, regularization makes the model perform worse on training data so that it may perform better on holdout data.

Logistic regression is an optimization problem where the following objective function is minimized.

where loss function looks like (at least for solver='lbfgs') the following.

Regularization adds a norm of the coefficients to this function. The following implements the L2 penalty.

From the equation, it's clear that the regularization term is there to penalize large coefficients (the minimization problem is solving for the coefficients that minimize the objective function). Since the size of each coefficient depends on the scale of its corresponding variable, scaling the data is required so that the regularization penalizes each variable equally. The regularization strength is determined by C and as C increases, the regularization term becomes smaller (and for extremely large C values, it's as if there is no regularization at all).

If the initial model is overfit (as in, it fits the training data too well), then adding a strong regularization term (with small C value) makes the model perform worse for the training data, but introducing such "noise" improves the model's performance on unseen (or test) data.

---

An example with 1000 samples and 200 features shown below. As can be seen from the plot of accuracy over different values of C, if C is large (with very little regularization), there is a big gap between how the model performs on training data and test data. However, as C decreases, the model performs worse on training data but performs better on test data (test accuracy increases). However, when C becomes too small (or the regularization becomes too strong), the model begins performing worse again because now the regularization term completely dominates the objective function.

---

Code used to to produce the graph:

import pandas as pd
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression

# make sample data
X, y = make_classification(1000, 200, n_informative=195, random_state=2023)
# split into train-test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2023)

# normalize the data
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

# train Logistic Regression models for different values of C
# and collect train and test accuracies
scores = {}
for C in (10**k for k in range(-6, 6)):
    lr = LogisticRegression(C=C)
    lr.fit(X_train, y_train)
    scores[C] = {'train accuracy': lr.score(X_train, y_train), 
                 'test accuracy': lr.score(X_test, y_test)}

# plot the accuracy scores for different values of C
pd.DataFrame.from_dict(scores, 'index').plot(logx=True, xlabel='C', ylabel='accuracy');

Noble