Design an efficient algorithm to sort 5 distinct - very large - keys less than 8 comparisons in the worst case. You can't use radix sort.
Design an efficient algorithm to sort 5 distinct keys in fewer than 8 comparisons
If this is homework, and it sounds like it, please tell us what you have done and where you are stuck. –
Photoluminescence
it s not a homework question. Yes i m taking algorithm class but it s just a question i m curious. I asked a similar question before I was curious if there s a better worst case. –
Gahan
I find the median in 6 comparisons and i did two more comparisons, which is 8 again. I m curious if there s a better solution to this. –
Gahan
I m sure 8 is the worst case, using merge sort. –
Gahan
quicksort is also 8. Cant use insertion sort, selection sort, heapsort, bubble sort, and the linear time sorting algorithms, such as radix sort. –
Gahan
The information-theoretical minimum is 7 comparisons (you have 2^7=128 possible outputs from asking 7 boolean questions, and there are 120 permutations of 5 numbers). That doesn't mean it's possible though. –
Dichlamydeous
There is an answer to it, which i dont know that s why i asked :) –
Gahan
This is weird, I could swear that we had this exact same question 2-3 weeks ago... –
Ignition
:) That was a median question. Finding the median of 5 keys which can be done with 6 comparisons, and which there was no correct answers. –
Gahan
"very large" means no hash-like sort? If not, you can sort this keys putting each one into a corresponding location of an array, then reading it from the beginning –
Unattached
:) very large means, you cant use linear time sorting, like counting sort, radix sort, bucket sort. –
Gahan
If you cannot sort, you can unroll the comparisons giving essentially all 120 possibilities in a LOT of nested ifs. –
Lys
The best algorithm known was first published by H.B. Demuth in 1956, and can be found in chapter 5.3.1 of volume 3 of The Art of Computer Programming, by Donald Knuth. –
Aker
Compare A to B and C to D. WLOG, suppose A>B and C>D. Compare A to C. WLOG, suppose A>C. Sort E into A-C-D. This can be done with two comparisons. Sort B into {E,C,D}. This can be done with two comparisons, for a total of seven.
(a,b=> 1), (c,d=>1), (a,c=>1),(e, (a,c,d) => can be 3), (b, (e,c,d)=> can also be 3) Am i missing a point? –
Gahan
@unknown, to sort E into A-C-D, first compare E to C. Then if E>C compare E to A, otherwise compare E to D. Sorting B into {E,C,D} is the same. –
Stork
This is known as Ford-Johnson algorithm aka merge insertion. This is the link for the related paper published in 1959. If you have trouble accessing the link, please search for "The tournament problem". –
Desmoid
This is pseudocode based on Beta's answer. Might have some mistakes as I did this in a hurry.
if (A > B)
swap A, B
if (C > D)
swap C, D
if (A > C)
swap A, C
swap B, D # Thanks Deqing!
if (E > C)
if (E > D) # A C D E
if (B > D)
if (B > E)
return (A, C, D, E, B)
else
return (A, C, D, B, E)
else
if (B < C)
return (A, B, C, D, E)
else
return (A, C, B, D, E)
else # A C E D
if (B > E)
if (B > D)
return (A, C, E, D, B)
else
return (A, C, E, B, D)
else
if (B < C)
return (A, B, C, E, D)
else
return (A, C, B, E, D)
else
if (E < A) # E A C D
if (B > C)
if (B > D)
return (E, A, C, D, B)
else
return (E, A, C, B, D)
else
return (E, A, B, C, D)
else # A E C D
if (B > C)
if (B > D)
return (A, E, C, D, B)
else
return (A, E, C, B, D)
else
if (B < E)
return (A, B, E, C, D)
else
return (A, E, B, C, D)
i wish i could pick two right answers :) Thanks for the effort though. Appreciated. –
Gahan
I don't understand, how the first 3 comparison gets
A-C-D? E.g. for ABCD as 9,10,1,2 the first 3 comparison get A,C,D as 1-9-2, not we expected. I guess the 3rd comparison should be swap A, C; swap B, D; –
Frediafredie Well spotted! If (A > C) then A may also be greater than D, but we can't be sure without a comparison. But swapping (A,B) with (C,D) solves the problem; afterwards we know A>B, A>C, and C>D. Edited my answer. –
Panic
this might fail for 1 1 2 2 1 –
Felike
I have tested it and it works correctly for 1 1 2 2 1, returning 1 1 1 2 2. –
Panic
Yeah rewrote this into C++ and it worked fine tested it in Debug/Release x64/x86 and yeah performed solid. I had a more simplified version that was 7 or 8 ifs but did less swapping of values but both come to about same speed in release mode with this being faster in x86 and slower in x64 for me but by so little it doesn't matter given i was doing 70mil sorts. Here's your pseudo code in C++ pastebin.com/raw/BqZQsJPN pastebins formatting made it a little weird btw. –
Oocyte
It has to be 7 or more comparisons.
There are 120 (5 factorial) ways for 5 objects to be arranged. An algorithm using 6 comparisons can only tell apart 2^6 = 64 different initial arrangements, so algorithms using 6 or less comparisons cannot sort all possible inputs.
There may be a way to sort using only 7 comparisons. If you only want to sort 5 elements, such an algorithm could be found (or proved not to exist) by brute force.
Nice answer too, I already commented that I know It can be found with 7 Comparisons, but dont know how :) –
Gahan
Five items can be sorted with at most seven comparisons, because log2(5!) = 6.9. I suggest checking if any standard sorting algorithm achieves this number. If not, it should be quite easy to hard-code a comparison sequence because of the low number of required comparisons.
I suggest using this algorithm to find the comparison sequence:
- Create a list with all 120 permutations of
[1..5]. - Try all (initially
5 * 4 = 20) possible comparisons and choose the one which splits the list into two most equally sized lists. - Apply this split, then:
- if the two splits contain only one element, terminate
- otherwise, go to 2.
I wrote a small program to do this, and here is the result:
Comparison 1: 0-1 [60|60] // First comparison item 0 with item 1, splits case 60/60
Comparison 2: 2-3 [30|30] // Second comparison for the first half of the first comparison
Comparison 3: 0-2 [15|15] // Third comparison for the first half of the second comparison for the first half of first comparison
Comparison 4: 2-4 [8|7]
Comparison 5: 3-4 [4|4]
Comparison 6: 1-3 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 6: 1-4 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 5: 0-4 [4|3]
Comparison 6: 1-2 [2|2]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 6: 1-2 [1|2]
Comparison 7: 1-3 [1|1]
Comparison 4: 0-4 [8|7]
Comparison 5: 1-4 [4|4]
Comparison 6: 1-3 [2|2]
Comparison 7: 3-4 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 6: 3-4 [2|2]
Comparison 7: 0-3 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 5: 0-3 [4|3]
Comparison 6: 1-3 [2|2]
Comparison 7: 2-4 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 6: 2-4 [2|1]
Comparison 7: 3-4 [1|1]
Comparison 3: 0-3 [15|15] // Third comparison for the second half of the second comparison for the first half of first comparison
Comparison 4: 3-4 [8|7]
Comparison 5: 2-4 [4|4]
Comparison 6: 1-2 [2|2]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 6: 1-4 [2|2]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 5: 0-4 [4|3]
Comparison 6: 1-3 [2|2]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 6: 1-2 [2|1]
Comparison 7: 1-3 [1|1]
Comparison 4: 0-4 [8|7]
Comparison 5: 1-4 [4|4]
Comparison 6: 1-2 [2|2]
Comparison 7: 2-4 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 6: 2-4 [2|2]
Comparison 7: 0-2 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 5: 0-2 [4|3]
Comparison 6: 1-2 [2|2]
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 6: 2-4 [1|2]
Comparison 7: 3-4 [1|1]
Comparison 2: 2-3 [30|30] // Second comparison for the second half of the first comparison
Comparison 3: 0-3 [15|15]
Comparison 4: 0-4 [7|8]
Comparison 5: 0-2 [3|4]
Comparison 6: 2-4 [2|1]
Comparison 7: 3-4 [1|1]
Comparison 6: 1-2 [2|2]
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 5: 1-4 [4|4]
Comparison 6: 2-4 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 6: 1-2 [2|2]
Comparison 7: 0-2 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 4: 3-4 [7|8]
Comparison 5: 0-4 [3|4]
Comparison 6: 1-2 [1|2]
Comparison 7: 1-3 [1|1]
Comparison 6: 1-3 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 5: 2-4 [4|4]
Comparison 6: 1-4 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 6: 1-2 [2|2]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 3: 0-2 [15|15]
Comparison 4: 0-4 [7|8]
Comparison 5: 0-3 [3|4]
Comparison 6: 2-4 [1|2]
Comparison 7: 3-4 [1|1]
Comparison 6: 1-3 [2|2]
Comparison 7: 2-4 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 5: 1-4 [4|4]
Comparison 6: 3-4 [2|2]
Comparison 7: 1-3 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 6: 1-3 [2|2]
Comparison 7: 0-3 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 4: 2-4 [7|8]
Comparison 5: 0-4 [3|4]
Comparison 6: 1-2 [2|1]
Comparison 7: 1-3 [1|1]
Comparison 6: 1-2 [2|2]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 5: 3-4 [4|4]
Comparison 6: 1-4 [2|2]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 6: 1-3 [2|2]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
But now the question is how to implement this in an efficient way. Maybe one could use a look-up table to store the comparison sequence. I am also not sure how to derive the ordered output from this comparison sequence in an efficient way.
Sorting the result from above by the comparison reveals an obvious structure for the first comparisons, but it becomes harder with an increasing amount of comparisons. All blocks are symmetric around the middle, indicated by -----.
Comparison 1: 0-1 [60|60]
Comparison 2: 2-3 [30|30]
Comparison 2: 2-3 [30|30]
Comparison 3: 0-2 [15|15]
Comparison 3: 0-3 [15|15]
-----
Comparison 3: 0-3 [15|15]
Comparison 3: 0-2 [15|15]
Comparison 4: 2-4 [8|7]
Comparison 4: 0-4 [8|7]
Comparison 4: 3-4 [8|7]
Comparison 4: 0-4 [8|7]
-----
Comparison 4: 0-4 [7|8]
Comparison 4: 3-4 [7|8]
Comparison 4: 0-4 [7|8]
Comparison 4: 2-4 [7|8]
Comparison 5: 3-4 [4|4]
Comparison 5: 0-4 [4|3]
Comparison 5: 1-4 [4|4]
Comparison 5: 0-3 [4|3]
Comparison 5: 2-4 [4|4]
Comparison 5: 0-4 [4|3]
Comparison 5: 1-4 [4|4]
Comparison 5: 0-2 [4|3]
-----
Comparison 5: 0-2 [3|4]
Comparison 5: 1-4 [4|4]
Comparison 5: 0-4 [3|4]
Comparison 5: 2-4 [4|4]
Comparison 5: 0-3 [3|4]
Comparison 5: 1-4 [4|4]
Comparison 5: 0-4 [3|4]
Comparison 5: 3-4 [4|4]
Comparison 6: 1-3 [2|2]
Comparison 6: 1-4 [2|2]
Comparison 6: 1-2 [2|2]
Comparison 6: 1-2 [1|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 3-4 [2|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 2-4 [2|1]
Comparison 6: 1-2 [2|2]
Comparison 6: 1-4 [2|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 1-2 [2|1]
Comparison 6: 1-2 [2|2]
Comparison 6: 2-4 [2|2]
Comparison 6: 1-2 [2|2]
Comparison 6: 2-4 [1|2]
-----
Comparison 6: 2-4 [2|1]
Comparison 6: 1-2 [2|2]
Comparison 6: 2-4 [2|2]
Comparison 6: 1-2 [2|2]
Comparison 6: 1-2 [1|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 1-2 [2|2]
Comparison 6: 1-4 [2|2]
Comparison 6: 2-4 [1|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 3-4 [2|2]
Comparison 6: 1-3 [2|2]
Comparison 6: 1-2 [2|1]
Comparison 6: 1-2 [2|2]
Comparison 6: 1-4 [2|2]
Comparison 6: 1-3 [2|2]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
-----
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 7: 0-2 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 2-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 7: 0-3 [1|1]
Comparison 7: 3-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-3 [1|1]
Comparison 7: 1-2 [1|1]
Comparison 7: 1-4 [1|1]
Comparison 7: 1-2 [1|1]
Nice answer, I know that. Using comparison tree. There are 5! possible answer which is log120. But which algorithm to find this route? –
Gahan
FWIW, here's a compact and easy to follow Python version with tests to make sure it works:
def sort5(a, b, c, d, e):
'Sort 5 values with 7 Comparisons'
if a < b: a, b = b, a
if c < d: c, d = d, c
if a < c: a, b, c, d = c, d, a, b
if e < c:
if e < d: pass
else: d, e = e, d
else:
if e < a: c, d, e = e, c, d
else: a, c, d, e = e, a, c, d
if b < d:
if b < e: return b, e, d, c, a
else: return e, b, d, c, a
else:
if b < c: return e, d, b, c, a
else: return e, d, c, b, a
if __name__ == '__main__':
from itertools import permutations
assert all(list(sort5(*p)) == sorted(p) for p in permutations(range(5)))
According to Wikipedia:
Determining the exact number of comparisons needed to sort a given number of entries is a computationally hard problem even for small n, and no simple formula for the solution is known."
Presumably this means there is no known tractable (efficient) algorithm for determining an exactly optimal comparison sort.
He doesn't need a formula, just the answer for n=5. The quote says that it's a hard problem even for small n, but it doesn't mean that small. There's a hard lower limit of 7 on the worst case, and a known solution that gets it in 7 at worst. Who cares how hard it is for n=6? –
Particiaparticipant
Sorting networks
have a restricted structure,
so don't answer the original question; but they're fun.
List of Sorting Networks
generates nice diagrams or lists of SWAPs for up to 32 inputs.
For 5, it gives
There are 9 comparators in this network, grouped into 6 parallel operations.
[[0,1],[3,4]]
[[2,4]]
[[2,3],[1,4]]
[[0,3]]
[[0,2],[1,3]]
[[1,2]]
I have written a C implementation of the solution to this problem which can be found here: Sorting 5 elements using 7 comparisons
My code is well commented with an explanation of why it is working.
Sample sequence of operations, using mergesort (the merge function below will merge two sorted sublists into a single sorted combined list):
elements[1..2] <- merge(elements[1..1], elements[2..2]) # 1 comparison
elements[3..4] <- merge(elements[3..3], elements[4..4]) # 1 comparison
elements[3..5] <- merge(elements[3..4], elements[5..5]) # 1-2 comparisons
elements[1..5] <- merge(elements[1..2], elements[3..5]) # 2-4 comparisons
A B C D E
A
| C D E - 1 Comparison
B
A C
| | E - 1 Comparison
B D
A
/ \
B C E - 1 Comparison
\
D
E needs 3 comparisons. It should be compared to A, C, D
Try A-C-D-E in that order.
Overall there will be nine comparisons -- not very performant.
Huh?! Who posts a screenshot of their Word document on a programming site? –
Batchelder
Ben. What s the big deal ? How am i supposed to draw that using SO thingies. –
Gahan
I actually like this. Change of scenery is not bad every once in a while. –
Spadework
Use the <pre> tags to get fixed-width text without formatting. –
Panic
Fixed it for you. If you click 'edit', you'll be able to see what I did. Please refrain from using images in the future -- they aren't searchable, and they're dependent upon whatever you're saving the image to always being available. –
Elisabeth
Others have stated that there are 5! = 120 arrangements (permutations) to handle, so you need 7 comparisons. To identify the permutation, in principle, you can construct a big nested if statement 7 comparisons deep. Having identified the permutation, a precalculated swap/rotation sequence can be applied.
The first problem is that the choice of second comparison depends on the result of the first comparison and so on. The trick at each stage is to choose a good comparison to divide the current set of possible permutations into two equal subsets. Simplest approach - evaluate the split that each comparison would achieve until you find a suitably balanced one. Exit early if you find a perfect balance, but be aware that perfect balance won't always be possible as we don't have exactly 2^7=128 permutations - in some (I assume 8) cases, we only need six comparisons.
The second problem is designing the swap/rotation sequences for each of the 120 possible permutations, and that's probably a dynamic programming thing. Probably requires recursive search of an if-I-do-this, the next result is that, then recurse "game tree", and you should really cache intermediate results IOW. Too tired to figure out the details ATM, sorry.
You might put all the steps into a digraph that fans out (identifying the permutation), then fans back in (applying each reordering step). Then, probably run it through a digraph minimisation algorithm.
Wrap this up in a code generator and you're done - your own algorithmically near-perfect 5 item sorter. The digraph stuff kind of implies gotos in the generated code (esp. if you minimise), but people tend to turn a blind eye to that in generated code.
Of course all this is a bit brute force, but why bother with elegance and efficiency - odds are you'll only run the working generator once anyway, and the problem size is small enough to be achievable (though probably not if you do independent naive "game tree" searches for each permutation).
Here is C++ implementation which sorts 5 elements in <= 7 comparisons. Was able to find 8 cases which can be sorted in 6 comparisons. That makes sense if we imagine full binary tree with 120 leaf nodes, there will be 112 nodes at level 7 and 8 leaf nodes at level 6. Here is the full code that is tested to work for all possible permutations.
#include <vector>
#include <iostream>
#include <algorithm>
#include <string>
#include <cstdlib>
#include <cmath>
#include <cassert>
#include <numeric>
using namespace std;
ostream& operator << ( ostream& os, vector<int> v )
{
cout << "[ ";
for ( auto x: v ) cout << x << ' ';
cout << "]";
return os;
}
class Comp {
int count;
public:
Comp(): count{0}{}
bool isLess( vector<int> v, int i, int j ) {
count++;
//cout << v << "Comparison#" << count << ": " << i << ", " << j << endl;
return v[ i ] < v[ j ];
}
int getCount() { return count; }
};
int mySort( vector<int> &v )
{
Comp c;
if ( c.isLess( v, 1, 0 ) ) {
swap( v[ 0 ], v[ 1 ] );
}
if ( c.isLess( v, 3, 2 ) ) {
swap( v[ 2 ], v[ 3 ] );
}
// By now (0, 1) (2, 3) (4)
if ( c.isLess( v, 0, 2 ) ) {
// ( 0, 2, 3 ) (1)
swap( v[ 1 ], v[ 2 ] );
swap( v[ 2 ], v[ 3 ] );
} else {
// ( 2, 0, 1 ) ( 3 )
swap( v[ 1 ], v[ 2 ] );
swap( v[ 0 ], v[ 1 ] );
}
// By now sorted order ( 0, 1, 2 ) ( 3 ) ( 4 ) and know that 3 > 0
if ( c.isLess( v, 4, 1 ) ) {
if ( c.isLess( v, 4, 0 ) ) {
// ( 4, 0, 1, 2 ) ( 3 ) ( ... )
v.insert( v.begin(), v[4] );
// By now ( 0, 1, 2, 3 ) ( 4 ) ( ... ) and know that 4 > 1
if ( c.isLess( v, 4, 2 ) ) {
// ( 0, 1, 4, 2, 3 ) ( ... )
v.insert( v.begin() + 2, v[4] );
} else {
if ( c.isLess( v, 4, 3 ) ) {
// ( 0, 1, 2, 4, 3 ) ( ... )
v.insert( v.begin() + 3, v[4] );
} else {
// ( 0, 1, 2, 3, 4 ) ( ... )
v.insert( v.begin() + 4, v[4] );
}
}
// ( 1 2 3 4 5 ) and trim the rest
v.erase( v.begin()+5, v.end() );
return c.getCount(); /////////// <--- Special case we could been done in 6 comparisons
} else {
// ( 0, 4, 1, 2 ) ( 3 ) ( ... )
v.insert( v.begin() + 1, v[4] );
}
} else {
if ( c.isLess( v, 4, 2 ) ) {
// ( 0, 1, 4, 2 ) ( 3 ) ( ... )
v.insert( v.begin() + 2, v[4] );
} else {
// ( 0, 1, 2, 4 ) ( 3 ) ( ... )
v.insert( v.begin() + 3, v[4] );
}
}
// By now ( 0, 1, 2, 3 ) ( 4 )( ... ): with 4 > 0
if ( c.isLess( v, 4, 2 ) ) {
if ( c.isLess( v, 4, 1 ) ) {
// ( 0, 4, 1, 2, 3 )( ... )
v.insert( v.begin() + 1, v[4] );
} else {
// ( 0, 1, 4, 2, 3 )( ... )
v.insert( v.begin() + 2, v[4] );
}
} else {
if ( c.isLess( v, 4, 3 ) ) {
// ( 0, 1, 2, 4, 3 )( ... )
v.insert( v.begin() + 3, v[4] );
} else {
// ( 0, 1, 2, 3, 4 )( ... )
v.insert( v.begin() + 4, v[4] );
}
}
v.erase( v.begin()+5, v.end() );
return c.getCount();
}
#define TEST_ALL
//#define TEST_ONE
int main()
{
#ifdef TEST_ALL
vector<int> v1(5);
iota( v1.begin(), v1.end(), 1 );
do {
vector<int> v2 = v1, v3 = v1;
int count = mySort( v2 );
if ( count == 6 )
cout << v3 << " => " << v2 << " #" << count << endl;
} while( next_permutation( v1.begin(), v1.end() ) );
#endif
#ifdef TEST_ONE
vector<int> v{ 1, 2, 3, 1, 2};
mySort( v );
cout << v << endl;
#endif
}
For sorting networks, it is not possible to have less than 9 comparisons to sort 5 items when the input is not known. The lower bound has been proven for sorting networks up to 10. See https://en.wikipedia.org/wiki/Sorting_network.
Correctness of sorting networks could be verified by the Zero-one principle as mentioned in The Art of Computer Programming, Vol 3 by Knuth. That is, if a sorting network can correctly sort all permutations of 0s and 1s, then it is a correct sorting network. None of the algorithms mentioned on this post passed the Zero-one test.
In addition, the lower bound says that comparison based sorts cannot have less than ceil(log(n!)) comparators to correctly sort, however, it does not mean that this is achievable.
(See caveat introducing denis answer.) –
Jadejaded
This Python function sorts any input of 5 items in 6 or 7 comparisons (8 permutations need just 6 comparisons, while the remaining 112 permutations require 7):
def sort_5_items(a, b, c, d, e):
n_comparisons = 0
def lt(value_1, value_2):
nonlocal n_comparisons
n_comparisons += 1
return value_1 < value_2
if lt(a, b):
if lt(c, d):
if lt(a, c):
if lt(c, e):
if lt(d, e):
if lt(b, d):
if lt(b, c):
return (a, b, c, d, e), n_comparisons
return (a, c, b, d, e), n_comparisons
if lt(b, e):
return (a, c, d, b, e), n_comparisons
return (a, c, d, e, b), n_comparisons
if lt(b, e):
if lt(b, c):
return (a, b, c, e, d), n_comparisons
return (a, c, b, e, d), n_comparisons
if lt(b, d):
return (a, c, e, b, d), n_comparisons
return (a, c, e, d, b), n_comparisons
if lt(a, e):
if lt(b, c):
if lt(b, e):
return (a, b, e, c, d), n_comparisons
return (a, e, b, c, d), n_comparisons
if lt(b, d):
return (a, e, c, b, d), n_comparisons
return (a, e, c, d, b), n_comparisons
if lt(b, c):
return (e, a, b, c, d), n_comparisons
if lt(b, d):
return (e, a, c, b, d), n_comparisons
return (e, a, c, d, b), n_comparisons
if lt(a, e):
if lt(b, e):
if lt(b, d):
if lt(d, e):
return (c, a, b, d, e), n_comparisons
return (c, a, b, e, d), n_comparisons
if lt(a, d):
return (c, a, d, b, e), n_comparisons
return (c, d, a, b, e), n_comparisons
if lt(d, e):
if lt(a, d):
return (c, a, d, e, b), n_comparisons
return (c, d, a, e, b), n_comparisons
if lt(b, d):
return (c, a, e, b, d), n_comparisons
return (c, a, e, d, b), n_comparisons
if lt(a, d):
if lt(b, d):
if lt(c, e):
return (c, e, a, b, d), n_comparisons
return (e, c, a, b, d), n_comparisons
if lt(c, e):
return (c, e, a, d, b), n_comparisons
return (e, c, a, d, b), n_comparisons
if lt(c, e):
if lt(d, e):
return (c, d, e, a, b), n_comparisons
return (c, e, d, a, b), n_comparisons
return (e, c, d, a, b), n_comparisons
if lt(a, d):
if lt(d, e):
if lt(c, e):
if lt(b, c):
if lt(b, d):
return (a, b, d, c, e), n_comparisons
return (a, d, b, c, e), n_comparisons
if lt(b, e):
return (a, d, c, b, e), n_comparisons
return (a, d, c, e, b), n_comparisons
if lt(b, e):
if lt(b, d):
return (a, b, d, e, c), n_comparisons
return (a, d, b, e, c), n_comparisons
if lt(b, c):
return (a, d, e, b, c), n_comparisons
return (a, d, e, c, b), n_comparisons
if lt(a, e):
if lt(b, d):
if lt(b, e):
return (a, b, e, d, c), n_comparisons
return (a, e, b, d, c), n_comparisons
if lt(b, c):
return (a, e, d, b, c), n_comparisons
return (a, e, d, c, b), n_comparisons
if lt(b, c):
if lt(b, d):
return (e, a, b, d, c), n_comparisons
return (e, a, d, b, c), n_comparisons
return (e, a, d, c, b), n_comparisons
if lt(a, e):
if lt(b, e):
if lt(b, c):
if lt(c, e):
return (d, a, b, c, e), n_comparisons
return (d, a, b, e, c), n_comparisons
if lt(a, c):
return (d, a, c, b, e), n_comparisons
return (d, c, a, b, e), n_comparisons
if lt(c, e):
if lt(a, c):
return (d, a, c, e, b), n_comparisons
return (d, c, a, e, b), n_comparisons
if lt(b, c):
return (d, a, e, b, c), n_comparisons
return (d, a, e, c, b), n_comparisons
if lt(a, c):
if lt(b, c):
if lt(d, e):
return (d, e, a, b, c), n_comparisons
return (e, d, a, b, c), n_comparisons
if lt(d, e):
return (d, e, a, c, b), n_comparisons
return (e, d, a, c, b), n_comparisons
if lt(c, e):
return (d, c, e, a, b), n_comparisons
if lt(d, e):
return (d, e, c, a, b), n_comparisons
return (e, d, c, a, b), n_comparisons
if lt(c, d):
if lt(a, d):
if lt(a, e):
if lt(a, c):
if lt(c, e):
if lt(d, e):
return (b, a, c, d, e), n_comparisons
return (b, a, c, e, d), n_comparisons
return (b, a, e, c, d), n_comparisons
if lt(b, c):
if lt(d, e):
return (b, c, a, d, e), n_comparisons
return (b, c, a, e, d), n_comparisons
if lt(d, e):
return (c, b, a, d, e), n_comparisons
return (c, b, a, e, d), n_comparisons
if lt(b, e):
if lt(c, e):
if lt(b, c):
return (b, c, e, a, d), n_comparisons
return (c, b, e, a, d), n_comparisons
if lt(a, c):
return (b, e, a, c, d), n_comparisons
return (b, e, c, a, d), n_comparisons
if lt(b, c):
if lt(a, c):
return (e, b, a, c, d), n_comparisons
return (e, b, c, a, d), n_comparisons
if lt(c, e):
return (c, e, b, a, d), n_comparisons
return (e, c, b, a, d), n_comparisons
if lt(d, e):
if lt(a, e):
if lt(b, c):
return (b, c, d, a, e), n_comparisons
if lt(b, d):
return (c, b, d, a, e), n_comparisons
return (c, d, b, a, e), n_comparisons
if lt(b, d):
if lt(b, c):
return (b, c, d, e, a), n_comparisons
return (c, b, d, e, a), n_comparisons
if lt(b, e):
return (c, d, b, e, a), n_comparisons
return (c, d, e, b, a), n_comparisons
if lt(c, e):
if lt(b, e):
if lt(b, c):
return (b, c, e, d, a), n_comparisons
return (c, b, e, d, a), n_comparisons
if lt(b, d):
return (c, e, b, d, a), n_comparisons
return (c, e, d, b, a), n_comparisons
if lt(b, c):
if lt(b, e):
return (b, e, c, d, a), n_comparisons
return (e, b, c, d, a), n_comparisons
if lt(b, d):
return (e, c, b, d, a), n_comparisons
return (e, c, d, b, a), n_comparisons
if lt(a, c):
if lt(a, e):
if lt(a, d):
if lt(c, e):
return (b, a, d, c, e), n_comparisons
if lt(d, e):
return (b, a, d, e, c), n_comparisons
return (b, a, e, d, c), n_comparisons
if lt(b, d):
if lt(c, e):
return (b, d, a, c, e), n_comparisons
return (b, d, a, e, c), n_comparisons
if lt(c, e):
return (d, b, a, c, e), n_comparisons
return (d, b, a, e, c), n_comparisons
if lt(b, e):
if lt(d, e):
if lt(b, d):
return (b, d, e, a, c), n_comparisons
return (d, b, e, a, c), n_comparisons
if lt(a, d):
return (b, e, a, d, c), n_comparisons
return (b, e, d, a, c), n_comparisons
if lt(b, d):
if lt(a, d):
return (e, b, a, d, c), n_comparisons
return (e, b, d, a, c), n_comparisons
if lt(d, e):
return (d, e, b, a, c), n_comparisons
return (e, d, b, a, c), n_comparisons
if lt(c, e):
if lt(a, e):
if lt(b, c):
if lt(b, d):
return (b, d, c, a, e), n_comparisons
return (d, b, c, a, e), n_comparisons
return (d, c, b, a, e), n_comparisons
if lt(b, c):
if lt(b, d):
return (b, d, c, e, a), n_comparisons
return (d, b, c, e, a), n_comparisons
if lt(b, e):
return (d, c, b, e, a), n_comparisons
return (d, c, e, b, a), n_comparisons
if lt(d, e):
if lt(b, e):
if lt(b, d):
return (b, d, e, c, a), n_comparisons
return (d, b, e, c, a), n_comparisons
if lt(b, c):
return (d, e, b, c, a), n_comparisons
return (d, e, c, b, a), n_comparisons
if lt(b, d):
if lt(b, e):
return (b, e, d, c, a), n_comparisons
return (e, b, d, c, a), n_comparisons
if lt(b, c):
return (e, d, b, c, a), n_comparisons
return (e, d, c, b, a), n_comparisons
Derivation
from typing import Set, List, Tuple
from string import ascii_letters
from itertools import permutations, combinations
def build_decision_tree(initial_permutations: Set[int],
conditional_permutations: List[Set[Tuple[int]]]):
if len(initial_permutations) == 1:
return initial_permutations.pop()
# Find condition that splits `initial_permutations` in the most balanced way.
target = len(initial_permutations) / 2
condition_index = 0
condition_sizes = [len(initial_permutations & perms)
for perms in conditional_permutations]
condition_index = min(range(len(conditional_permutations)),
key = lambda i: abs(condition_sizes[i] - target))
permutations_true = initial_permutations & conditional_permutations[condition_index]
permutations_false = initial_permutations - permutations_true
return (condition_index,
(build_decision_tree(permutations_true, conditional_permutations),
build_decision_tree(permutations_false, conditional_permutations)))
def get_sort_function_string(decision_tree, conditions, indent=4):
indentation = " " * indent
if isinstance(decision_tree[1], int):
return_statement = f"return {', '.join([ascii_letters[x] for x in decision_tree])}\n"
return indentation + return_statement
else:
i, j = conditions[decision_tree[0]]
condition_string = f"{indentation}if {ascii_letters[i]} < {ascii_letters[j]}:\n"
true_subtree, false_subtree = decision_tree[1]
true_subtree_string = get_sort_function_string(true_subtree, conditions, indent + 4)
false_subtree_string = get_sort_function_string(false_subtree, conditions, indent)
return condition_string + true_subtree_string + false_subtree_string
def generate_sorting_logic(n_items: int):
permutations_n = set(permutations(range(n_items)))
conditions = list(combinations(range(n_items), 2))
conditional_permutations = [{p for p in permutations_n if p.index(i) < p.index(j)}
for i, j in conditions]
tree = build_decision_tree(permutations_n, conditional_permutations)
function_arguments = ", ".join([ascii_letters[i] for i in range(n_items)])
function_header = f"def sort_{n_items}_items({function_arguments}):\n"
return function_header + get_sort_function_string(tree, conditions)
def check_sorter(n_items, sorter):
sorted_range = tuple(range(n_items))
for p in permutations(range(n_items)):
sorted_p_actual = sorter(*p)
assert sorted_p_actual == sorted_range, f"Expected {sorted_range}, got {sorted_p_actual}"
print(f"All permutations of {n_items} items were sorted correctly.")
n_items = 5
sorter_string = generate_sorting_logic(n_items)
#print(sorter_string)
exec(sorter_string)
check_sorter(n_items, eval(f"sort_{n_items}_items"))
We can see that the above derivation (which chooses comparisons that block out half the possibilities after each comparison) produces sorting functions that have a time complexity of O(log(n!)), which is equivalent to O(nlogn).
Further reading: Number of comparisons required to sort a list (table)
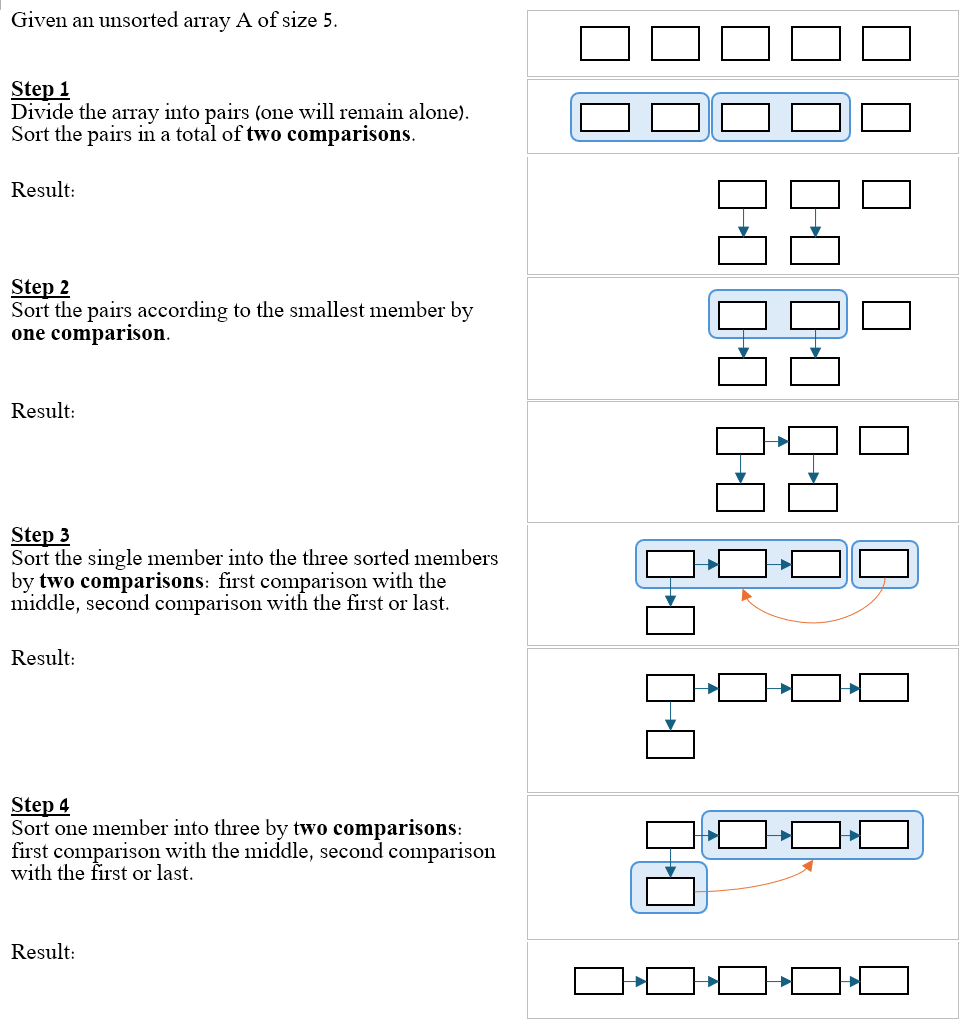
Here is an elaborate algorithm with Pseudocode and Python code.
Algorithm:
Pseudocode:
SORT_5_IN_7(A)
// 1. Sort {A[1], A[2]} and {A[3], A[4]} with a total of 2 compares.
if A [1] > A[2]
reorder A[1], A[2] ⇒ A[2], A[1]
if A[3] > A[4]
reorder A[3], A[4] ⇒ A[4], A[3]
// 2. Sort {A[1], A[2]} and {A[3], A[4]} by the first item with 1 compare.
if A[1] > A[3]
reorder A[1], A[2], A[3], A[4] ⇒ A[3], A[4], A[1], A[2]
// 3. Sort A[5] into {A[1], A[3], A[4]} with 2 compares.
if A[5] > A[3]
if A[5] < A[4]
reorder A[4], A[5] ⇒ A[5], A[4]
else
if A[5] > A[1]
reorder A[3], A[4], A[5] ⇒ A[5], A[3], A[4]
else
reorder A[1], A[3], A[4], A[5] ⇒ A[5], A[1], A[3], A[4]
// 4. Sort A[2] into {A[3], A[4], A[5]} with 2 compares.
if A[2] > A[4]
if A[2] > A[5]
reorder A[2], A[3], A[4], A[5] ⇒ A[3], A[4], A[5], A[2]
else
reorder A[2], A[3], A[4] ⇒ A[3], A[4], A[2]
else
if A[2] > A[3]
reorder A[2], A[3] ⇒ A[3], A[2]
Python code:
from itertools import permutations
def sort5in7(A):
A = list(A)
# 1. Sort {A[0], A[1]} and {A[2], A[3]} with a total of 2 compares.
if A[0] > A[1]:
A[0], A[1] = A[1], A[0]
if A[2] > A[3]:
A[2], A[3] = A[3], A[2]
# 2. Sort {A[0], A[1]} and {A[2], A[3]} by the first item with 1 compare.
if A[0] > A[2]:
A[0], A[1], A[2], A[3] = A[2], A[3], A[0], A[1]
# 3. Sort A[4] into {A[0], A[2], A[3]} with 2 compares.
if A[4] > A[2]:
if A[4] < A[3]:
A[3], A[4] = A[4], A[3]
else:
if A[4] > A[0]:
A[2], A[3], A[4] = A[4], A[2], A[3]
else:
A[0], A[2], A[3], A[4] = A[4], A[0], A[2], A[3]
# 4. Sort A[1] into {A[2], A[3], A[4]} with 2 compares.
if A[1] > A[3]:
if A[1] > A[4]:
A[1], A[2], A[3], A[4] = A[2], A[3], A[4], A[1]
else:
A[1], A[2], A[3] = A[2], A[3], A[1]
else:
if A[1] > A[2]:
A[1], A[2] = A[2], A[1]
return A
assert all(list(sort5in7(p)) == sorted(p) for p in permutations(range(5)))
perms = list(permutations(range(5)))
print("Permutation count:", len(perms))
for p in perms:
p1 = sorted(p)
p2 = sort5in7(p)
print(p, p1, p2, p1 == p2)
© 2022 - 2024 — McMap. All rights reserved.