fast algorithm for drawing filled circles?

Question

I am using Bresenham's circle algorithm for fast circle drawing. However, I also want to (at the request of the user) draw a filled circle.

Is there a fast and efficient way of doing this? Something along the same lines of Bresenham?

The language I am using is C.

Denby

Answer 1

Having read the Wikipedia page on Bresenham's (also 'Midpoint') circle algorithm, it would appear that the easiest thing to do would be to modify its actions, such that instead of

setPixel(x0 + x, y0 + y);
setPixel(x0 - x, y0 + y);

and similar, each time you instead do

lineFrom(x0 - x, y0 + y, x0 + x, y0 + y);

That is, for each pair of points (with the same y) that Bresenham would you have you plot, you instead connect with a line.

Prisage

does that really work ? i tried it .. it doesn't totally fill the circle. Am I missing something ? In any case, there are some correct answers below. – Haemoglobin

@Haemoglobin To know if you're missing something, we'd need to see your code, in a new question of your own – Prisage

Wouldn't this cause scan lines in the 2nd/3rd and 6th/7th quadrants to be repeated? In those x changes at every step and the decision variable governs y. – Rhabdomancy

@Prisage ok it seems I have misread the answer , it seems like a scan line algorithm which would do. I dont remember exactly but i think had connected the symmetric point 180 deg apart to make the lines and that doesnt work as lot of them overlap. Make some edit to answer so that I can remove by downvote. – Epigoni

I am trying to have for border a color, and for fill another color. I to exactly what you said and after i construct the border with the basic command for the algorithm. the problem is that in the upper and bottom parts of the circle, the border is covered by the fill color, Any idea why ? – Yonne

@Loki that sounds like a new question really, but sounds like you want the setPixel commands in normal Bresenham and a lineFrom command that omits the end pixels. – Prisage

@Prisage i solved it. When i am drawing the lines i use drawLines(circle.center, p, q-1); – Yonne

hi, any clue how to have the same kind of algorithm without line overlapping? – Aldas

@Aldas not sure what you mean, sounds like you need to ask a new question – Prisage

well I'm using this algorithm but I see that this algorithm draw twice even three times the same pixel, also when it does'nt I have at the top of the circle 3 lines overlapping of different width (I'm drawing squares I'm not using pixel's screen) I'll probably ask a new question. But if you have a clue I'll take it . Thanks – Aldas

Answer 2

Just use brute force. This method iterates over a few too many pixels, but it only uses integer multiplications and additions. You completely avoid the complexity of Bresenham and the possible bottleneck of sqrt.

for(int y=-radius; y<=radius; y++)
    for(int x=-radius; x<=radius; x++)
        if(x*x+y*y <= radius*radius)
            setpixel(origin.x+x, origin.y+y);

Noachian

I like this answer because it solves the problem in a very direct way. The only problem with this is that it generates a different circle than the midpoint circle algorithm. These circles are "thinner" than the equivalent in midpoint, which appear to be the more correct shape. Any way to fix that? – Falsecard

This sounds horrible, but I found that in most cases I can get the exact same circle from this algorithm as midpoint if I modify the check slightly. Those times it doesn't exactly match up, it's pretty close. The modification to the check is: x * x + y * y <= range * range + range * 0.8f – Falsecard

I had the same issue as Dwight, but to avoid the float cast just replaced the if statement with this one: if(x*x+y*y < radius*radius + radius) also to get just the circle (ring) you can do this if(x*x+y*y > radius*radius - radius && x*x+y*y < radius*radius + radius) – Gardy

@Gardy To avoid the float cast you added a whole new branch and 5 new arithmetic operations and that's supposed to be faster? – Ephesus

@Ephesus There are no extra operations, replaced <= with < and radius * 0.8f with + radius the other if statement is unrelated (for when you want just an outline). – Gardy

Answer 3

Here's a C# rough guide (shouldn't be that hard to get the right idea for C) - this is the "raw" form without using Bresenham to eliminate repeated square-roots.

Bitmap bmp = new Bitmap(200, 200);

int r = 50; // radius
int ox = 100, oy = 100; // origin

for (int x = -r; x < r ; x++)
{
    int height = (int)Math.Sqrt(r * r - x * x);

    for (int y = -height; y < height; y++)
        bmp.SetPixel(x + ox, y + oy, Color.Red);
}

bmp.Save(@"c:\users\dearwicker\Desktop\circle.bmp");

Radley

Or loop on y and draw horizonal lines. Occasionally there is a reason to choose one or the other, but in most cases it does not matter. Either way you use the same Bresenham logic to find the endpoints quickly. – Laina

No, but you can use Bresenham to avoid that. The basic idea is to "join the dots" between the upper and lower points at each x coordinate covered by the circle. – Radley

Profile to see which is best. If there's a difference at all, going horizontal should be better. It gets rid of a multiplication by stride and may result in fewer faults. – Astri

@Prisage - have you tried it? I find it makes almost no measurable difference whether I compute the Math.Sqrt or not. (Obviously I've eliminated the SetPixel as well, which accounts for ALL the time in the complete program; I just add x and y to a counter variable to ensure they're used). – Radley

"All those Math.Sqrts aren't going to be especially fast" - the disassembly shows that the C#/JIT combo emits the inlined SQRTSD instruction on my 64-bit machine, and so it's little wonder that it runs blazingly fast. I can't measure a different between Math.Sqrt and a simple addition. So I think your comment is probably based on pre-FP instruction set guessing! – Radley

This is surprising to me too, as it's been a while since I've had to use Sqrt for anything, so I've blogged it here: smellegantcode.wordpress.com/2009/07/29/square-roots-are-slow – Radley

That perennial problem - what to do with one's carefully-tuned educated-guesswork engine when the fundamentals change? – Prisage

Well, depends if you want to learn about history or get the job done - personally I enjoy both! :) – Radley

Yup, looping on y makes more sense when blitting on a framebuffer. – Gelasius

Congrats, according to my tests on quick-bench, your solution is by far the fastest! quick-bench.com/mwTOodNOI81k1ddaTCGH_Cmn_Ag – Endoenzyme

Answer 4

You can use this:

void DrawFilledCircle(int x0, int y0, int radius)
{
    int x = radius;
    int y = 0;
    int xChange = 1 - (radius << 1);
    int yChange = 0;
    int radiusError = 0;

    while (x >= y)
    {
        for (int i = x0 - x; i <= x0 + x; i++)
        {
            SetPixel(i, y0 + y);
            SetPixel(i, y0 - y);
        }
        for (int i = x0 - y; i <= x0 + y; i++)
        {
            SetPixel(i, y0 + x);
            SetPixel(i, y0 - x);
        }

        y++;
        radiusError += yChange;
        yChange += 2;
        if (((radiusError << 1) + xChange) > 0)
        {
            x--;
            radiusError += xChange;
            xChange += 2;
        }
    }
}

Artistic

Answer 5

Great ideas here! Since I'm at a project that requires many thousands of circles to be drawn, I have evaluated all suggestions here (and improved a few by precomputing the square of the radius):

http://quick-bench.com/mwTOodNOI81k1ddaTCGH_Cmn_Ag

The Rev variants just have x and y swapped because consecutive access along the y axis are faster with the way my grid/canvas structure works.

The clear winner is Daniel Earwicker's method ( DrawCircleBruteforcePrecalc ) that precomputes the Y value to avoid unnecessary radius checks. Somewhat surprisingly that negates the additional computation caused by the sqrt call.

Some comments suggest that kmillen's variant (DrawCircleSingleLoop) that works with a single loop should be very fast, but it's the slowest here. I assume that is because of all the divisions. But perhaps I have adapted it wrong to the global variables in that code. Would be great if someone takes a look.

EDIT: After looking for the first time since college years at some assembler code, I managed find that the final additions of the circle's origin are a culprit. Precomputing those, I improved the fastest method by a factor of another 3.7-3.9 according to the bench! http://quick-bench.com/7ZYitwJIUgF_OkDUgnyMJY4lGlA Amazing.

This being my code:

for (int x = -radius; x < radius ; x++)
{
    int hh = (int)std::sqrt(radius_sqr - x * x);
    int rx = center_x + x;
    int ph = center_y + hh;

    for (int y = center_y-hh; y < ph; y++)
        canvas[rx][y] = 1;
}

Endoenzyme

Answer 6

I like palm3D's answer. For being brute force, this is an amazingly fast solution. There are no square root or trigonometric functions to slow it down. Its one weakness is the nested loop.

Converting this to a single loop makes this function almost twice as fast.

int r2 = r * r;
int area = r2 << 2;
int rr = r << 1;

for (int i = 0; i < area; i++)
{
    int tx = (i % rr) - r;
    int ty = (i / rr) - r;

    if (tx * tx + ty * ty <= r2)
        SetPixel(x + tx, y + ty, c);
}

This single loop solution rivals the efficiency of a line drawing solution.

            int r2 = r * r;
            for (int cy = -r; cy <= r; cy++)
            {
                int cx = (int)(Math.Sqrt(r2 - cy * cy) + 0.5);
                int cyy = cy + y;

                lineDDA(x - cx, cyy, x + cx, cyy, c);
            }

Bimonthly

I'm a bit surprised that your solution is faster than palm3d. Did you measure it ? do you have numbers ? – Odelet

This algorithm draws less pixels than the original. For a radius of 10, it does 41 loops less.. On my laptop, running 100,000,000 tests of this function and the original, we get: ORIGINAL: 43ns. THIS: 42ns on a good run.. On a bad run: ORIGINAL: 87ns. THIS: 54ns.. but these are nano-seconds so in terms of efficiency, there's virtually no difference. Tested on: Intel(R) Core(TM) i7-4980HQ CPU @ 2.80GHz – Scots

Hmm, am quite confused to where this is supposed to be faster.. Am currently trying all variants in quick-bench.com/VtgMOwU8IQoa7biFNHFZ2ws5hlk and it is much, much slower. That doe snot really surprise me though because divisions are often very slow. – Endoenzyme

Answer 7

palm3D's brute-force algorithm I found to be a good starting point. This method uses the same premise, however it includes a couple of ways to skip checking most of the pixels.

First, here's the code:

int largestX = circle.radius;
for (int y = 0; y <= radius; ++y) {
    for (int x = largestX; x >= 0; --x) {
        if ((x * x) + (y * y) <= (circle.radius * circle.radius)) {
            drawLine(circle.center.x - x, circle.center.x + x, circle.center.y + y);
            drawLine(circle.center.x - x, circle.center.x + x, circle.center.y - y);
            largestX = x;
            break; // go to next y coordinate
        }
    }
}

Next, the explanation.

The first thing to note is that if you find the minimum x coordinate that is within the circle for a given horizontal line, you immediately know the maximum x coordinate. This is due to the symmetry of the circle. If the minimum x coordinate is 10 pixels ahead of the left of the bounding box of the circle, then the maximum x is 10 pixels behind the right of the bounding box of the circle.

The reason to iterate from high x values to low x values, is that the minimum x value will be found with less iterations. This is because the minimum x value is closer to the left of the bounding box than the centre x coordinate of the circle for most lines, due to the circle being curved outwards, as seen on this image The next thing to note is that since the circle is also symmetric vertically, each line you find gives you a free second line to draw, each time you find a line in the top half of the circle, you get one on the bottom half at the radius-y y coordinate. Therefore, when any line is found, two can be drawn and only the top half of the y values needs to be iterated over.

The last thing to note is that is that if you start from a y value that is at the centre of the circle and then move towards the top for y, then the minimum x value for each next line must be closer to the centre x coordinate of the circle than the last line. This is also due to the circle curving closer towards the centre x value as you go up the circle. Here is a visual on how that is the case.

In summary:

1. If you find the minimum x coordinate of a line, you get the maximum x coordinate for free.
2. Every line you find to draw on the top half of the circle gives you a line on the bottom half of the circle for free.
3. Every minimum x coordinate has to be closer to the centre of the circle than the previous x coordinate for each line when iterating from the centre y coordinate to the top.

You can also store the value of (radius * radius), and also (y * y) instead of calculating them multiple times.

Jobyna

Answer 8

Here's how I'm doing it:
I'm using fixed point values with two bits precision (we have to manage half points and square values of half points)
As mentionned in a previous answer, I'm also using square values instead of square roots.
First, I'm detecting border limit of my circle in a 1/8th portion of the circle. I'm using symetric of these points to draw the 4 "borders" of the circle. Then I'm drawing the square inside the circle.

Unlike the midpoint circle algorith, this one will work with even diameters (and with real numbers diameters too, with some little changes).

Please forgive me if my explanations were not clear, I'm french ;)

void DrawFilledCircle(int circleDiameter, int circlePosX, int circlePosY)
{
    const int FULL = (1 << 2);
    const int HALF = (FULL >> 1);

    int size = (circleDiameter << 2);// fixed point value for size
    int ray = (size >> 1);
    int dY2;
    int ray2 = ray * ray;
    int posmin,posmax;
    int Y,X;
    int x = ((circleDiameter&1)==1) ? ray : ray - HALF;
    int y = HALF;
    circlePosX -= (circleDiameter>>1);
    circlePosY -= (circleDiameter>>1);

    for (;; y+=FULL)
    {
        dY2 = (ray - y) * (ray - y);

        for (;; x-=FULL)
        {
            if (dY2 + (ray - x) * (ray - x) <= ray2) continue;

            if (x < y)
            {
                Y = (y >> 2);
                posmin = Y;
                posmax = circleDiameter - Y;

                // Draw inside square and leave
                while (Y < posmax)
                {
                    for (X = posmin; X < posmax; X++)
                        setPixel(circlePosX+X, circlePosY+Y);
                    Y++;
                }
                // Just for a better understanding, the while loop does the same thing as:
                // DrawSquare(circlePosX+Y, circlePosY+Y, circleDiameter - 2*Y);
                return;
            }

            // Draw the 4 borders
            X = (x >> 2) + 1;
            Y = y >> 2;
            posmax = circleDiameter - X;
            int mirrorY = circleDiameter - Y - 1;

            while (X < posmax)
            {
                setPixel(circlePosX+X, circlePosY+Y);
                setPixel(circlePosX+X, circlePosY+mirrorY);
                setPixel(circlePosX+Y, circlePosY+X);
                setPixel(circlePosX+mirrorY, circlePosY+X);
                X++;
            }
            // Just for a better understanding, the while loop does the same thing as:
            // int lineSize = circleDiameter - X*2;
            // Upper border:
            // DrawHorizontalLine(circlePosX+X, circlePosY+Y, lineSize);
            // Lower border:
            // DrawHorizontalLine(circlePosX+X, circlePosY+mirrorY, lineSize);
            // Left border:
            // DrawVerticalLine(circlePosX+Y, circlePosY+X, lineSize);
            // Right border:
            // DrawVerticalLine(circlePosX+mirrorY, circlePosY+X, lineSize);

            break;
        }
    }
}

void DrawSquare(int x, int y, int size)
{
    for( int i=0 ; i<size ; i++ )
        DrawHorizontalLine(x, y+i, size);
}

void DrawHorizontalLine(int x, int y, int width)
{
    for(int i=0 ; i<width ; i++ )
        SetPixel(x+i, y);
}

void DrawVerticalLine(int x, int y, int height)
{
    for(int i=0 ; i<height ; i++ )
        SetPixel(x, y+i);
}

To use non-integer diameter, you can increase precision of fixed point or use double values. It should even be possible to make a sort of anti-alias depending on the difference between dY2 + (ray - x) * (ray - x) and ray2 (dx² + dy² and r²)

Leschen

Answer 9

If you want a fast algorithm, consider drawing a polygon with N sides, the higher is N, the more precise will be the circle.

Hild

this would probably require some kind of hardware acceleration to be fastest – Kitchener

Answer 10

I would just generate a list of points and then use a polygon draw function for the rendering.

Wine

If he has implemented Bresenham for the open version, he is working at a lower layer then using an API...either for learning purposes or to implement an API. – Laina

Answer 11

It may not be the algorithm yo are looking for and not the most performant one,
but I always do something like this:

void fillCircle(int x, int y, int radius){

   // fill a circle
   for(int rad = radius; rad >= 0; rad--){

      // stroke a circle
      for(double i = 0; i <= PI * 2; i+=0.01){

         int pX = x + rad * cos(i);
         int pY = y + rad * sin(i);

         drawPoint(pX, pY);

      }

   }

}

Lipread

Answer 12

The following two methods avoid the repeated square root calculation by drawing multiple parts of the circle at once and should therefore be quite fast:

void circleFill(const size_t centerX, const size_t centerY, const size_t radius, color fill) {
    if (centerX < radius || centerY < radius || centerX + radius > width || centerY + radius > height) 
        return;

    const size_t signedRadius = radius * radius;
    for (size_t y = 0; y < radius; y++) {
        const size_t up = (centerY - y) * width;
        const size_t down = (centerY + y) * width;
        const size_t halfWidth = roundf(sqrtf(signedRadius - y * y));
        for (size_t x = 0; x < halfWidth; x++) {
            const size_t left = centerX - x;
            const size_t right = centerX + x;
            pixels[left + up] = fill;
            pixels[right + up] = fill;
            pixels[left + down] = fill;
            pixels[right + down] = fill;
        }
    }
}


void circleContour(const size_t centerX, const size_t centerY, const size_t radius, color stroke) {
    if (centerX < radius || centerY < radius || centerX + radius > width || centerY + radius > height) 
        return;
    
    const size_t signedRadius = radius * radius;
    const size_t maxSlopePoint = ceilf(radius * 0.707106781f); //ceilf(radius * cosf(TWO_PI/8));

    for (size_t i = 0; i < maxSlopePoint; i++) {
        const size_t depth = roundf(sqrtf(signedRadius - i * i));

        size_t left = centerX - depth;
        size_t right = centerX + depth;
        size_t up = (centerY - i) * width;
        size_t down = (centerY + i) * width;

        pixels[left + up] = stroke;
        pixels[right + up] = stroke;
        pixels[left + down] = stroke;
        pixels[right + down] = stroke;

        left = centerX - i;
        right = centerX + i;
        up = (centerY - depth) * width;
        down = (centerY + depth) * width;

        pixels[left + up] = stroke;
        pixels[right + up] = stroke;
        pixels[left + down] = stroke;
        pixels[right + down] = stroke;
    }
}

Camey

Answer 13

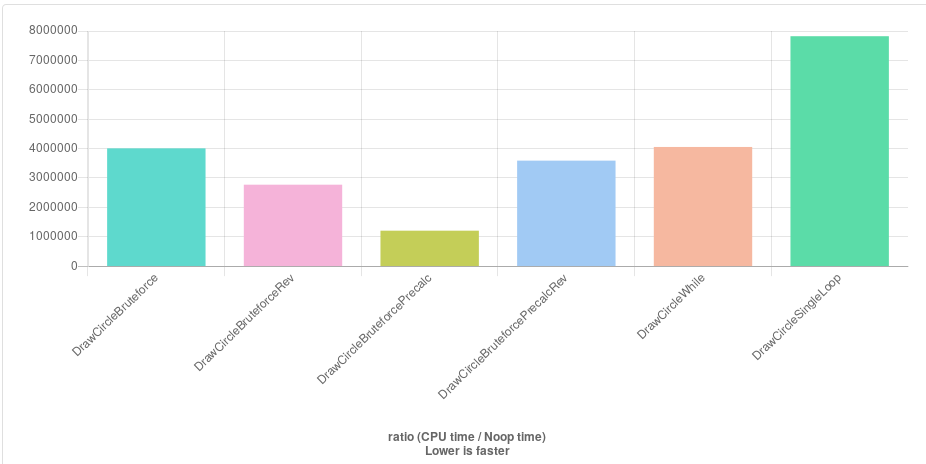
This was used in my new 3D printer Firmware, and it is proven the fastest way for filled circle of a diameter from 1 to 43 pixel. If larger is needed, the following memory block(or array) should be extended following a structure I wont waste my time explaining...

If you have questions, or need larger diameter than 43, contact me, I will help you drawing the fastest and perfect filled circles... or Bresenham's circle drawing algorithm can be used above those diameters, but having to fill the circle after, or incorporating the fill into Bresenham's circle drawing algorithm, will only result in slower fill circle than my code. I already benchmarked the different codes, my solution is 4 to 5 times faster. As a test I have been able to draw hundreds of filled circles of different size and colors on a BigTreeTech tft24 1.1 running on a 1-core 72 Mhz cortex-m4

https://www.youtube.com/watch?v=7_Wp5yn3ADI

// this must be declared anywhere, as static or global
// as long as the function can access it !

 uint8_t Rset[252]={
  0,1,1,2,2,1,2,3,3,1,3,3,4,4,2,3,4,5,5,5,2,4,5,5,
  6,6,6,2,4,5,6,6,7,7,7,2,4,5,6,7,7,8,8,8,2,5,6,7,
  8,8,8,9,9,9,3,5,6,7,8,9,9,10,10,10,10,3,5,7,8,9,
  9,10,10,11,11,11,11,3,5,7,8,9,10,10,11,11,12,12,
  12,12,3,6,7,9,10,10,11,12,12,12,13,13,13,13,3,6,
  8,9,10,11,12,12,13,13,13,14,14,14,14,3,6,8,9,10,
  11,12,13,13,14,14,14,15,15,15,15,3,6,8,10,11,12,
  13,13,14,14,15,15,15,16,16,16,16,4,7,8,10,11,12,
  13,14,14,15,16,16,16,17,17,17,17,17,4,7,9,10,12,
  13,14,14,15,16,16,17,17,17,18,18,18,18,18,4,7,9,
  11,12,13,14,15,16,16,17,17,18,18,18,19,19,19,19,
  19,7,9,11,12,13,15,15,16,17,18,18,19,19,20,20,20,
  20,20,20,20,20,7,9,11,12,14,15,16,17,17,18,19,19
  20,20,21,21,21,21,21,21,21,21};   
  
       // SOLUTION 1: (the fastest)
       
void FillCircle_v1(uint16_t x, uint16_t y, uint16_t r)
 { 
   // all needed variables are created and set to their value...
   uint16_t radius=(r<1) ? 1 : r ;
   if (radius>21 ) {radius=21; }
   uint16_t diam=(radius*2)+1;
   uint16_t ymir=0, cur_y=0;
   radius--; uint16_t target=(radius*radius+3*radius)/2; radius++;
 // this part draws directly into the ILI94xx TFT buffer mem. 
 // using pointers..2 versions where you can draw 
 // pixels and lines with coordinates will follow
   for (uint16_t yy=0; yy<diam; yy++) 
   { ymir= (yy<=radius) ? yy+target : target+diam-(yy+1);
   cur_y=y-radius+yy;
   uint16_t *pixel=buffer_start_addr+x-Rset[ymir]+cur_y*buffer_width;
   for (uint16_t xx= 0; xx<=(2*Rset[ymir]); xx++) 
   { *pixel++ = CANVAS::draw_color; }}} 



  // SOLUTION 2: adaptable to any system that can 
  // add a pixel at a time: (drawpixel or add_pixel,etc_)
  
void FillCircle_v2(uint16_t x, uint16_t y, uint16_t r)
 { 
   // all needed variables are created and set to their value...
   uint16_t radius=(r<1) ? 1 : r ;
   if (radius>21 ) {radius=21; }
   uint16_t diam=(radius*2)+1;
   uint16_t ymir=0, cur_y=0;
   radius--; uint16_t target=(radius*radius+3*radius)/2; radius++;
  for (uint16_t yy=0; yy<diam; yy++) 
  { ymir= (yy<=radius) ? yy+target : target+diam-(yy+1);
    cur_y=y-radius+yy;
    uint16_t Pixel_x=x-Rset[ymir];
    for (uint16_t xx= 0; xx<=(2*Rset[ymir]); xx++) 
     { //use your add_pixel or draw_pixel here
       // using those coordinates:
       // X position will be... (Pixel_x+xx)
       // Y position will be... (cur_y)
       // and add those 3 brackets at the end
   }}} 



  // SOLUTION 3: adaptable to any system that can draw fast 
  //                horizontal lines
 void FillCircle_v3(uint16_t x, uint16_t y, uint16_t r)
  { 
   // all needed variables are created and set to their value...
   uint16_t radius=(r<1) ? 1 : r ;
   if (radius>21 ) {radius=21; }
   uint16_t diam=(radius*2)+1;
   uint16_t ymir=0, cur_y=0;
   radius--; uint16_t target=(radius*radius+3*radius)/2; radius++;
   for (uint16_t yy=0; yy<diam; yy++) 
   { ymir= (yy<=radius) ? yy+target : target+diam-(yy+1);  
   cur_y=y-radius+yy;
   uint16_t start_x=x-Rset[ymir];
   uint16_t width_x=2*Rset[ymir];

   //  ... then use your best drawline function using those values:
   //  start_x:   position X of the start of the line
   //  cur_y:     position Y of the current line
   //  width_x:   length of the line
   //  if you need a 2nd coordinate then :end_x=start_x+width_x
   // and add those 2 brackets after !!!
 
    }}

Stomach

Answer 14

I did pretty much what AlegGeorge did but I changed three lines. I thought that this is faster but these are the results am I doing anything wrong? my function is called DrawBruteforcePrecalcV4. here's the code:

for (int x = 0; x < radius ; x++) // Instead of looping from -radius to radius I loop from 0 to radius
{
    int hh = (int)std::sqrt(radius_sqr - x * x);
    int rx = center_x + x;
    int cmx = center_x - x;
    int ph = center_y+hh;

    for (int y = center_y-hh; y < ph; y++)
    {
      canvas[rx][y] = 1;
      canvas[cmx][y] = 1;
    }
}

Disparate