How can I find the minimum cut on a graph using a maximum flow algorithm?

Question

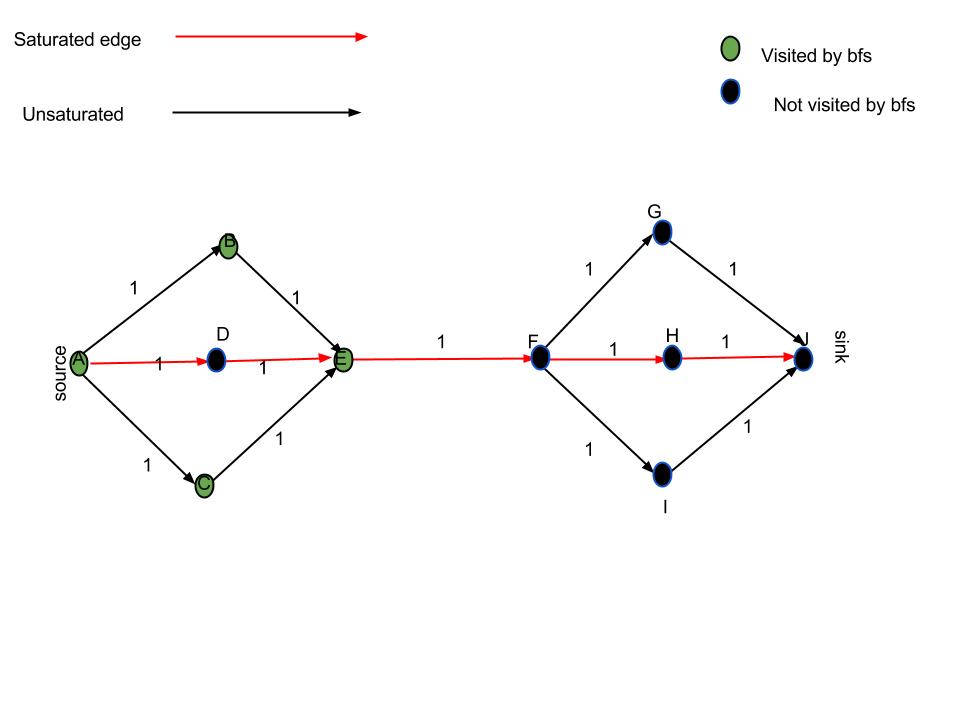
I need to find the minimum cut on a graph. I've been reading about flow networks, but all I can find are maximum flow algorithms such as Ford-Fulkerson, push-relabel, etc. Given the max flow-min cut theorem, is it possible to use one of those algorithms to find the minimum cut on a graph using a maximum flow algorithm? How?

The best information I have found so far is that if I find "saturated" edges i.e. edges where flow equals capacity, those edges correspond to the minimum cut. Is that true? It doesn't sound 100% right to me. It is true that all edges on the minimum cut will be saturated, but I believe there might also be saturated edges which are out of the minimum cut "path".

Debauchery

Answer 1

From the source vertex, do a depth-first search along edges in the residual network (i.e., non-saturated edges and back edges of edges that have flow), and mark all vertices that can be reached this way. The cut consists of all edges that go from a marked to an unmarked vertex. Clearly, those edges are saturated and thus were not traversed. As you noted, there might be other saturated edges that are not part of the minimum cut.

Thimbleweed

I'm not sure that I understand your description. In this graph: i.imgur.com/5TRQ0h2.png I feel like your algorithm says that the min cut would be to remove the 40/40 edge and the 50/50 edge. – Homogeneous

@NiklasB. I have edited my description to be hopefully more clear. – Infract

This is not always correct, for DAGs it will be fine. See answer of dingalapadum – Jannet

Should I do DFS on every node, or just on source? – Tick

Just from the source. – Infract

I think we want only edges from an s-reachable vertex in the residual graph to an s-unreachable vertex. E.g. consider the graph with edges {sx, sy, sz, xy, zy, xt, yt}, all of capacity 1. There's a max flow (of 2) in which {sx, xt, sy, yt} all have flow 1, and s, y and z are s-reachable in this flow's residual graph, so if we take all edges with one visited and one unvisited endpoint as you suggest, we get {sx, yt, xy} as the min-cutset -- but xy (which has 0 flow) shouldn't be there. – Supersonic

Answer 2

I don't want to be picky, but the suggested solution is not quite right as proposed.

Correct solution: What you actually should be doing is bfs/dfs on the Residual-Network Gf (read it up on wikipedia) and marking vertices. And then you can pick those with marked from-vertex and unmarked to-vertex.

Why 'following unsaturated edges' is not enough: Consider, that the flow algorithm saturates the edges as shown in the picture. I marked the vertices I'm visiting with the approach of "just following unsaturated edges" with green. Clearly the only correct min-cut is the edge from E-F, while the suggested solution would also return A-D (and maybe even D-E).

Note that the vertex D would be visited by the dfs/bfs if we considered the Residual network instead, because there'd be an edge from E to D, thereby making the edge E-F the only one with a marked from-vertex and an unmarked to-vertex.

Leund

You're not picky! The above answers are wrong. Thanks. – Jannet

This is exactly what I was looking for! A note that D IS visited by the bfs/dfs in the residual graph might be useful for others. – Hyetology

For those who are struggling to figure out why visiting in residual graph is different than just following residual edges: The saturated edges does not mean path is blocked because there might be flow coming from opposite direction that cancels out. – Gironde

What is bfs and dfs? – Woodham

@Woodham (bfs) breadth first search and (dfs) depth first search are graph traversal algorithms. Have a look at en.wikipedia.org/wiki/Depth-first_search and en.wikipedia.org/wiki/Breadth-first_search – Leund

@Leund I doubt the correctness of the algorithm. Is it possible to provide a proof or I am missing something? I think the algorithm fails at this example imgur.com/a/ycTVsyv, with a max-flow of 20. – Telegenic

@Telegenic I think there is an issue with your maxflow and therefore also with your residual network. The edge between the middle and the top vertex has capacity 10 downwards and 0 upwards. That means in the original undirected graph this edge has capacity 10. But then the maxflow algo could still push 5 more flow from source to sink through this edge. hth – Leund

Answer 3

So, to give the exact procedure how to obtain the minimum cut:

1. Run Ford-Fulkerson algorithm to find the max flow and to get the residual graph¹.
2. Run BFS on the residual graph to find the set of vertices that are reachable from source in the residual graph (respecting that you can't use edges with 0 capacity in the residual graph). IMPORTANT: You have to use reverse edges in the residual graph to find the correct set of reachable vertices!!! (See this algorithm)
3. All edges in the original graph which are from a reachable vertex to non-reachable vertex are minimum cut edges. Print all such edges.

¹ Graph in which the capacity of an edge is defined like it's original capacity minus its flow (flow from the maximum flow network).

Frendel

Thanks for formulation "which are from a reachable vertex to non-reachable vertex". – Calva

Answer 4

Note: Falk's algorythm can be used to find both a minimum cut with minimum vertices and with maximum vertices. For the latter the algorythm should be reversed, ie. search from the sink vertex instead of the source. See a related question: Network Flow: Adding a new edge

Doyon

Answer 5

After the maximum flow is calculated, we can search for edges (u,v) such that in the residual graph, there's a edge in the residual graph from v to u and f(v,u) = c(u,v) [which means the edge is saturated]

After shortlisting such edges, we can select such edges (u,v) by using the criteria that there exists no path from u to sink t in the residual graph. If this condition is satisfied, then such edges form a part of (S,T) cut

Running time of this algorithm may be O(E) * O( V + E ) = O( E^2 )

Obscurant

Answer 6

I think this is what other people are saying, but I found it unclear so here's my explanation:

From the source node, do a flood fill of the graph, travelling only along edges with residual capacity, marking each visited vertex. You can use a DFS for this. Recall that back edges from a vertex have a residual capacity - equal to the flow along the forward edge (ie. r(u, v) = remaining capacity for edge (u, v), r(v, u) = flow(u, v)).

In effect, this determines the S part of the S-T cut of the graph.

The minimum cut will now be the set of edges such that one vertex is marked from your flood fill above, and the other vertex is not marked. These will be edges without residual capacity (otherwise you would have traversed them in your DFS), and together form the minimum cut.

After removing these edges, the set of unmarked vertices will form the T section of the cut.

Homogeneous

Answer 7

One way to understand is, let's define a cut as two sets S and T, which will include s and t, respectively.

Now, add all vertices in S that are reachable from s in the residual network and put the remaining edges in T. This will be one cut.

Second, cut can be formed by putting all vertices in T that are reachable from t in the residual network and put the remaining vertices in S.

Take a look at this video to find out how do we find the vertices reachable from s and t.

https://www.youtube.com/watch?v=FIJaXfUIXJA&index=4&list=PLe-ggMe31CTduQ68XQ-sVj32wYJIspTma

Tenne