What does (number & -number) mean in bit programming? [duplicate]

Question

For example:

int get(int i) {
    int res = 0;
    while (i) {
        res = (res + tree[i]) % MOD;
        i -= ( (i) & (-i) );
    }
    return res;
}

A tree update function:

void update(int i, int val) {
    while (i <= m) {
        tree[i] = (tree[i] + val) % MOD;
        i += ( (i) & (-i) );
    }
}

Can you please explain what they do in the code by using ( (i) & (-i) )?

Photoflash

i & (-i) is the lowest bit that is set (i.e. rightmost 1). – Zofiazoha

And if you want to see how it works, consider the twos-complement of a signed number n (used to represent -n) and what happens if you and it with n. – Equanimous

ow.. now i can understand. Thanks for your help. :) – Photoflash

Don't expect to invent hacks like that on your own. These ideas are copied far more often than they're invented. – Ai

Enjoy more hacks: Level Easy and Level Hard – Phenanthrene

The standard reference for bithacks is: graphics.stanford.edu/~seander/bithacks.html , but yours is not listed there. – Teetotum

@Phenanthrene - The first link is specifically dealing with Javascript. While the code is similar and the same tricks can be used, I'm not sure how much benefit there would be. A decent C++ compiler would perform many of those optimizations anyhow. I'd be interested to see a speed comparison for using those tricks in C++. – Keynesianism

@DarrelHoffman ActionScript, not JS, but bits are bits anyway. BitHacks in that post are actually copied from more descriptive Article about C - which does not seem to have anything over "Level Hard". If you want to check out speed try BitHackAbsolute() (at larger dataset of course), its is fast because it removes branch but does it at cost of potential issues with Min Value - which leads to optimizer not using it. – Phenanthrene

Related is the question: 2*b | ~(2*b). – Versieversification

Good practice would have recommended putting hacks of this kind in an inline function with a self-documenting name such as least_significant_bit_set. – Plumage

see also Why is “i & (i ^ (i - 1))” equivalent to “i & (-i)” – Gumm

Answer 1

This two functions are a modified implementation of a Binary index tree (Fenwick tree) data structure.
Here is two pictures to supplement MikeCAT's answer showing how i variable updates for different values.

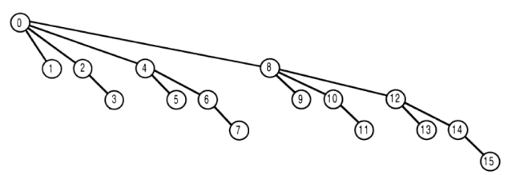
The "get" function:
For assume max value in of input in function is 15 for simplicity of representation.

A node with number t in on it represents tree[t] in the tree array.
If you call get function for i the returned value is sum of tree[i] plus sum of all tree array elements that their index in the array is a parent of i in the picture, except zero.
Here are some examples:

get(15) = tree[15] + tree[14] + tree[12] + tree[8]
get(14) = tree[14] + tree[12] + tree[8]
get(13) = tree[13] + tree[12] + tree[8]
get(12) = tree[12] + tree[8]
get(11) = tree[11] + tree[10] + tree[8]
get(10) = tree[10] + tree[8]
get(9) = tree[9] + tree[8]
get(8) = tree[8]
get(7) = tree[7] + tree[6] + tree[4]
get(6) = tree[6] + tree[4]
get(5) = tree[5] + tree[4]
get(4) = tree[4]
get(3) = tree[3] + tree[2]
get(2) = tree[2]

Numbers on the labels on nodes in the above picture has the property that each node's parent is that node label minus the least significant one 1(explained very well on @MikeCAT answer)
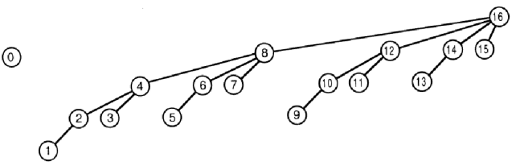
The "update" function:
For simplicity of picture, let assume that the max length of the tree array is 16.
The update function is little bit trickier.

It adds val to tree[i] and all tree elements that their index is parent of the node with label i in the picture.

update(16, val) --> tree[16] += val;
update(15, val) --> tree[15] += val, tree[16] += val;
update(14, val) --> tree[14] += val, tree[16] += val;
update(13, val) --> tree[13] += val, tree[14] += val; tree[16] += val;
update(12, val) --> tree[12] += val, tree[16] += val;
update(11, val) --> tree[11] += val, tree[12] += val, tree[16] += val;
update(10, val) --> tree[10] += val, tree[12] += val, tree[16] += val;
update(9, val)  --> tree[9] += val, tree[10] += val, tree[12] += val, tree[16] += val;
update(8, val)  --> tree[8] += val, tree[16] += val;
update(7, val)  --> tree[7] += val, tree[8] += val, tree[16] += val;
update(6, val)  --> tree[6] += val, tree[8] += val, tree[16] += val;
update(5, val)  --> tree[5] += val, tree[6] += val, tree[8] += val, tree[16] += val;
update(4, val)  --> tree[4] += val, tree[8] += val, tree[16] += val;
update(3, val)  --> tree[3] += val, tree[4] += val, tree[8] += val, tree[16] += val;
update(2, val)  --> tree[2] += val, tree[4] += val, tree[8] += val, tree[16] += val;
update(1, val)  --> tree[1] += val, tree[2] += val, tree[4] += val, tree[8] += val, tree[16] += val;

Samara

Answer 2

Let me assume that negative value is represented using two's complement. In this case, -i can be calculated as (~i)+1 (flip bits, then add 1).

For example, let me consider i = 44. Then, in binary,

i           = 0000 0000 0000 0000 0000 0000 0010 1100
~i          = 1111 1111 1111 1111 1111 1111 1101 0011
-i = (~i)+1 = 1111 1111 1111 1111 1111 1111 1101 0100
(i) & (-i)  = 0000 0000 0000 0000 0000 0000 0000 0100

As you see, the least bit that is 1 can be calculated using (i) & (-i).

Neural

thanks for your explain. now i totally understand :) – Photoflash

Wouldn't this be implementation-dependent? I would guess all current compilers use two's complement for negative numbers, but nobody stops a compiler or architecture from doing it differently, which might lead to undefined behavior. – Hegarty

@vsz: The C standard explicitly allows for that, and in fact, signed integers can have trap representations (like negative zero), so this is well into UB land. Of course, -i is already potential UB since i could be the most negative integer, giving you signed integer overflow (which is also undefined). – Moving

For working code sample see: https://mcmap.net/q/297516/-meaning-of-number-amp-number – Cairn

Answer 3

In case anyone wanted a more general proof as well,

Assume x has the format a10^k (meaning here, some bitstring a, followed by a 1, followed by k zeroes).

-x is (by definition) the same thing as ~x + 1, so

• x & -x = (fill in)
• a10^k & -(a10^k) = (def. of negation)
• a10^k & ~(a10^k) + 1 = (apply inversion)
• a10^k & ~a01^k + 1 = (add 1)
• a10^k & ~a10^k = (AND between something and its inverse)
• 0^w10^k

So we are left with only that single rightmost 1 that we assumed existed.

The assumption about the form of x leaves out the case that x = 0, in which case the result is obviously still zero.

Ilona