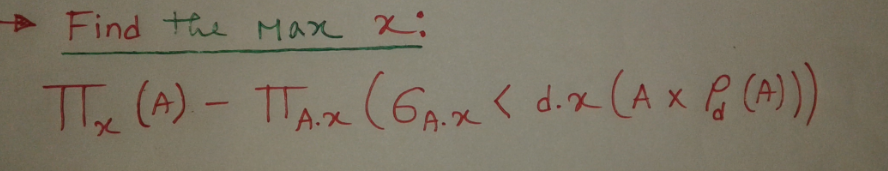How can I find MAX with relational algebra?

Question

Working with databases, how can I find MAX using relational algebra?

Groscr

Aggregate Relational Algebra (Maximum) – Gills

Answer 1

Assuming you have a relation, A, with a single attribute, 'a' (reducing a more complex relation to this is a simple task in relational algebra, I'm sure you got this far), so now you want to find the maximum value in A.

One way to do it is to find the cross product of A with itself, be sure to rename 'a' so your new relation has attributes with distinct names. for example:

(rename 'a' as 'a1') X (rename 'a' as 'a2')

now select 'a1' < 'a2', the resulting relation will have all values except the maximum. To get the max simply find the difference between your original relation:

(A x A) - (select 'a1' < 'a2') ((rename 'a' as 'a1')(A) x (rename 'a' as 'a2')(A))

Then use the project operator to reduce down to a single column as Tobi Lehman suggests in the comment below.

Writing this in relational algebra notation would be (if I remember correctly). Note the final rename (i.e. ρ) is just to end up with an attribute that has the same name as in the original relation:

ρ_a/a1(π_a1((A x A) - σ_{a1 < a2} (ρ_a1/a(A) x ρ_a2/a(A))))

Aparicio

Just a small nit pick, but the set difference expression A-(...) should be (AxA - (...)), since the right hand set is full of pairs. Then, after subtracting all of the pairs, use the projection operator to extract it. – Yearwood

This answer is only partly right. Firstly, I don't believe A x A is well defined since A and A have attributes in common (obviously since they have the same schemas) and a relation can't have duplicate attributes. You note this yourself, and I suppose you've just forgotten to perform the same renaming on the left cartesian product as on the right. – Bourgogne

Furthermore, you take the difference of the cartesian product of A with itself, and all of the tuples from the cartesian product of A with itself where a1 < a2. This results in a relation where a1 >= a2. Finally, you project onto a1 and rename a1 to a, leaving you with the same instance of relation A as the one you began with. I'm clueless as to why this answer has got this many upvotes without being corrected, is my reasoning maybe faulty? The last part of @idipous answer is the correct answer to the question. – Bourgogne

@gblomqvist yeah you're right, I looked through the edit history and originally just had A - ... and a comment saying you still need to project but then I changed it based on tlehman's comment above. idipous's answer is more complete – Aparicio

This is wrong because you didn't project out a2 before subtracting it from A x A – Muscarine

Answer 2

Just my two cents as I was trying to solve this today myself.

Lets say we have A = 1,2,3

If you use

A x A - (select 'a1' < 'a2') ((rename 'a' as 'a1')(A) x (rename 'a' as 'a2')(A))

you will not get the single max value rather two columns like 1|1, 2|1,3|2,3|1,3|2,3|3

the way to get just 3 is

project(a)A - project(a1)((select 'a1' < 'a2') ((rename 'a' as 'a1')(A) x (rename 'a' as 'a2')(A)))

At least that is what I had to do in a similar situation.

Hope it helps someone

Cherianne

Answer 3

lets think we have a relation with an attribute A and values 1,2,3

A

1
2
3

so now..

project A values and rename with A1

A1
1
2
3

again project A values and rename with A2

A2
1
2
3

join this with A2<A1 i.e \join_{A2<A1}
so the - Output schema: (A2 integer, A1 integer)

A2<A1

1|2
1|3
2|3

hear always A2 values will be less than A1 because we join like that(a2<a1)

now project A2 the output is like below

A2
1
2

now diff with original attribute

A diff A2

A
1
2
3

 diff

A2
1
2

Output is 3 maximum value

Merylmes

Answer 4

I've forgotten most of the relational algebra syntax now. A query just using SELECT, PROJECT, MINUS and RENAME would be

SELECT v1.number
FROM values v1
MINUS
SELECT v1.number
FROM values v1 JOIN values v2 ON v2.number > v1.number

Hopefully you can translate!

Shaylyn

Answer 5

I know this is old, but here is a hand-written formula which might be handy!

Relation A: 1,2,3,4

1. First we want to PROJECT and RENAME relation A
2. We then to a THETA JOIN with the test a1<a2
3. We then PROJECT the result of the relation to give us a single set of values 
   a1: 1,2,3 (not max value since a1<a2)

4. We then apply the difference operator with the original relation so: 
   1,2,3,4 --- 1,2,3 returns 4

   4 is the Max value.

Maclay

@gudthing The think the formula has a mistake in the sense that the two expressions around the - operator should change their position. the difference of r1(X) and r2(X) is expressed as r1 − r2 and is a relation on X containing the tuples that belong to r1 and not to r2 – Hexahedron

Please use text, not images/links, for text (including code, tables & ERDs). Use an image only for convenience to supplement text and/or for what cannot be given in text. And never give a diagram without a legend/key. Use edit functions to inline, not links, if you have the rep--make your post self-contained. – Gills

Answer 6

Find the MAX:

• Strategy:

  1. Find those x that are not the MAX.

     • Rename A relation as d so that we can compare each A x with all others.

  2. Use set difference to find those A x that were not found in the earlier step.

• The query is:

Bluebird

Suppose A had another column y, and you were asked to select y with max x, how would you do that? Thanks. – Goodish

Please use text, not images/links, for text (including code, tables & ERDs). Use an image only for convenience to supplement text and/or for what cannot be given in text. And never give a diagram without a legend/key. Use edit functions to inline, not links, if you have the rep--make your post self-contained. – Gills

Answer 7

 Project x(A) - Project A.x
(Select A.x < d.x (A x Rename d(A)))

Velodrome

Answer 8

Relational Algebra (Filtering through Comparison)

Recently had this question turn up as practice material in a Database module and when I was searching around for help I couldn't find any good answers. The answer by "Md. Rezwanul Haque" is correct but it's not really explained as it relies on prior knowledge (If you don't understand Cartesian Product that is).

So, here is the answer with my explanation hopefully this makes it easier for some:

    TABLE: PEOPLE
PEOPLE.name PEOPLE.age
'Jack'      16
'Megan'     15
'Harry'     14
'Lilly'     16
'Michael'   8

The idea is to "Collect what you don't want and remove it from what you have; leaving you with what you want."

Step 1 (Building a Table to Query)

When filtering using SELECTION we can only compare what is in the Tuple we have. This means we need to add to those tuples the data we want to compare it to.

So, we would need to merge our PEOPLE Table with the data we want to compare with. This can be done using the x (Cartesian Product) Operator

Something like this: PEOPLE x PEOPLE however we cannot do this as the resulting table would look something like this:

           TABLE: PEOPLE x PEOPLE
PEOPLE.name PEOPLE.age PEOPLE.name PEOPLE.age 
'Jack'      16         'Jack'      16

We have duplicate Attribute names this means that we need to create a Copy of the PEOPLE Table, one which has a different name that we can reference. Otherwise we cannot use the x Cartesian Product Operator as it requires that all attributes be unique in the resulting table, you can not have two PEOPLE.name attributes.

This is where we would use the RENAME Operator which would look something like this:

PEOPLE ⨯ (ρ ALT (PEOPLE))

Here what I've done is use the Cartesian Product to merge PEOPLE and ALT where ALT is PEOPLE renamed to ALT

This would give us a Table that looks a bit like this:

          TABLE: PEOPLE x ALT
PEOPLE.name  PEOPLE.age ALT.name  ALT.age
'jack'       16         'jack'    16
'jack'       16         'megan'   15
'jack'       16         'harry'   14
'jack'       16         'lilly'   16
'jack'       16         'michael' 8

(The resulting table is (PEOPLE.size * PEOPLE.size) = 5*5 where size is the number of tuples) Where every value of PEOPLE is put against every value of ALT

Step 2 (Selecting)

Now we can filter through all values and grab the ones we don't want. So let's say I only want the eldest people in PEOPLE this question can be reworded to: Only people who are not younger than someone so we grab only those who are younger than someone. We do this because it's easier to Query for what we don't want that what we do want.

So, our Predicate would be: PEOPLE.age < ALT.age where we are selecting only those who are younger than someone.

If we were to reverse the Predicate to PEOPLE.age > ALT.age we would get a mix of people who are not the eldest, but who are older than at least one person. This could help us obtain the person who is the youngest

Giving us a SELECTION like this:

(σ (PEOPLE.age < ALT.age) (PEOPLE x (ρ ALT (PEOPLE))))

This would produce a TABLE like this:

TABLE: (σ (PEOPLE.age < ALT.age) (PEOPLE x (ρ ALT (PEOPLE))))

PEOPLE.age  PEOPLE.name  ALT.name  ALT.age 
'megan'     15           'jack'    16
'megan'     15           'lilly'   16
'harry'     14           'jack'    16
'harry'     14           'megan'   15
'harry'     14           'lilly'   16
'michael'   8            'jack'    16
'michael'   8            'megan'   15
'michael'   8            'harry'   14
'michael'   8            'lilly'   16

Where the results are people who are younger than someone, and who they're younger than. However our Query is: Only people who are not younger than someone which is the exact opposite of this. So this isn't our goal, we need to do a little bit more. If you were to do:

π PEOPLE.name PEOPLE.age (σ (PEOPLE.age < ALT.age) (PEOPLE x (ρ ALT (PEOPLE))))

This would give us a table consisting of megan, harry, and michael this is a table consisting of: Only people who are younger than someone

Step 3 (Getting our final Table)

Now we have a Table that consists of Only people who are younger than someone but what we want is Only people who are not younger than someone so what we need to do is remove all of the people who are younger than someone from the PEOPLE Table to give us only those who are not younger than someone.

So we need to use the Subtraction Operation to remove those Tuples from our PEOPLE table. Which gives us our Final Query of:

PEOPLE - (π PEOPLE.name PEOPLE.age (σ (PEOPLE.age < ALT.age) (PEOPLE x (ρ ALT (PEOPLE)))))

Which produces the following Table:

PEOPLE - (π PEOPLE.name PEOPLE.age (σ (PEOPLE.age < ALT.age) (PEOPLE x (ρ ALT (PEOPLE)))))

PEOPLE.name PEOPLE.age
'jack'      16
'lilly'     16

Where Jack and Lilly are the only people in PEOPLE who are NOT Younger than someone.

Flap