My input is a list of lists. Some of them share common elements, eg.
L = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
I need to merge all lists, that share a common element, and repeat this procedure as long as there are no more lists with the same item. I thought about using boolean operations and a while loop, but couldn't come up with a good solution.
The final result should be:
L = [['a','b','c','d','e','f','g','o','p'],['k']]
You can see your list as a notation for a Graph, ie ['a','b','c'] is a graph with 3 nodes connected to each other. The problem you are trying to solve is finding connected components in this graph.
You can use NetworkX for this, which has the advantage that it's pretty much guaranteed to be correct:
l = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
import networkx
from networkx.algorithms.components.connected import connected_components
def to_graph(l):
G = networkx.Graph()
for part in l:
# each sublist is a bunch of nodes
G.add_nodes_from(part)
# it also imlies a number of edges:
G.add_edges_from(to_edges(part))
return G
def to_edges(l):
"""
treat `l` as a Graph and returns it's edges
to_edges(['a','b','c','d']) -> [(a,b), (b,c),(c,d)]
"""
it = iter(l)
last = next(it)
for current in it:
yield last, current
last = current
G = to_graph(l)
print connected_components(G)
# prints [['a', 'c', 'b', 'e', 'd', 'g', 'f', 'o', 'p'], ['k']]
To solve this efficiently yourself you have to convert the list into something graph-ish anyways, so you might as well use networkX from the start.
to_edges function could be replaced by izip(part[:-1], part[1:]). –
Skitter Algorithm:
So you might want to use sets instead of list. The following program should do it.
l = [['a', 'b', 'c'], ['b', 'd', 'e'], ['k'], ['o', 'p'], ['e', 'f'], ['p', 'a'], ['d', 'g']]
out = []
while len(l)>0:
first, *rest = l
first = set(first)
lf = -1
while len(first)>lf:
lf = len(first)
rest2 = []
for r in rest:
if len(first.intersection(set(r)))>0:
first |= set(r)
else:
rest2.append(r)
rest = rest2
out.append(first)
l = rest
print(out)
first, *rest = l construct is Python 3 only, swapping it with first, rest = l[0], l[1:] seems to work fine on python 2.7 –
Banjermasin I needed to perform the clustering technique described by the OP millions of times for rather large lists, and therefore wanted to determine which of the methods suggested above is both most accurate and most performant.
I ran 10 trials for input lists sized from 2^1 through 2^10 for each method above, using the same input list for each method, and measured the average runtime for each algorithm proposed above in milliseconds. Here are the results:
These results helped me see that of the methods that consistently return correct results, @jochen's is the fastest. Among those methods that don't consistently return correct results, mak's solution often does not include all of the input elements (i.e. list of list members are missing), and the solutions of braaksma, cmangla, and asterisk are not guaranteed to be maximally merged.
It's interesting that the two fastest, correct algorithms have the top two amount of upvotes to date, in properly ranked order.
Here's the code used to run the tests:
from networkx.algorithms.components.connected import connected_components
from itertools import chain
from random import randint, random
from collections import defaultdict, deque
from copy import deepcopy
from multiprocessing import Pool
import networkx
import datetime
import os
##
# @mimomu
##
def mimomu(l):
l = deepcopy(l)
s = set(chain.from_iterable(l))
for i in s:
components = [x for x in l if i in x]
for j in components:
l.remove(j)
l += [list(set(chain.from_iterable(components)))]
return l
##
# @Howard
##
def howard(l):
out = []
while len(l)>0:
first, *rest = l
first = set(first)
lf = -1
while len(first)>lf:
lf = len(first)
rest2 = []
for r in rest:
if len(first.intersection(set(r)))>0:
first |= set(r)
else:
rest2.append(r)
rest = rest2
out.append(first)
l = rest
return out
##
# Nx @Jochen Ritzel
##
def jochen(l):
l = deepcopy(l)
def to_graph(l):
G = networkx.Graph()
for part in l:
# each sublist is a bunch of nodes
G.add_nodes_from(part)
# it also imlies a number of edges:
G.add_edges_from(to_edges(part))
return G
def to_edges(l):
"""
treat `l` as a Graph and returns it's edges
to_edges(['a','b','c','d']) -> [(a,b), (b,c),(c,d)]
"""
it = iter(l)
last = next(it)
for current in it:
yield last, current
last = current
G = to_graph(l)
return list(connected_components(G))
##
# Merge all @MAK
##
def mak(l):
l = deepcopy(l)
taken=[False]*len(l)
l=map(set,l)
def dfs(node,index):
taken[index]=True
ret=node
for i,item in enumerate(l):
if not taken[i] and not ret.isdisjoint(item):
ret.update(dfs(item,i))
return ret
def merge_all():
ret=[]
for i,node in enumerate(l):
if not taken[i]:
ret.append(list(dfs(node,i)))
return ret
result = list(merge_all())
return result
##
# @cmangla
##
def cmangla(l):
l = deepcopy(l)
len_l = len(l)
i = 0
while i < (len_l - 1):
for j in range(i + 1, len_l):
# i,j iterate over all pairs of l's elements including new
# elements from merged pairs. We use len_l because len(l)
# may change as we iterate
i_set = set(l[i])
j_set = set(l[j])
if len(i_set.intersection(j_set)) > 0:
# Remove these two from list
l.pop(j)
l.pop(i)
# Merge them and append to the orig. list
ij_union = list(i_set.union(j_set))
l.append(ij_union)
# len(l) has changed
len_l -= 1
# adjust 'i' because elements shifted
i -= 1
# abort inner loop, continue with next l[i]
break
i += 1
return l
##
# @pillmuncher
##
def pillmuncher(l):
l = deepcopy(l)
def connected_components(lists):
neighbors = defaultdict(set)
seen = set()
for each in lists:
for item in each:
neighbors[item].update(each)
def component(node, neighbors=neighbors, seen=seen, see=seen.add):
nodes = set([node])
next_node = nodes.pop
while nodes:
node = next_node()
see(node)
nodes |= neighbors[node] - seen
yield node
for node in neighbors:
if node not in seen:
yield sorted(component(node))
return list(connected_components(l))
##
# @NicholasBraaksma
##
def braaksma(l):
l = deepcopy(l)
lists = sorted([sorted(x) for x in l]) #Sorts lists in place so you dont miss things. Trust me, needs to be done.
resultslist = [] #Create the empty result list.
if len(lists) >= 1: # If your list is empty then you dont need to do anything.
resultlist = [lists[0]] #Add the first item to your resultset
if len(lists) > 1: #If there is only one list in your list then you dont need to do anything.
for l in lists[1:]: #Loop through lists starting at list 1
listset = set(l) #Turn you list into a set
merged = False #Trigger
for index in range(len(resultlist)): #Use indexes of the list for speed.
rset = set(resultlist[index]) #Get list from you resultset as a set
if len(listset & rset) != 0: #If listset and rset have a common value then the len will be greater than 1
resultlist[index] = list(listset | rset) #Update the resultlist with the updated union of listset and rset
merged = True #Turn trigger to True
break #Because you found a match there is no need to continue the for loop.
if not merged: #If there was no match then add the list to the resultset, so it doesnt get left out.
resultlist.append(l)
return resultlist
##
# @Rumple Stiltskin
##
def stiltskin(l):
l = deepcopy(l)
hashdict = defaultdict(int)
def hashit(x, y):
for i in y: x[i] += 1
return x
def merge(x, y):
sums = sum([hashdict[i] for i in y])
if sums > len(y):
x[0] = x[0].union(y)
else:
x[1] = x[1].union(y)
return x
hashdict = reduce(hashit, l, hashdict)
sets = reduce(merge, l, [set(),set()])
return list(sets)
##
# @Asterisk
##
def asterisk(l):
l = deepcopy(l)
results = {}
for sm in ['min', 'max']:
sort_method = min if sm == 'min' else max
l = sorted(l, key=lambda x:sort_method(x))
queue = deque(l)
grouped = []
while len(queue) >= 2:
l1 = queue.popleft()
l2 = queue.popleft()
s1 = set(l1)
s2 = set(l2)
if s1 & s2:
queue.appendleft(s1 | s2)
else:
grouped.append(s1)
queue.appendleft(s2)
if queue:
grouped.append(queue.pop())
results[sm] = grouped
if len(results['min']) < len(results['max']):
return results['min']
return results['max']
##
# Validate no more clusters can be merged
##
def validate(output, L):
# validate all sublists are maximally merged
d = defaultdict(list)
for idx, i in enumerate(output):
for j in i:
d[j].append(i)
if any([len(i) > 1 for i in d.values()]):
return 'not maximally merged'
# validate all items in L are accounted for
all_items = set(chain.from_iterable(L))
accounted_items = set(chain.from_iterable(output))
if all_items != accounted_items:
return 'missing items'
# validate results are good
return 'true'
##
# Timers
##
def time(func, L):
start = datetime.datetime.now()
result = func(L)
delta = datetime.datetime.now() - start
return result, delta
##
# Function runner
##
def run_func(args):
func, L, input_size = args
results, elapsed = time(func, L)
validation_result = validate(results, L)
return func.__name__, input_size, elapsed, validation_result
##
# Main
##
all_results = defaultdict(lambda: defaultdict(list))
funcs = [mimomu, howard, jochen, mak, cmangla, braaksma, asterisk]
args = []
for trial in range(10):
for s in range(10):
input_size = 2**s
# get some random inputs to use for all trials at this size
L = []
for i in range(input_size):
sublist = []
for j in range(randint(5, 10)):
sublist.append(randint(0, 2**24))
L.append(sublist)
for i in funcs:
args.append([i, L, input_size])
pool = Pool()
for result in pool.imap(run_func, args):
func_name, input_size, elapsed, validation_result = result
all_results[func_name][input_size].append({
'time': elapsed,
'validation': validation_result,
})
# show the running time for the function at this input size
print(input_size, func_name, elapsed, validation_result)
pool.close()
pool.join()
# write the average of time trials at each size for each function
with open('times.tsv', 'w') as out:
for func in all_results:
validations = [i['validation'] for j in all_results[func] for i in all_results[func][j]]
linetype = 'incorrect results' if any([i != 'true' for i in validations]) else 'correct results'
for input_size in all_results[func]:
all_times = [i['time'].microseconds for i in all_results[func][input_size]]
avg_time = sum(all_times) / len(all_times)
out.write(func + '\t' + str(input_size) + '\t' + \
str(avg_time) + '\t' + linetype + '\n')
And for plotting:
library(ggplot2)
df <- read.table('times.tsv', sep='\t')
p <- ggplot(df, aes(x=V2, y=V3, color=as.factor(V1))) +
geom_line() +
xlab('number of input lists') +
ylab('runtime (ms)') +
labs(color='') +
scale_x_continuous(trans='log10') +
facet_wrap(~V4, ncol=1)
ggsave('runtimes.png')
I came across the same issue of trying to merge down lists with common values. This example may be what you are looking for. It only loops over lists once and updates resultset as it goes.
lists = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
lists = sorted([sorted(x) for x in lists]) #Sorts lists in place so you dont miss things. Trust me, needs to be done.
resultslist = [] #Create the empty result list.
if len(lists) >= 1: # If your list is empty then you dont need to do anything.
resultlist = [lists[0]] #Add the first item to your resultset
if len(lists) > 1: #If there is only one list in your list then you dont need to do anything.
for l in lists[1:]: #Loop through lists starting at list 1
listset = set(l) #Turn you list into a set
merged = False #Trigger
for index in range(len(resultlist)): #Use indexes of the list for speed.
rset = set(resultlist[index]) #Get list from you resultset as a set
if len(listset & rset) != 0: #If listset and rset have a common value then the len will be greater than 1
resultlist[index] = list(listset | rset) #Update the resultlist with the updated union of listset and rset
merged = True #Turn trigger to True
break #Because you found a match there is no need to continue the for loop.
if not merged: #If there was no match then add the list to the resultset, so it doesnt get left out.
resultlist.append(l)
print resultlist
resultset = [['a', 'b', 'c', 'd', 'e', 'g', 'f', 'o', 'p'], ['k']]
I think this can be solved by modelling the problem as a graph. Each sublist is a node and shares an edge with another node only if the two sublists have some element in common. Thus, a merged sublist is basically a connected component in the graph. Merging all of them is simply a matter of finding all connected components and listing them.
This can be done by a simple traversal over the graph. Both BFS and DFS can be used, but I'm using DFS here since it is somewhat shorter for me.
l = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
taken=[False]*len(l)
l=[set(elem) for elem in l]
def dfs(node,index):
taken[index]=True
ret=node
for i,item in enumerate(l):
if not taken[i] and not ret.isdisjoint(item):
ret.update(dfs(item,i))
return ret
def merge_all():
ret=[]
for i,node in enumerate(l):
if not taken[i]:
ret.append(list(dfs(node,i)))
return ret
print(merge_all())
L = [['a','b','c','d','e','f','g','o','p'],['k']] but in 3.5.3 this code prints [['a', 'c', 'b', 'p']]. Perhaps I'm missing something? My post above runs random tests with different inputs, so you could check that too... –
Supercool I have found itertools a fast option for merging lists and it solved this problem for me:
import itertools
LL = set(itertools.chain.from_iterable(L))
# LL is {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'k', 'o', 'p'}
for each in LL:
components = [x for x in L if each in x]
for i in components:
L.remove(i)
L += [list(set(itertools.chain.from_iterable(components)))]
# then L = [['k'], ['a', 'c', 'b', 'e', 'd', 'g', 'f', 'o', 'p']]
For large sets sorting LL by frequency from the most common elements to the least can speed things up a bit
As Jochen Ritzel pointed out you are looking for connected components in a graph. Here is how you could implement it without using a graph library:
from collections import defaultdict
def connected_components(lists):
neighbors = defaultdict(set)
seen = set()
for each in lists:
for item in each:
neighbors[item].update(each)
def component(node, neighbors=neighbors, seen=seen, see=seen.add):
nodes = set([node])
next_node = nodes.pop
while nodes:
node = next_node()
see(node)
nodes |= neighbors[node] - seen
yield node
for node in neighbors:
if node not in seen:
yield sorted(component(node))
L = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
print list(connected_components(L))
You can use networkx library because is a graph theory and connected components problem:
import networkx as nx
L = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
G = nx.Graph()
#Add nodes to Graph
G.add_nodes_from(sum(L, []))
#Create edges from list of nodes
q = [[(s[i],s[i+1]) for i in range(len(s)-1)] for s in L]
for i in q:
#Add edges to Graph
G.add_edges_from(i)
#Find all connnected components in graph and list nodes for each component
[list(i) for i in nx.connected_components(G)]
Output:
[['p', 'c', 'f', 'g', 'o', 'a', 'd', 'b', 'e'], ['k']]
I miss a non quirurgic version. I post it on 2018 (7 years later)
An easy and understable approach:
1) make cartesian product ( cross join ) merging both if elements in common
2) remove dups
#your list
l=[['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
#import itertools
from itertools import product, groupby
#inner lists to sets (to list of sets)
l=[set(x) for x in l]
#cartesian product merging elements if some element in common
for a,b in product(l,l):
if a.intersection( b ):
a.update(b)
b.update(a)
#back to list of lists
l = sorted( [sorted(list(x)) for x in l])
#remove dups
list(l for l,_ in groupby(l))
#result
[['a', 'b', 'c', 'd', 'e', 'f', 'g', 'o', 'p'], ['k']]
My attempt. Has functional look to it.
#!/usr/bin/python
from collections import defaultdict
l = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']]
hashdict = defaultdict(int)
def hashit(x, y):
for i in y: x[i] += 1
return x
def merge(x, y):
sums = sum([hashdict[i] for i in y])
if sums > len(y):
x[0] = x[0].union(y)
else:
x[1] = x[1].union(y)
return x
hashdict = reduce(hashit, l, hashdict)
sets = reduce(merge, l, [set(),set()])
print [list(sets[0]), list(sets[1])]
This is a fairly fast solution with no dependencies. It works as follows:
Assign a unique reference number to each of your subsists (in this case, the initial index of the sublist)
Create a dictionary of the reference elements for each sublist, and for each item in each sublist.
Repeat the following procedure until it causes no changes:
3a. Go through each item in each sublist. If that item's current reference number is different from the reference number of its sublist, then the element must be part of two lists. Merge the two lists (removing the current sublist from the reference) and set the reference number of all items in the current sublist to be the reference number of the new sublist.
When this procedure causes no changes, it is because all elements are part of exactly one list. Since working set is decreasing in size on every iteration, the algorithm necessarily terminates.
def merge_overlapping_sublists(lst):
output, refs = {}, {}
for index, sublist in enumerate(lst):
output[index] = set(sublist)
for elem in sublist:
refs[elem] = index
changes = True
while changes:
changes = False
for ref_num, sublist in list(output.items()):
for elem in sublist:
current_ref_num = refs[elem]
if current_ref_num != ref_num:
changes = True
output[current_ref_num] |= sublist
for elem2 in sublist:
refs[elem2] = current_ref_num
output.pop(ref_num)
break
return list(output.values())
Here are a set of tests for this code:
def compare(a, b):
a = list(b)
try:
for elem in a:
b.remove(elem)
except ValueError:
return False
return not b
import random
lst = [["a", "b"], ["b", "c"], ["c", "d"], ["d", "e"]]
random.shuffle(lst)
assert compare(merge_overlapping_sublists(lst), [{"a", "b", "c", "d", "e"}])
lst = [["a", "b"], ["b", "c"], ["f", "d"], ["d", "e"]]
random.shuffle(lst)
assert compare(merge_overlapping_sublists(lst), [{"a", "b", "c",}, {"d", "e", "f"}])
lst = [["a", "b"], ["k", "c"], ["f", "g"], ["d", "e"]]
random.shuffle(lst)
assert compare(merge_overlapping_sublists(lst), [{"a", "b"}, {"k", "c"}, {"f", "g"}, {"d", "e"}])
lst = [["a", "b", "c"], ["b", "d", "e"], ["k"], ["o", "p"], ["e", "f"], ["p", "a"], ["d", "g"]]
random.shuffle(lst)
assert compare(merge_overlapping_sublists(lst), [{"k"}, {"a", "c", "b", "e", "d", "g", "f", "o", "p"}])
lst = [["a", "b"], ["b", "c"], ["a"], ["a"], ["b"]]
random.shuffle(lst)
assert compare(merge_overlapping_sublists(lst), [{"a", "b", "c"}])
Note that the return value is a list of sets.
Without knowing quite what you want, I decided to just guess you meant: I want to find every element just once.
#!/usr/bin/python
def clink(l, acc):
for sub in l:
if sub.__class__ == list:
clink(sub, acc)
else:
acc[sub]=1
def clunk(l):
acc = {}
clink(l, acc)
print acc.keys()
l = [['a', 'b', 'c'], ['b', 'd', 'e'], ['k'], ['o', 'p'], ['e', 'f'], ['p', 'a'], ['d', 'g']]
clunk(l)
Output looks like:
['a', 'c', 'b', 'e', 'd', 'g', 'f', 'k', 'o', 'p']
.__class__ == list looks so incredibly wrong. At the very least, isinstance(sub, list). If only as a matter of principle. (Also, you could/should just use a set instead of a dict with bogus values.) –
Babbette This is perhaps a simpler/faster algorithm and seems to work well -
l = [['a', 'b', 'c'], ['b', 'd', 'e'], ['k'], ['o', 'p'], ['e', 'f'], ['p', 'a'], ['d', 'g']]
len_l = len(l)
i = 0
while i < (len_l - 1):
for j in range(i + 1, len_l):
# i,j iterate over all pairs of l's elements including new
# elements from merged pairs. We use len_l because len(l)
# may change as we iterate
i_set = set(l[i])
j_set = set(l[j])
if len(i_set.intersection(j_set)) > 0:
# Remove these two from list
l.pop(j)
l.pop(i)
# Merge them and append to the orig. list
ij_union = list(i_set.union(j_set))
l.append(ij_union)
# len(l) has changed
len_l -= 1
# adjust 'i' because elements shifted
i -= 1
# abort inner loop, continue with next l[i]
break
i += 1
print l
# prints [['k'], ['a', 'c', 'b', 'e', 'd', 'g', 'f', 'o', 'p']]
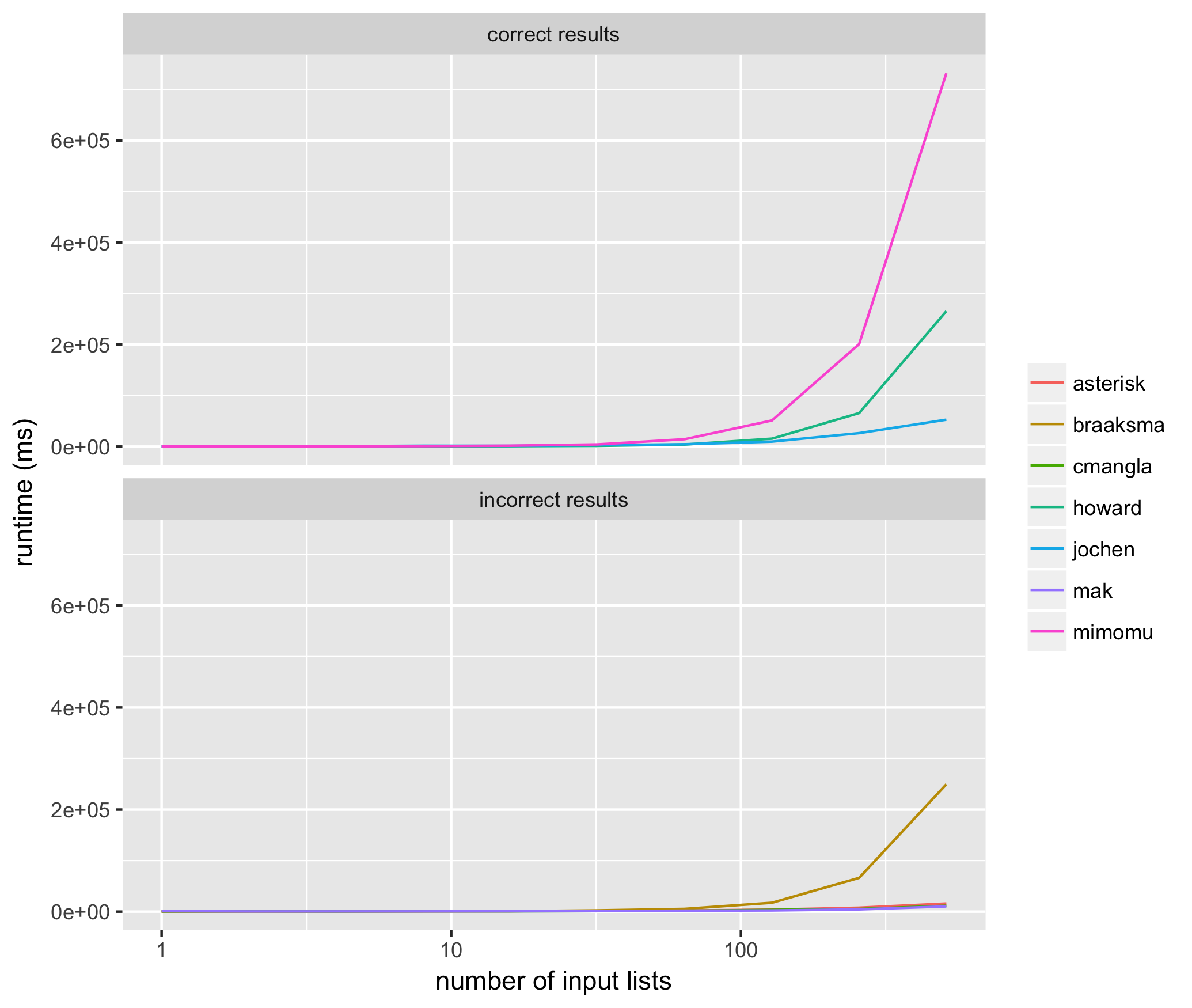
Simply speaking, you can use quick-find.
The key is to use two temporary list. The first is called elements, which stores all elements existing in all groups. The second is named labels. I got the inspiration from sklearn's kmeans algorithm. 'labels' stores the labels or the centroids of the elements. Here I simply let the first element in the cluster be the centroid. Initially, the values are from 0 to length-1, ascendingly.
For each group, I get their 'indices' in 'elements'. I then get the labels for group according to indices. And I calculate the min of the labels, that will be the new label for them. I replace all elements with labels in labels for group with the new label.
Or to say, for each iteration, I try to combine two or more existing groups. If the group has labels of 0 and 2 I find out the new label 0, that is the min of the two. I than replace them with 0.
def cluser_combine(groups):
n_groups=len(groups)
#first, we put all elements appeared in 'gruops' into 'elements'.
elements=list(set.union(*[set(g) for g in groups]))
#and sort elements.
elements.sort()
n_elements=len(elements)
#I create a list called clusters, this is the key of this algorithm.
#I was inspired by sklearn kmeans implementation.
#they have an attribute called labels_
#the url is here:
#https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
#i called this algorithm cluster combine, because of this inspiration.
labels=list(range(n_elements))
#for each group, I get their 'indices' in 'elements'
#I then get the labels for indices.
#and i calculate the min of the labels, that will be the new label for them.
#I replace all elements with labels in labels_for_group with the new label.
#or to say, for each iteration,
#i try to combine two or more existing groups.
#if the group has labels of 0 and 2
#i find out the new label 0, that is the min of the two.
#i than replace them with 0.
for i in range(n_groups):
#if there is only zero/one element in the group, skip
if len(groups[i])<=1:
continue
indices=list(map(elements.index, groups[i]))
labels_for_group=list(set([labels[i] for i in indices]))
#if their is only one label, all the elements in group are already have the same label, skip.
if len(labels_for_group)==1:
continue
labels_for_group.sort()
label=labels_for_group[0]
#combine
for k in range(n_elements):
if labels[k] in labels_for_group[1:]:
labels[k]=label
new_groups=[]
for label in set(labels):
new_group = [elements[i] for i, v in enumerate(labels) if v == label]
new_groups.append(new_group)
return new_groups
I printed out the detailed result for your question:
cluser_combine([['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g']])
elements:
['a', 'b', 'c', 'd', 'e', 'f', 'g', 'k', 'o', 'p']
labels:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
--------------------group 0-------------------------
the group is:
['a', 'b', 'c']
indices for the group in elements
[0, 1, 2]
labels before combination
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
combining...
labels after combination
[0, 0, 0, 3, 4, 5, 6, 7, 8, 9]
--------------------group 1-------------------------
the group is:
['b', 'd', 'e']
indices for the group in elements
[1, 3, 4]
labels before combination
[0, 0, 0, 3, 4, 5, 6, 7, 8, 9]
combining...
labels after combination
[0, 0, 0, 0, 0, 5, 6, 7, 8, 9]
--------------------group 2-------------------------
the group is:
['k']
--------------------group 3-------------------------
the group is:
['o', 'p']
indices for the group in elements
[8, 9]
labels before combination
[0, 0, 0, 0, 0, 5, 6, 7, 8, 9]
combining...
labels after combination
[0, 0, 0, 0, 0, 5, 6, 7, 8, 8]
--------------------group 4-------------------------
the group is:
['e', 'f']
indices for the group in elements
[4, 5]
labels before combination
[0, 0, 0, 0, 0, 5, 6, 7, 8, 8]
combining...
labels after combination
[0, 0, 0, 0, 0, 0, 6, 7, 8, 8]
--------------------group 5-------------------------
the group is:
['p', 'a']
indices for the group in elements
[9, 0]
labels before combination
[0, 0, 0, 0, 0, 0, 6, 7, 8, 8]
combining...
labels after combination
[0, 0, 0, 0, 0, 0, 6, 7, 0, 0]
--------------------group 6-------------------------
the group is:
['d', 'g']
indices for the group in elements
[3, 6]
labels before combination
[0, 0, 0, 0, 0, 0, 6, 7, 0, 0]
combining...
labels after combination
[0, 0, 0, 0, 0, 0, 0, 7, 0, 0]
([0, 0, 0, 0, 0, 0, 0, 7, 0, 0],
[['a', 'b', 'c', 'd', 'e', 'f', 'g', 'o', 'p'], ['k']])
Please refer to my github jupyter notebook for details
Here's my answer.
orig = [['a','b','c'],['b','d','e'],['k'],['o','p'],['e','f'],['p','a'],['d','g'], ['k'],['k'],['k']]
def merge_lists(orig):
def step(orig):
mid = []
mid.append(orig[0])
for i in range(len(mid)):
for j in range(1,len(orig)):
for k in orig[j]:
if k in mid[i]:
mid[i].extend(orig[j])
break
elif k == orig[j][-1] and orig[j] not in mid:
mid.append(orig[j])
mid = [sorted(list(set(x))) for x in mid]
return mid
result = step(orig)
while result != step(result):
result = step(result)
return result
merge_lists(orig)
[['a', 'b', 'c', 'd', 'e', 'f', 'g', 'o', 'p'], ['k']]
© 2022 - 2024 — McMap. All rights reserved.