Can a convolution function written in tail recursive form?

Question

I have a function that I want to write in tail recursive form. The function calculates the number of ways to get the sum of k by rolling an s sided die n times. I have seen the mathematical solution for this function on this answer. It is as follows:

My reference recursive implementation in R is:

sum_ways <- function(n_times, k_sum, s_side) {
  if (k_sum < n_times || k_sum > n_times * s_side) {
    return(0)
  } else if (n_times == 1) {
    return(1)
  } else {
    sigma_values <- sapply(
      1:s_side, 
      function(j) sum_ways(n_times - 1, k_sum - j, s_side)
    )
    return(sum(sigma_values))
  }
}

I have tried to re-write the function in continuation passing style as I have learned from this answer, but I wasn't successful. Is there a way to write this function in tail-recursive form?

EDIT

I know that R doesn't optimise for tail-recursion. My question is not R specific, a solution in any other language is just as welcome. Even if it is a language that does not optimise for tail-recursion.

Angelika

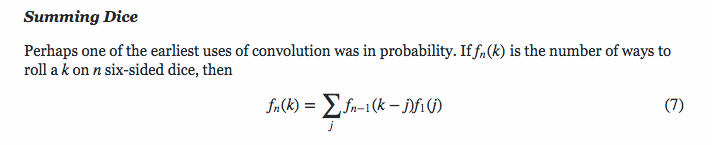
Look at ?Recall. – Incondite

@42- I'm glad to learn about this, thank you, but I couldn't see how it would help since I don't have the complication of changing the name of the function – Angelika

recursion will not be a very efficient implementation in this case, use dynamic programming / memoization to store the values of f already computed and reuse. – Blalock

@sandipan When I needed this function, I wrote my reference implementation and used it with memoization. It worked fine. I am not after an improved implementation at this point, I just want to know if tail-recursion is applicable in this case. – Angelika

Answer 1

sapply isn't in continuation-passing style, so you have to replace it.

Here's a translation to continuation-passing style in Python (another language that does not have proper tail calls):

def sum_ways_cps(n_times, k_sum, s_side, ctn):
    """Compute the number of ways to get the sum k by rolling an s-sided die
    n times. Then pass the answer to ctn."""

    if k_sum < n_times or k_sum > n_times * s_side:
        return ctn(0)
    elif n_times == 1:
        return ctn(1)
    else:
        f = lambda j, ctn: sum_ways_cps(n_times - 1, k_sum - j, s_side, ctn)
        return sum_cps(1, s_side + 1, 0, f, ctn)

def sum_cps(j, j_max, total_so_far, f, ctn):
    """Compute the sum of f(x) for x=j to j_max.
    Then pass the answer to ctn."""

    if j > j_max:
        return ctn(total_so_far)
    else:
        return f(j, lambda result: sum_cps(j + 1, j_max, total_so_far + result, f, ctn))


sum_ways_cps(2, 7, 6, print)  # 6

Winniewinnifred

Wow, I had a stackoverflow by reading it. Strictly speaking, would sum_ways_cps be considered tail recursive? – Angelika

The recursion here is that sum_ways_cps tail-calls sum_cps, which tail-calls f, which tail-calls sum_ways_cps. – Winniewinnifred

Can this be written as a single function? – Truncate

@ErenTantekin The main obstacle would be representing the state of the algorithm. The original algorithm contains non-tail recursive calls, and whenever one of those happens, the caller's local variables (representing "the work remaining to be done") are stored on the stack. The version in this answer uses a chain of continuations (lambdas) to represent the same information. If you want to avoid using lambdas, you'll have to represent the information some other way (using something like cons, perhaps). – Winniewinnifred

Answer 2

Try this (with recursion, we need to think of a linear recurrence relation if we want a tail recursive version):

f <- function(n, k) {
  if (n == 1) {                 # base case
    return(ifelse(k<=6, 1, 0))
  } else if (k > n*6 | k < n) { # some validation
    return(0)
  } 
  else {
    # recursive calls, f(1,j)=1, 1<=j<=6, otherwise 0  
    return(sum(sapply(1:min(k-n+1, 6), function(j) f(n-1,k-j))))  
  }
}

sapply(1:13, function(k) f(2, k))
# [1] 0 1 2 3 4 5 6 5 4 3 2 1 0

Blalock

This is almost the same with my implementation. I think it doesn't qualify as tail-recursive because the final action is not a call to itself but rather multiple calls to itself and than a summation. – Angelika

@Angelika since the original recurrence relation is in convolution form (that involves summation of multiple invocations of f), the exact recursive implementation will be also of the same type. If we can express the recurrence relation like f(n,k)=f(n-p,r)+g(r), for some integers p, r and some function g, then it can be written as a tail-recursive function. – Blalock

Doesn't that make the answer: "No it can't be done because..." rather than "Try this..."? – Angelika

@Angelika not sure, may be there is some nice recurrence formula that we don't know. we need to think. I just tried to come up with some solution which is recursive, somewhat close to your requirement. – Blalock