Calculate AUC in R?

Question

Given a vector of scores and a vector of actual class labels, how do you calculate a single-number AUC metric for a binary classifier in the R language or in simple English?

Page 9 of "AUC: a Better Measure..." seems to require knowing the class labels, and here is an example in MATLAB where I don't understand

R(Actual == 1))

Because R (not to be confused with the R language) is defined a vector but used as a function?

Baku

For anyone else who doesn't know, apparently AUC is the "Area Under the receiver operating characteristic Curve" – Syverson

Answer 1

As mentioned by others, you can compute the AUC using the ROCR package. With the ROCR package you can also plot the ROC curve, lift curve and other model selection measures.

You can compute the AUC directly without using any package by using the fact that the AUC is equal to the probability that a true positive is scored greater than a true negative.

For example, if pos.scores is a vector containing a score of the positive examples, and neg.scores is a vector containing the negative examples then the AUC is approximated by:

> mean(sample(pos.scores,1000,replace=T) > sample(neg.scores,1000,replace=T))
[1] 0.7261

will give an approximation of the AUC. You can also estimate the variance of the AUC by bootstrapping:

> aucs = replicate(1000,mean(sample(pos.scores,1000,replace=T) > sample(neg.scores,1000,replace=T)))

Macymad

For my test data set your replicated value is very similar to @jonw's (is 0.8504, yours 0.850591) except I don't need to install pROC. Thank you – Baku

@Baku @eric This is a terrible answer. You do NOT estimate the variance of the AUC - you only estimate the variance of the resampling process. To convince yourself, try changing the sample size in sample... divide it by 10, your variance is multiplied by 10. Multiply it by 10 and your variance is divided by 10. This is certainly not the desired behaviour to compute the variance of the AUC. – Hoarhound

In addition the answer should note that the estimate is as good as the number of replicates. Go to infinity and you get the actual AUC. – Hoarhound

Agree with @Calimo, that is not a bootstrap. To bootstrap you have to resample N data points with replacement M times, where N is the total size of the original data set and M can be whatever (usually a couple hundred or more). N is not arbitrary. If N is not set to the full data set size you'll get biased statistics. – Conversation

I'm a bit unclear on the base R method shown. Can it be calculated purely from the confusion matrix? In the context of a given confusion matrix, what would pos.scores and neg.scores be? – Herbivorous

Answer 2

With the package pROC you can use the function auc() like this example from the help page:

> data(aSAH)
> library(pROC) 
> # Syntax (response, predictor):
> auc(aSAH$outcome, aSAH$s100b)
Area under the curve: 0.7314

Terror

Answer 3

The ROCR package will calculate the AUC among other statistics:

auc.tmp <- performance(pred,"auc"); auc <- as.numeric([email protected])

Kym

I've used ROCR for plotting performance, but I don't see how it calculates a "single-number AUC metric" (from the original question). – Baku

auc.tmp <- performance(pred,"auc"); auc <- as.numeric([email protected]) – Dungdungan

Answer 4

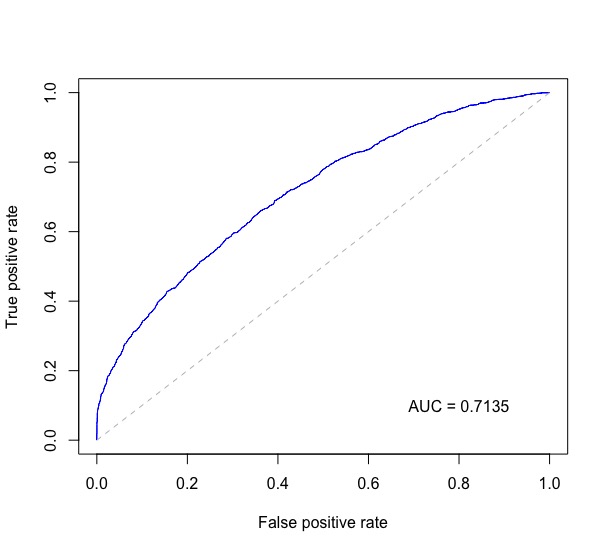
Without any additional packages:

true_Y = c(1,1,1,1,2,1,2,1,2,2)
probs = c(1,0.999,0.999,0.973,0.568,0.421,0.382,0.377,0.146,0.11)

getROC_AUC = function(probs, true_Y){
    probsSort = sort(probs, decreasing = TRUE, index.return = TRUE)
    val = unlist(probsSort$x)
    idx = unlist(probsSort$ix)  

    roc_y = true_Y[idx];
    stack_x = cumsum(roc_y == 2)/sum(roc_y == 2)
    stack_y = cumsum(roc_y == 1)/sum(roc_y == 1)    

    auc = sum((stack_x[2:length(roc_y)]-stack_x[1:length(roc_y)-1])*stack_y[2:length(roc_y)])
    return(list(stack_x=stack_x, stack_y=stack_y, auc=auc))
}

aList = getROC_AUC(probs, true_Y) 

stack_x = unlist(aList$stack_x)
stack_y = unlist(aList$stack_y)
auc = unlist(aList$auc)

plot(stack_x, stack_y, type = "l", col = "blue", xlab = "False Positive Rate", ylab = "True Positive Rate", main = "ROC")
axis(1, seq(0.0,1.0,0.1))
axis(2, seq(0.0,1.0,0.1))
abline(h=seq(0.0,1.0,0.1), v=seq(0.0,1.0,0.1), col="gray", lty=3)
legend(0.7, 0.3, sprintf("%3.3f",auc), lty=c(1,1), lwd=c(2.5,2.5), col="blue", title = "AUC")

Jowl

If you copy-paste this code and receive Error in plot.window(...) : need finite 'xlim' values, it's probably because your labels are 0-1, while @Jowl is using labels 1-2. – Shoemaker

It doesn't give the true AUC if two observations have the same probability and the order of the observation is not random. Otherwise nice and fast code. – Sanchez

Do not know why this solution does not work on my data, my probs are not normalized to be within [0,1] – Nash

Answer 5

I found some of the solutions here to be slow and/or confusing (and some of them don't handle ties correctly) so I wrote my own data.table based function auc_roc() in my R package mltools.

library(data.table)
library(mltools)

preds <- c(.1, .3, .3, .9)
actuals <- c(0, 0, 1, 1)

auc_roc(preds, actuals)  # 0.875

auc_roc(preds, actuals, returnDT=TRUE)
   Pred CountFalse CountTrue CumulativeFPR CumulativeTPR AdditionalArea CumulativeArea
1:  0.9          0         1           0.0           0.5          0.000          0.000
2:  0.3          1         1           0.5           1.0          0.375          0.375
3:  0.1          1         0           1.0           1.0          0.500          0.875

Thuja

This solution is much much faster than auc() method in pROC package! auc() method in pROC package is pretty slow if one has to calculate auc scores for multi-class or multiple output regression problem. – Nash

Answer 6

You can learn more about AUROC in this blog post by Miron Kursa:

https://mbq.me/blog/augh-roc/

He provides a fast function for AUROC:

# By Miron Kursa https://mbq.me
auroc <- function(score, bool) {
  n1 <- sum(!bool)
  n2 <- sum(bool)
  U  <- sum(rank(score)[!bool]) - n1 * (n1 + 1) / 2
  return(1 - U / n1 / n2)
}

Let's test it:

set.seed(42)
score <- rnorm(1e3)
bool  <- sample(c(TRUE, FALSE), 1e3, replace = TRUE)

pROC::auc(bool, score)
mltools::auc_roc(score, bool)
ROCR::performance(ROCR::prediction(score, bool), "auc")@y.values[[1]]
auroc(score, bool)

0.51371668847094
0.51371668847094
0.51371668847094
0.51371668847094

auroc() is 100 times faster than pROC::auc() and computeAUC().

auroc() is 10 times faster than mltools::auc_roc() and ROCR::performance().

print(microbenchmark(
  pROC::auc(bool, score),
  computeAUC(score[bool], score[!bool]),
  mltools::auc_roc(score, bool),
  ROCR::performance(ROCR::prediction(score, bool), "auc")@y.values,
  auroc(score, bool)
))

Unit: microseconds
                                                             expr       min
                                           pROC::auc(bool, score) 21000.146
                            computeAUC(score[bool], score[!bool]) 11878.605
                                    mltools::auc_roc(score, bool)  5750.651
 ROCR::performance(ROCR::prediction(score, bool), "auc")@y.values  2899.573
                                               auroc(score, bool)   236.531
         lq       mean     median        uq        max neval  cld
 22005.3350 23738.3447 22206.5730 22710.853  32628.347   100    d
 12323.0305 16173.0645 12378.5540 12624.981 233701.511   100   c 
  6186.0245  6495.5158  6325.3955  6573.993  14698.244   100  b  
  3019.6310  3300.1961  3068.0240  3237.534  11995.667   100 ab  
   245.4755   253.1109   251.8505   257.578    300.506   100 a   

Mauk

For larger sample sizes, bigstatsr::AUC() is even faster (implemented in C++). Disclaimer: I'm the author. – Entree

Answer 7

Combining code from ISL 9.6.3 ROC Curves, along with @J. Won.'s answer to this question and a few more places, the following plots the ROC curve and prints the AUC in the bottom right on the plot.

Below probs is a numeric vector of predicted probabilities for binary classification and test$label contains the true labels of the test data.

require(ROCR)
require(pROC)

rocplot <- function(pred, truth, ...) {
  predob = prediction(pred, truth)
  perf = performance(predob, "tpr", "fpr")
  plot(perf, ...)
  area <- auc(truth, pred)
  area <- format(round(area, 4), nsmall = 4)
  text(x=0.8, y=0.1, labels = paste("AUC =", area))

  # the reference x=y line
  segments(x0=0, y0=0, x1=1, y1=1, col="gray", lty=2)
}

rocplot(probs, test$label, col="blue")

This gives a plot like this:

Arda

Answer 8

I usually use the function ROC from the DiagnosisMed package. I like the graph it produces. AUC is returned along with it's confidence interval and it is also mentioned on the graph.

ROC(classLabels,scores,Full=TRUE)

Enface

As of July 20, 2016 this link cran.r-project.org/web/packages/DiagnosisMed/index.html says Package ‘DiagnosisMed’ was removed from the CRAN repository. – Arda

Answer 9

Along the lines of erik's response, you should also be able to calculate the ROC directly by comparing all possible pairs of values from pos.scores and neg.scores:

score.pairs <- merge(pos.scores, neg.scores)
names(score.pairs) <- c("pos.score", "neg.score")
sum(score.pairs$pos.score > score.pairs$neg.score) / nrow(score.pairs)

Certainly less efficient than the sample approach or the pROC::auc, but more stable than the former and requiring less installation than the latter.

Related: when I tried this it gave similar results to pROC's value, but not exactly the same (off by 0.02 or so); the result was closer to the sample approach with very high N. If anyone has ideas why that might be I'd be interested.

Ruche

One source of inaccuracy is dealing with ties. Technically you should take the probability that the positive case score is strictly greater than the negative score + 1/2 * prob they are equal. If all scores are unique this won't be a problem. – Mcgurn

Answer 10

Currently top voted answer is incorrect, because it disregards ties. When positive and negative scores are equal, then AUC should be 0.5. Below is corrected example.

computeAUC <- function(pos.scores, neg.scores, n_sample=100000) {
  # Args:
  #   pos.scores: scores of positive observations
  #   neg.scores: scores of negative observations
  #   n_samples : number of samples to approximate AUC

  pos.sample <- sample(pos.scores, n_sample, replace=T)
  neg.sample <- sample(neg.scores, n_sample, replace=T)
  mean(1.0*(pos.sample > neg.sample) + 0.5*(pos.sample==neg.sample))
}

Behlke

Answer 11

Calculating AUC with Metrics package is very easy and straightforward:

library(Metrics)

actual <- c(0, 0, 1, 1)
predicted <- c(.1, .3, .3, .9)

auc(actual, predicted)

0.875

Cursor