What are optimal scrypt work factors?

Question

I'm using a Java scrypt library for password storage. It calls for an N, r and p value when I encrypt things, which its documentation refers to as "CPU cost", "memory cost" and "parallelization cost" parameters. Only problem is, I don't actually know what they specifically mean, or what good values would be for them; perhaps they correspond somehow to the -t, -m and -M switches on Colin Percival's original app?

Does anyone have any suggestions for this? The library itself lists N = 16384, r = 8 and p = 1, but I don't know if this is strong or weak or what.

Knout

Tip only: if the password storage data might be hijacked (i.e. if there is backup), then store not the encryption of password, but of password concatenated with access key. This prevents dictionary attacks. – Murdock

I've posted a generic answer for the question, but I would welcome more detailed answers with some CPU timing and memory usage statistics of course. – Bithynia

@JoopEggen No idea what you want to say – Armitage

@CodeInChaos: if the data were stolen, and in the password field is stored encrypted the password and the access name (mixed), it is harder to hack, like to find common passwords like "secret" or "123456." As PASSWORD(), MD5(), and even normal SHA1() are not very safe, such extra technique should not be forgotten. – Murdock

@JoopEggen You're very vague. Do you mean using the username as salt? – Armitage

@Joop Eggen: No. SHA1 is not a Key derivation function, even with a salt. Do not use. SCrypt, on the other hand, is a very good one. Gladly enough, the OP is aware of the basic problem. – Jodijodie

@JoopEggen it is not stated in this post but scrypt +requires+ an explicit salt to be passed as a parameter (beside N/r/p). And, by the way, it is highly recommended to use a +random+ salt provided by a cryptographically secure PRNG (I often use 16 or 32 bytes salt) – Wahoo

Answer 1

As a start:

cpercival mentioned in his slides from 2009 something around

• (N = 2^14, r = 8, p = 1) for < 100ms (interactive use), and
• (N = 2^20, r = 8, p = 1) for < 5s (sensitive storage).

These values happen to be good enough for general use (password-db for some WebApp) even today (2012-09). Of course, specifics depend on the application.

Also, those values (mostly) mean:

• N: General work factor, iteration count.
• r: blocksize in use for underlying hash; fine-tunes the relative memory-cost.
• p: parallelization factor; fine-tunes the relative cpu-cost.

r and p are meant to accommodate for the potential issue that CPU speed and memory size and bandwidth do not increase as anticipated. Should CPU performance increase faster, you increase p, should instead a breakthrough in memory technology provide an order of magnitude improvement, you increase r. And N is there to keep up with the general doubling of performance per some timespan.

Important: All values change the result. (Updated:) This is the reason why all scrypt parameters are stored in the result string.

Jodijodie

Btw, the scrypt parameters are automatically stored in the resulting key, so they don't need to be stored separately. This means you can have different values for the parameters in user passwords in the password storage as time passes and when users change their password, the key (=hashed password) is generated with the current parameter values. – Foreignism

Thanks for pointing this out; I didn't realize that the linked Java implementation does this in a sane way. – Jodijodie

@Jodijodie You should update your answer. Not all people read all the comments :) – Noncommittal

"Btw, the scrypt parameters are automatically stored in the resulting key, so they don't need to be stored separately. " - just to clarify (for other readers) this only applies to the Java implementation. The scrypt standard and other implementations don't require the cost/parameters to be stored with the resulting hash. – Dinh

The Scrypt.Net implementation does the same thing, the author states its a port of the C implementation. – Demesne

Just to clarify @elithrar's comment, the format used by Colin Percival himself (the author of scrypt) stores the work factors in the resulting key (as detailed at security.stackexchange.com/questions/88678#answer-91050) – Rillings

@chrisV That mentions the node scrypt module. Does the scrypt spec/paper itself specify the storage format? – Dinh

@Dinh the scrypt paper doesn't set out the format in detail (it is suggested in Definition 4, p11), but it can be seen in the code or more usefully in Colin's format spec (sorry for the late response). – Rillings

Answer 2

Short answer

So that it takes 250 ms to verify a password

Long answer

The memory required for scrypt to operate is calculated as:

128 bytes × cost (N) × blockSizeFactor (r)

for the parameters you quote (N=16384, r=8, p=1)

128×16384×8 = 16,777,216 bytes = 16 MB

You have to take this into account when choosing parameters.

Bcrypt is "weaker" than Scrypt (although still three orders of magnitude stronger than PBKDF2) because it only requires 4 KB of memory. You want to make it difficult to parallelize cracking in hardware. For example, if a video card has 1.5 GB of on-board memory and you tuned scrypt to consume 1 GB of memory:

128×16384×512 = 1,073,741,824 bytes = 1 GB

then an attacker could not parallelize it on their video card. But then your application/phone/server would need to use 1 GB of RAM every time they calculated a password.

It helps me to think about the scrypt parameters as a rectangle. Where:

• the width is the amount of memory required (128*N*r)
• the height is the number of iterations performed
• and the resulting area is the overall hardness

• the cost (N) increases both memory usage and iterations.
• the blockSizeFactor (r) increases memory usage.

The remaining parameter parallelization (p) means that you have to do the entire thing 2, 3, or more times:

If you had more memory than CPU, you could calculate the three separate paths in parallel - requiring triple the memory:

But in all real-world implementations, it is calculated in series, tripling the calculations needed:

In reality, nobody has ever chosen a p factor other than p=1.

What are the ideal factors?

• As much RAM as you can spare
• for as much time as you can spare!

Bonus Chart

Graphical version of above; you're targeting ~250ms:

Notes:

• the vertical axis is log scale
• Cost factor (horizontal) itself is log (iterations = 2^CostFactor)
• Highlighted in the r=8 curve

And zoomed in version of above to the reasonable area, again looking at the ~250ms magnitude:

Bonus Chatter

• scrypt is weaker than bcrypt for password storage if scrypt is configured to use less than 4 MB ¹
• Argon2 (i/d/id) is weaker than bcrypt when it comes to password hashing for authentication (i.e. <1,000 ms verification time) ²

Gladdie

Thank you for this analysis, It's really useful. Only one issue: I'm currently testing this on Android using Bouncy Castle implementation - bouncycastle.org/docs/docs1.5on/org/bouncycastle/crypto/… and the memory usage is exactly 2x higher (128× N× r× 2). Any idea why ...? – Dissatisfy

@Tron I'm going to guess because there's a point where it copies the memory to another buffer (i.e. passing the 16MB to PBKDF2, which performs the actual final key derivation). – Gladdie

Improvement needed: While it is true that N is the only factor impacting the number of pseudo-random jumps around the large block of memory, the computation cost is still determined by both N and r because there are 4*r Salsa20/8 iterations for each of the N iterations (2*r to generate the memory block, then 2*r while jumping around the memory block). – Visitation

may I ask why r=1 doesnt extend beyond 2^14? – Marindamarinduque

but this answer is really nice and explains scrypt very well, great stuff. – Marindamarinduque

@Marindamarinduque That's a good question. The scrypt algorithm has a requirement that N < 2^(128*r/8). When r=1, that simplifies to N < 2^16. I'd have to dig deeper, but it's something with the way the internal BlockMix function uses ROMix. – Gladdie

okay thats's intresting I thought that it might have been forgotten or similar, but is there a reason why every r>10 stops at 2^19? or do the simply shoot off the scale afterwards? – Marindamarinduque

@Marindamarinduque Eventually my 32-bit process either a) runs out of free space in it's 2 GB address space, or b) it wants to allocate more memory than can fit in the signed 32-bit parameter to GetMem takes. – Gladdie

well at least 2^20 and r16 is exactly 2048 so no wonder that one doesnt work. – Marindamarinduque

If you could explain, there's something I still don't get. What's the problem with needing 16 MB per calculation, or 1 GB out of 1.5 GB? That's cleaned after each calculation, no? If it is, it's just take 1 GB again infinitely. If it's not cleaned, then I didn't get something and will have to read more about this. – Kazbek

@DADi590 You might run into RAM problems on your web-server if you have 8 people trying to login at once, each consuming1 GB of RAM. – Gladdie

Ah no, I mean for the attacker attempting to brute-force the password or whatever (though, I was not thinking at that point of view, so still thank you). What does the higher memory requirements do? Doesn't seem to be nothing special 16 MB with the default parameters. Unless that adds up for some reason (I would think it would be allocated > thrown away > allocated > ....) – Kazbek

The more memory required during computation means there is less parallel attacks you can mount of a GPU. If a GPU comes with 4 GB of RAM, then that means you can theoretically create an OpenCL shader that can perform 4096÷16=256 parallel computations at a time. Increasing the memory requirement (e.g. to 3 GB) means you could only run one parallel attack on a GPU. The more memory the more resistant to parallelization on special hardware. – Gladdie

Answer 3

I don't want to step on the excellent answers provided above, but no one really talks about why "r" has the value it has. The low-level answer provided by the Colin Percival's Scrypt paper is that it relates to the "memory latency-bandwidth product". But what does that actually mean?

If you're doing Scrypt right, you should have a large memory block which is mostly sitting in main memory. Main memory takes time to pull from. When an iteration of the block-jumping loop first selects an element from the large block to mix into the working buffer, it has to wait on the order of 100 ns for the first chunk of data to arrive. Then it has to request another, and wait for it to arrive.

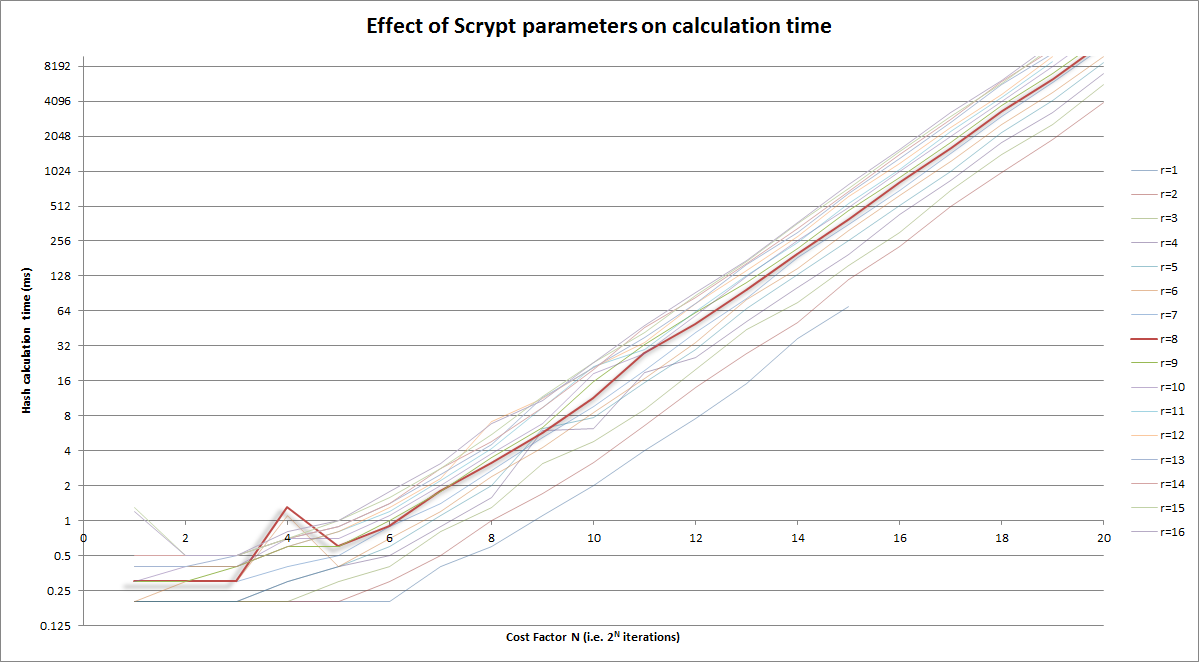
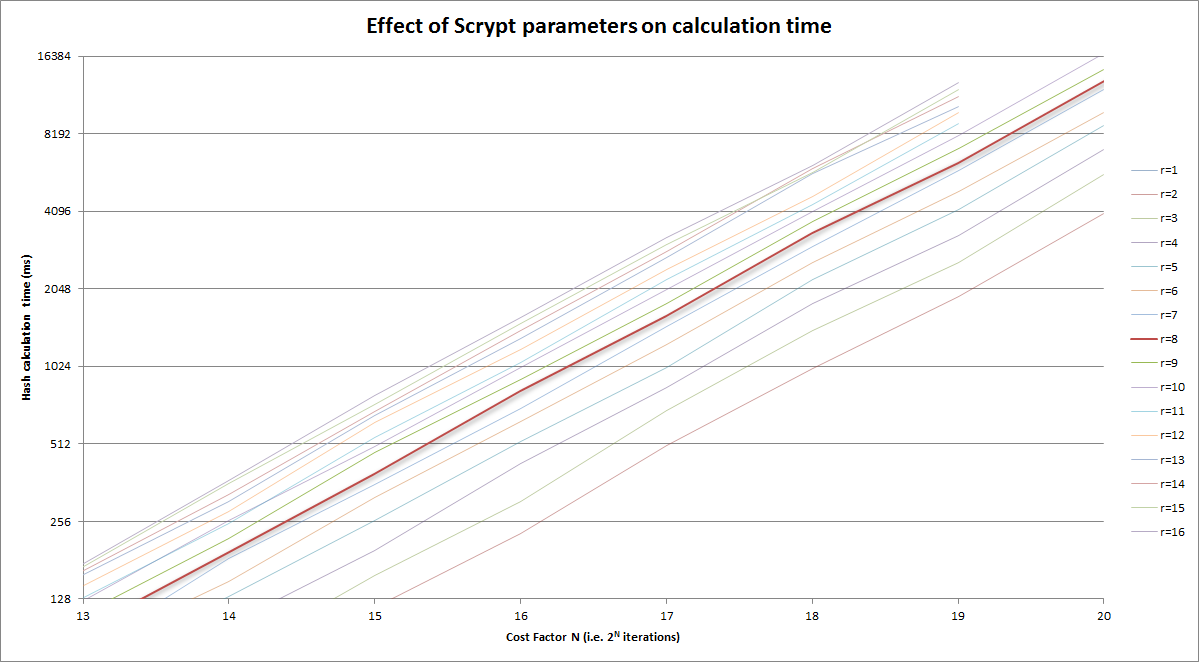
For r = 1, you'd be doing 4nr Salsa20/8 iterations and 2n latency-imbued reads from main memory.

This isn't good, because it means that an attacker could get an advantage over you by building a system with reduced latency to main memory.

But if you increase r and proportionally decrease N, you are able to achieve the same memory requirements and do the same number of computations as before--except that you've traded some random accesses for sequential accesses. Extending sequential access allows either the CPU or the library to prefetch the next required blocks of data efficiently. While the initial latency is still there, the reduced or eliminated latency for the later blocks averages the initial latency out to a minimal level. Thus, an attacker would gain little from improving their memory technology over yours.

However, there is a point of diminishing returns with increasing r, and that is related to the "memory latency-bandwidth product" referred to before. What this product indicates is how many bytes of data can be in transit from main memory to the processor at any given time. It's the same idea as a highway--if it takes 10 minutes to travel from point A to point B (latency), and the road delivers 10 cars/minute to point B from point A (bandwidth), the roadway between points A and B contains 100 cars. So, the optimal r relates to how many 64-byte chunks of data you can request at once, in order to cover up the latency of that initial request.

This improves the speed of the algorithm, allowing you to either increase N for more memory and computations or to increase p for more computations, as desired.

There are some other issues with increasing "r" too much, which I haven't seen discussed much:

1. Increasing r while decreasing N reduces the number of pseudorandom jumps around memory. Sequential accesses are easier to optimize, and could give an attacker a window. As Colin Percival noted to me on Twitter, larger r could allow an attacker to use a lower cost, slower storage technology, reducing their costs considerably (https://twitter.com/cperciva/status/661373931870228480).
2. The size of the working buffer is 1024r bits, so the number of possible end products, which will eventually be fed into PBKDF2 to produce the Scrypt output key, is 2^1024r. The number of permutations (possible sequences) of jumps around the large memory block is 2^NlogN. Which means that there are 2^NlogN possible products of the memory-jumping loop. If 1024r > NlogN, that would seem to indicate that the working buffer is being under-mixed. While I don't know this for sure, and would love to see a proof or disproof, it may be possible for correlations to be found between the working buffer's result and the sequence of jumps, which could allow an attacker an opportunity to reduce their memory requirements without as-greatly increased computational cost. Again, this is an observation based on the numbers--it may be that everything is so well-mixed in every round that this isn't a problem. r = 8 is well below this potential threshold for the standard N = 2^14 -- for N = 2^14, this threshold would be r = 224.

To sum up all the recommendations:

1. Choose r to be just large enough to average out the effects of memory latency on your device and no more. Keep in mind that the value Colin Percival recommended, r = 8, appears to remain fairly optimal broadly for memory technology, and this apparently hasn't changed much in 8 years; 16 may be ever so slightly better.
2. Decide on how big a chunk of memory you want to use per thread, keeping in mind this affects computation time as well, and set N accordingly.
3. Increase p arbitrarily high to what your usage can tolerate (note: on my system and using my own implementation, p = 250 (4 threads) with N = 16384 and r = 8 takes ~5 seconds), and enable threading if you can deal with the added memory cost.
4. When tuning, prefer large N and memory block size to increased p and computation time. Scrypt's primary benefit comes from its large memory block size.

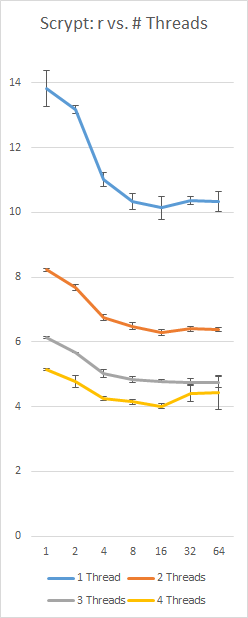
A benchmark of my own implementation of Scrypt on a Surface Pro 3 with an i5-4300 (2 cores, 4 threads), using a constant 128Nr = 16 MB and p = 230; left-axis is seconds, bottom axis is r value, error bars are +/- 1 standard deviation:

Visitation

Great table! Looks like with 1 thread, N=8192, r=16, p=1 (16MB memory used), the time cost would be about 40ms per auth attempt on your system and implementation. That's a really nice cost. N=16834, r=8, p=1 is only very slightly slower, but it does look like there's a slight-but-consistent advantage to the larger r. – Ugly