In short:
I have implemented a simple (multi-key) hash table with buckets (containing several elements) that exactly fit a cacheline. Inserting into a cacheline bucket is very simple, and the critical part of the main loop.
I have implemented three versions that produce the same outcome and should behave the same.
The mystery
However, I'm seeing wild performance differences by a surprisingly large factor 3, despite all versions having the exact same cacheline access pattern and resulting in identical hash table data.
The best implementation insert_ok suffers around a factor 3 slow down compared to insert_bad & insert_alt on my CPU (i7-7700HQ).
One variant insert_bad is a simple modification of insert_ok that adds an extra unnecessary linear search within the cacheline to find the position to write to (which it already knows) and does not suffer this x3 slow down.
The exact same executable shows insert_ok a factor 1.6 faster compared to insert_bad & insert_alt on other CPUs (AMD 5950X (Zen 3), Intel i7-11800H (Tiger Lake)).
# see https://github.com/cr-marcstevens/hashtable_mystery
$ ./test.sh
model name : Intel(R) Core(TM) i7-7700HQ CPU @ 2.80GHz
==============================
CXX=g++ CXXFLAGS=-std=c++11 -O2 -march=native -falign-functions=64
tablesize: 117440512 elements: 67108864 loadfactor=0.571429
- test insert_ok : 11200ms
- test insert_bad: 3164ms
(outcome identical to insert_ok: true)
- test insert_alt: 3366ms
(outcome identical to insert_ok: true)
tablesize: 117440813 elements: 67108864 loadfactor=0.571427
- test insert_ok : 10840ms
- test insert_bad: 3301ms
(outcome identical to insert_ok: true)
- test insert_alt: 3579ms
(outcome identical to insert_ok: true)
The Code
// insert element in hash_table
inline void insert_ok(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; ++c)
{
bucket_t& B = table_ok[b];
// if bucket non-full then store element and return
if (B.size != bucket_size)
{
B.keys[B.size] = k;
B.values[B.size] = 1;
++B.size;
++table_count;
return;
}
// increase b w/ wrap around
if (++b == table_size)
b = 0;
}
}
// equivalent to insert_ok
// but uses a stupid linear search to store the element at the target position
inline void insert_bad(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; ++c)
{
bucket_t& B = table_bad[b];
// if bucket non-full then store element and return
if (B.size != bucket_size)
{
for (size_t i = 0; i < bucket_size; ++i)
{
if (i == B.size)
{
B.keys[i] = k;
B.values[i] = 1;
++B.size;
++table_count;
return;
}
}
}
// increase b w/ wrap around
if (++b == table_size)
b = 0;
}
}
// instead of using bucket_t.size, empty elements are marked by special empty_key value
// a bucket is filled first to last, so bucket is full if last element key != empty_key
uint64_t empty_key = ~uint64_t(0);
inline void insert_alt(uint64_t k)
{
// compute target bucket
uint64_t b = mod(k);
// bounded linear search for first non-full bucket
for (size_t c = 0; c < 1024; ++c)
{
bucket_t& B = table_alt[b];
// if bucket non-full then store element and return
if (B.keys[bucket_size-1] == empty_key)
{
for (size_t i = 0; i < bucket_size; ++i)
{
if (B.keys[i] == empty_key)
{
B.keys[i] = k;
B.values[i] = 1;
++table_count;
return;
}
}
}
// increase b w/ wrap around
if (++b == table_size)
b = 0;
}
}
My analysis
I've tried various modifications to the loop C++, but inherently it's so simple, the compiler will produce the same assembly. It's really not obvious from the resulting assembly what the factor 3 loss might cause. I've tried measuring with perf, but I can't seem to pinpoint any meaningful difference.
Comparing the assembly of the 3 versions which are all just relatively small loops, there is nothing that suggests anything close that may cause a factor 3 loss between these versions.
Hence, I presume the 3x slow down is a weird effect of automatic prefetching, or branch prediction, or instruction/jump alignment or maybe a combination of those.
Does anybody have better insights or ways to measure what effects might actually be at play here?
Details
I've created a small working C++11 example that demonstrates the problem. The code is available at https://github.com/cr-marcstevens/hashtable_mystery
This also includes my own static binaries that demonstrate this problem on my CPU, as different compilers may produce different code. As well as dumped assembly code for all three hash table versions.
perf event measurements
Here are a lot of perf event measurements. I've focused on ones that include the word miss and stall.
Each event has two lines:
- the first line corresponds to
insert_okwhich has the slowdown - the second line corresponds to
insert_altwhich has an additional loop and additional work, but ends up faster
=== L1-dcache-load-misses ===
insert_ok : 171411476
insert_alt: 244244027
=== L1-dcache-loads ===
insert_ok : 775468123
insert_alt: 1038574743
=== L1-dcache-stores ===
insert_ok : 621353009
insert_alt: 554244145
=== L1-icache-load-misses ===
insert_ok : 69666
insert_alt: 259102
=== LLC-load-misses ===
insert_ok : 70519701
insert_alt: 71399242
=== LLC-loads ===
insert_ok : 130909270
insert_alt: 134776189
=== LLC-store-misses ===
insert_ok : 16782747
insert_alt: 16851787
=== LLC-stores ===
insert_ok : 17072141
insert_alt: 17534866
=== arith.divider_active ===
insert_ok : 26810
insert_alt: 26611
=== baclears.any ===
insert_ok : 2038060
insert_alt: 7648128
=== br_inst_retired.all_branches ===
insert_ok : 546479449
insert_alt: 938434022
=== br_inst_retired.all_branches_pebs ===
insert_ok : 546480454
insert_alt: 938412921
=== br_inst_retired.cond_ntaken ===
insert_ok : 237470651
insert_alt: 433439086
=== br_inst_retired.conditional ===
insert_ok : 477604946
insert_alt: 802468807
=== br_inst_retired.far_branch ===
insert_ok : 1058138
insert_alt: 1052510
=== br_inst_retired.near_call ===
insert_ok : 227076
insert_alt: 227074
=== br_inst_retired.near_return ===
insert_ok : 227072
insert_alt: 227070
=== br_inst_retired.near_taken ===
insert_ok : 307946256
insert_alt: 503926433
=== br_inst_retired.not_taken ===
insert_ok : 237458763
insert_alt: 433429466
=== br_misp_retired.all_branches ===
insert_ok : 36443541
insert_alt: 90626754
=== br_misp_retired.all_branches_pebs ===
insert_ok : 36441027
insert_alt: 90622375
=== br_misp_retired.conditional ===
insert_ok : 36454196
insert_alt: 90591031
=== br_misp_retired.near_call ===
insert_ok : 173
insert_alt: 169
=== br_misp_retired.near_taken ===
insert_ok : 19032467
insert_alt: 40361420
=== branch-instructions ===
insert_ok : 546476228
insert_alt: 938447476
=== branch-load-misses ===
insert_ok : 36441314
insert_alt: 90611299
=== branch-loads ===
insert_ok : 546472151
insert_alt: 938435143
=== branch-misses ===
insert_ok : 36436325
insert_alt: 90597372
=== bus-cycles ===
insert_ok : 222283508
insert_alt: 88243938
=== cache-misses ===
insert_ok : 257067753
insert_alt: 475091979
=== cache-references ===
insert_ok : 445465943
insert_alt: 590770464
=== cpu-clock ===
insert_ok : 10333.94 msec cpu-clock:u # 1.000 CPUs utilized
insert_alt: 4766.53 msec cpu-clock:u # 1.000 CPUs utilized
=== cpu-cycles ===
insert_ok : 25273361574
insert_alt: 11675804743
=== cpu_clk_thread_unhalted.one_thread_active ===
insert_ok : 223196489
insert_alt: 88616919
=== cpu_clk_thread_unhalted.ref_xclk ===
insert_ok : 222719013
insert_alt: 88467292
=== cpu_clk_unhalted.one_thread_active ===
insert_ok : 223380608
insert_alt: 88212476
=== cpu_clk_unhalted.ref_tsc ===
insert_ok : 32663820508
insert_alt: 12901195392
=== cpu_clk_unhalted.ref_xclk ===
insert_ok : 221957996
insert_alt: 88390991
insert_alt: === cpu_clk_unhalted.ring0_trans ===
insert_ok : 374
insert_alt: 373
=== cpu_clk_unhalted.thread ===
insert_ok : 25286801620
insert_alt: 11714137483
=== cycle_activity.cycles_l1d_miss ===
insert_ok : 16278956219
insert_alt: 7417877493
=== cycle_activity.cycles_l2_miss ===
insert_ok : 15607833569
insert_alt: 7054717199
=== cycle_activity.cycles_l3_miss ===
insert_ok : 12987627072
insert_alt: 6745771672
=== cycle_activity.cycles_mem_any ===
insert_ok : 23440206343
insert_alt: 9027220495
=== cycle_activity.stalls_l1d_miss ===
insert_ok : 16194872307
insert_alt: 4718344050
=== cycle_activity.stalls_l2_miss ===
insert_ok : 15350067722
insert_alt: 4578933898
=== cycle_activity.stalls_l3_miss ===
insert_ok : 12697354271
insert_alt: 4457980047
=== cycle_activity.stalls_mem_any ===
insert_ok : 20930005455
insert_alt: 4555461595
=== cycle_activity.stalls_total ===
insert_ok : 22243173394
insert_alt: 6561416461
=== dTLB-load-misses ===
insert_ok : 67817362
insert_alt: 63603879
=== dTLB-loads ===
insert_ok : 775467642
insert_alt: 1038562488
=== dTLB-store-misses ===
insert_ok : 8823481
insert_alt: 13050341
=== dTLB-stores ===
insert_ok : 621353007
insert_alt: 554244145
=== dsb2mite_switches.count ===
insert_ok : 93894397
insert_alt: 315793354
=== dsb2mite_switches.penalty_cycles ===
insert_ok : 9216240937
insert_alt: 206393788
=== dtlb_load_misses.miss_causes_a_walk ===
insert_ok : 177266866
insert_alt: 101439773
=== dtlb_load_misses.stlb_hit ===
insert_ok : 2994329
insert_alt: 35601646
=== dtlb_load_misses.walk_active ===
insert_ok : 4747616986
insert_alt: 3893609232
=== dtlb_load_misses.walk_completed ===
insert_ok : 67817832
insert_alt: 63591832
=== dtlb_load_misses.walk_completed_4k ===
insert_ok : 67817841
insert_alt: 63596148
=== dtlb_load_misses.walk_pending ===
insert_ok : 6495600072
insert_alt: 5987182579
=== dtlb_store_misses.miss_causes_a_walk ===
insert_ok : 89895924
insert_alt: 21841494
=== dtlb_store_misses.stlb_hit ===
insert_ok : 4940907
insert_alt: 21970231
=== dtlb_store_misses.walk_active ===
insert_ok : 1784142210
insert_alt: 903334856
=== dtlb_store_misses.walk_completed ===
insert_ok : 8845884
insert_alt: 13071262
=== dtlb_store_misses.walk_completed_4k ===
insert_ok : 8822993
insert_alt: 12936414
=== dtlb_store_misses.walk_pending ===
insert_ok : 1842905733
insert_alt: 933039119
=== exe_activity.1_ports_util ===
insert_ok : 991400575
insert_alt: 1433908710
=== exe_activity.2_ports_util ===
insert_ok : 782270731
insert_alt: 1314443071
=== exe_activity.3_ports_util ===
insert_ok : 556847358
insert_alt: 1158115803
=== exe_activity.4_ports_util ===
insert_ok : 427323800
insert_alt: 783571280
=== exe_activity.bound_on_stores ===
insert_ok : 299732094
insert_alt: 303475333
=== exe_activity.exe_bound_0_ports ===
insert_ok : 227569792
insert_alt: 348959512
=== frontend_retired.dsb_miss ===
insert_ok : 6771584
insert_alt: 93700643
=== frontend_retired.itlb_miss ===
insert_ok : 1115
insert_alt: 1689
=== frontend_retired.l1i_miss ===
insert_ok : 3639
insert_alt: 3857
=== frontend_retired.l2_miss ===
insert_ok : 2826
insert_alt: 2830
=== frontend_retired.latency_ge_1 ===
insert_ok : 9206268
insert_alt: 178345368
=== frontend_retired.latency_ge_128 ===
insert_ok : 2708
insert_alt: 2703
=== frontend_retired.latency_ge_16 ===
insert_ok : 403492
insert_alt: 820950
=== frontend_retired.latency_ge_2 ===
insert_ok : 4981263
insert_alt: 85781924
=== frontend_retired.latency_ge_256 ===
insert_ok : 802
insert_alt: 970
=== frontend_retired.latency_ge_2_bubbles_ge_1 ===
insert_ok : 56936702
insert_alt: 225712704
=== frontend_retired.latency_ge_2_bubbles_ge_2 ===
insert_ok : 10312026
insert_alt: 163227996
=== frontend_retired.latency_ge_2_bubbles_ge_3 ===
insert_ok : 7599252
insert_alt: 122841752
=== frontend_retired.latency_ge_32 ===
insert_ok : 3599
insert_alt: 3317
=== frontend_retired.latency_ge_4 ===
insert_ok : 2627373
insert_alt: 42287077
=== frontend_retired.latency_ge_512 ===
insert_ok : 418
insert_alt: 241
=== frontend_retired.latency_ge_64 ===
insert_ok : 2474
insert_alt: 2802
=== frontend_retired.latency_ge_8 ===
insert_ok : 528748
insert_alt: 951836
=== frontend_retired.stlb_miss ===
insert_ok : 769
insert_alt: 562
=== hw_interrupts.received ===
insert_ok : 9330
insert_alt: 3738
=== iTLB-load-misses ===
insert_ok : 456094
insert_alt: 90739
=== iTLB-loads ===
insert_ok : 949
insert_alt: 1031
=== icache_16b.ifdata_stall ===
insert_ok : 1145821
insert_alt: 862403
=== icache_64b.iftag_hit ===
insert_ok : 1378406022
insert_alt: 4459469241
=== icache_64b.iftag_miss ===
insert_ok : 61812
insert_alt: 57204
=== icache_64b.iftag_stall ===
insert_ok : 56551468
insert_alt: 82354039
=== idq.all_dsb_cycles_4_uops ===
insert_ok : 896374829
insert_alt: 1610100578
=== idq.all_dsb_cycles_any_uops ===
insert_ok : 1217878089
insert_alt: 2739912727
=== idq.all_mite_cycles_4_uops ===
insert_ok : 315979501
insert_alt: 480165021
=== idq.all_mite_cycles_any_uops ===
insert_ok : 1053703958
insert_alt: 2251382760
=== idq.dsb_cycles ===
insert_ok : 1218891711
insert_alt: 2744099964
=== idq.dsb_uops ===
insert_ok : 5828442701
insert_alt: 10445095004
=== idq.mite_cycles ===
insert_ok : 470409312
insert_alt: 1664892371
=== idq.mite_uops ===
insert_ok : 1407396065
insert_alt: 4515396737
=== idq.ms_cycles ===
insert_ok : 583601361
insert_alt: 587996351
=== idq.ms_dsb_cycles ===
insert_ok : 218346
insert_alt: 74155
=== idq.ms_mite_uops ===
insert_ok : 1266443204
insert_alt: 1277980465
=== idq.ms_switches ===
insert_ok : 149106449
insert_alt: 150392336
=== idq.ms_uops ===
insert_ok : 1266950097
insert_alt: 1277330690
=== idq_uops_not_delivered.core ===
insert_ok : 1871959581
insert_alt: 6531069387
=== idq_uops_not_delivered.cycles_0_uops_deliv.core ===
insert_ok : 289301660
insert_alt: 946930713
=== idq_uops_not_delivered.cycles_fe_was_ok ===
insert_ok : 24668869613
insert_alt: 9335642949
=== idq_uops_not_delivered.cycles_le_1_uop_deliv.core ===
insert_ok : 393750384
insert_alt: 1344106460
=== idq_uops_not_delivered.cycles_le_2_uop_deliv.core ===
insert_ok : 506090534
insert_alt: 1824690188
=== idq_uops_not_delivered.cycles_le_3_uop_deliv.core ===
insert_ok : 688462029
insert_alt: 2416339045
=== ild_stall.lcp ===
insert_ok : 380
insert_alt: 480
=== inst_retired.any ===
insert_ok : 4760842560
insert_alt: 5470438932
=== inst_retired.any_p ===
insert_ok : 4760919037
insert_alt: 5470404264
=== inst_retired.prec_dist ===
insert_ok : 4760801654
insert_alt: 5470649220
=== inst_retired.total_cycles_ps ===
insert_ok : 25175372339
insert_alt: 11718929626
=== instructions ===
insert_ok : 4760805219
insert_alt: 5470497783
=== int_misc.clear_resteer_cycles ===
insert_ok : 199623562
insert_alt: 671083279
=== int_misc.recovery_cycles ===
insert_ok : 314434729
insert_alt: 704406698
=== itlb.itlb_flush ===
insert_ok : 303
insert_alt: 248
=== itlb_misses.miss_causes_a_walk ===
insert_ok : 19537
insert_alt: 116729
=== itlb_misses.stlb_hit ===
insert_ok : 11323
insert_alt: 5557
=== itlb_misses.walk_active ===
insert_ok : 2809766
insert_alt: 4070194
=== itlb_misses.walk_completed ===
insert_ok : 24298
insert_alt: 45251
=== itlb_misses.walk_completed_4k ===
insert_ok : 34084
insert_alt: 29759
=== itlb_misses.walk_pending ===
insert_ok : 853764
insert_alt: 2817933
=== l1d.replacement ===
insert_ok : 171135334
insert_alt: 244967326
=== l1d_pend_miss.fb_full ===
insert_ok : 354631656
insert_alt: 382309583
=== l1d_pend_miss.pending ===
insert_ok : 16792436441
insert_alt: 22979721104
=== l1d_pend_miss.pending_cycles ===
insert_ok : 16377420892
insert_alt: 7349245429
=== l1d_pend_miss.pending_cycles_any ===
insert_ok : insert_alt: === l2_lines_in.all ===
insert_ok : 303009088
insert_alt: 411750486
=== l2_lines_out.non_silent ===
insert_ok : 157208112
insert_alt: 309484666
=== l2_lines_out.silent ===
insert_ok : 127379047
insert_alt: 84169481
=== l2_lines_out.useless_hwpf ===
insert_ok : 70374658
insert_alt: 144359127
=== l2_lines_out.useless_pref ===
insert_ok : 70747103
insert_alt: 142931540
=== l2_rqsts.all_code_rd ===
insert_ok : 71254
insert_alt: 242327
=== l2_rqsts.all_demand_data_rd ===
insert_ok : 137366274
insert_alt: 143507049
=== l2_rqsts.all_demand_miss ===
insert_ok : 150071420
insert_alt: 150820168
=== l2_rqsts.all_demand_references ===
insert_ok : 154854022
insert_alt: 160487082
=== l2_rqsts.all_pf ===
insert_ok : 170261458
insert_alt: 282476184
=== l2_rqsts.all_rfo ===
insert_ok : 17575896
insert_alt: 16938897
=== l2_rqsts.code_rd_hit ===
insert_ok : 79800
insert_alt: 381566
=== l2_rqsts.code_rd_miss ===
insert_ok : 25800
insert_alt: 33755
=== l2_rqsts.demand_data_rd_hit ===
insert_ok : 5191029
insert_alt: 9831101
=== l2_rqsts.demand_data_rd_miss ===
insert_ok : 132253891
insert_alt: 133965310
=== l2_rqsts.miss ===
insert_ok : 305347974
insert_alt: 414758839
=== l2_rqsts.pf_hit ===
insert_ok : 14639778
insert_alt: 19484420
=== l2_rqsts.pf_miss ===
insert_ok : 156092998
insert_alt: 263293430
=== l2_rqsts.references ===
insert_ok : 326549998
insert_alt: 443460029
=== l2_rqsts.rfo_hit ===
insert_ok : 11650
insert_alt: 21474
=== l2_rqsts.rfo_miss ===
insert_ok : 17544467
insert_alt: 16835137
=== l2_trans.l2_wb ===
insert_ok : 157044674
insert_alt: 308107712
=== ld_blocks.no_sr ===
insert_ok : 14
insert_alt: 13
=== ld_blocks.store_forward ===
insert_ok : 158
insert_alt: 128
=== ld_blocks_partial.address_alias ===
insert_ok : 5155853
insert_alt: 17867414
=== load_hit_pre.sw_pf ===
insert_ok : 10840795
insert_alt: 11072297
=== longest_lat_cache.miss ===
insert_ok : 257061118
insert_alt: 471152073
=== longest_lat_cache.reference ===
insert_ok : 445701577
insert_alt: 583870610
=== machine_clears.count ===
insert_ok : 3926377
insert_alt: 4280080
=== machine_clears.memory_ordering ===
insert_ok : 97177
insert_alt: 25407
=== machine_clears.smc ===
insert_ok : 138579
insert_alt: 305423
=== mem-stores ===
insert_ok : 621353009
insert_alt: 554244143
=== mem_inst_retired.all_loads ===
insert_ok : 775473590
insert_alt: 1038559807
=== mem_inst_retired.all_stores ===
insert_ok : 621353013
insert_alt: 554244145
=== mem_inst_retired.lock_loads ===
insert_ok : 85
insert_alt: 85
=== mem_inst_retired.split_loads ===
insert_ok : 171
insert_alt: 174
=== mem_inst_retired.split_stores ===
insert_ok : 53
insert_alt: 49
=== mem_inst_retired.stlb_miss_loads ===
insert_ok : 68308539
insert_alt: 18088047
=== mem_inst_retired.stlb_miss_stores ===
insert_ok : 264054
insert_alt: 819551
=== mem_load_l3_hit_retired.xsnp_none ===
insert_ok : 231116
insert_alt: 175217
=== mem_load_retired.fb_hit ===
insert_ok : 6510722
insert_alt: 95952490
=== mem_load_retired.l1_hit ===
insert_ok : 698271530
insert_alt: 920982402
=== mem_load_retired.l1_miss ===
insert_ok : 69525335
insert_alt: 20089897
=== mem_load_retired.l2_hit ===
insert_ok : 1451905
insert_alt: 773356
=== mem_load_retired.l2_miss ===
insert_ok : 68085186
insert_alt: 19474303
=== mem_load_retired.l3_hit ===
insert_ok : 222829
insert_alt: 155958
=== mem_load_retired.l3_miss ===
insert_ok : 67879593
insert_alt: 19244746
=== memory_disambiguation.history_reset ===
insert_ok : 97621
insert_alt: 25831
=== minor-faults ===
insert_ok : 1048716
insert_alt: 1048718
=== node-loads ===
insert_ok : 71473780
insert_alt: 71377840
=== node-stores ===
insert_ok : 16781161
insert_alt: 16842666
=== offcore_requests.all_data_rd ===
insert_ok : 284186682
insert_alt: 392110677
=== offcore_requests.all_requests ===
insert_ok : 530876505
insert_alt: 777784382
=== offcore_requests.demand_code_rd ===
insert_ok : 34252
insert_alt: 45896
=== offcore_requests.demand_data_rd ===
insert_ok : 133468710
insert_alt: 134288893
=== offcore_requests.demand_rfo ===
insert_ok : 17612516
insert_alt: 17062276
=== offcore_requests.l3_miss_demand_data_rd ===
insert_ok : 71616594
insert_alt: 82917520
=== offcore_requests_buffer.sq_full ===
insert_ok : 2001445
insert_alt: 3113287
=== offcore_requests_outstanding.all_data_rd ===
insert_ok : 35577129549
insert_alt: 78698308135
=== offcore_requests_outstanding.cycles_with_data_rd ===
insert_ok : 17518017620
insert_alt: 7940272202
=== offcore_requests_outstanding.demand_code_rd ===
insert_ok : 11085819
insert_alt: 9390881
=== offcore_requests_outstanding.demand_data_rd ===
insert_ok : 15902243707
insert_alt: 21097348926
=== offcore_requests_outstanding.demand_data_rd_ge_6 ===
insert_ok : 1225437
insert_alt: 317436422
=== offcore_requests_outstanding.demand_rfo ===
insert_ok : 1074492442
insert_alt: 1157902315
=== offcore_response.demand_code_rd.any_response ===
insert_ok : 53675
insert_alt: 69683
=== offcore_response.demand_code_rd.l3_hit.any_snoop ===
insert_ok : 19407
insert_alt: 29704
=== offcore_response.demand_code_rd.l3_hit.snoop_none ===
insert_ok : 12675
insert_alt: 11951
=== offcore_response.demand_code_rd.l3_miss.any_snoop ===
insert_ok : 34617
insert_alt: 40868
=== offcore_response.demand_code_rd.l3_miss.spl_hit ===
insert_ok : 0
insert_alt: 753
=== offcore_response.demand_data_rd.any_response ===
insert_ok : 131014821
insert_alt: 134813171
=== offcore_response.demand_data_rd.l3_hit.any_snoop ===
insert_ok : 59713328
insert_alt: 50254543
=== offcore_response.demand_data_rd.l3_miss.any_snoop ===
insert_ok : 71431585
insert_alt: 83916030
=== offcore_response.demand_data_rd.l3_miss.spl_hit ===
insert_ok : 244837
insert_alt: 6441992
=== offcore_response.demand_rfo.any_response ===
insert_ok : 16876557
insert_alt: 17619450
=== offcore_response.demand_rfo.l3_hit.any_snoop ===
insert_ok : 907432
insert_alt: 45127
=== offcore_response.demand_rfo.l3_hit.snoop_none ===
insert_ok : 787567
insert_alt: 794579
=== offcore_response.demand_rfo.l3_hit_e.any_snoop ===
insert_ok : 496938
insert_alt: 173658
=== offcore_response.demand_rfo.l3_hit_e.snoop_none ===
insert_ok : 779919
insert_alt: 50575
=== offcore_response.demand_rfo.l3_hit_m.any_snoop ===
insert_ok : 128627
insert_alt: 25483
=== offcore_response.demand_rfo.l3_miss.any_snoop ===
insert_ok : 16782186
insert_alt: 16847970
=== offcore_response.demand_rfo.l3_miss.snoop_none ===
insert_ok : 16782647
insert_alt: 16850104
=== offcore_response.demand_rfo.l3_miss.spl_hit ===
insert_ok : 0
insert_alt: 1364
=== offcore_response.other.any_response ===
insert_ok : 137231000
insert_alt: 189526494
=== offcore_response.other.l3_hit.any_snoop ===
insert_ok : 62695084
insert_alt: 51005882
=== offcore_response.other.l3_hit.snoop_none ===
insert_ok : 62975018
insert_alt: 50217349
=== offcore_response.other.l3_hit_e.any_snoop ===
insert_ok : 62770215
insert_alt: 50691817
=== offcore_response.other.l3_hit_e.snoop_none ===
insert_ok : 62602591
insert_alt: 50642954
=== offcore_response.other.l3_miss.any_snoop ===
insert_ok : 74247236
insert_alt: 139212975
=== offcore_response.other.l3_miss.snoop_none ===
insert_ok : 75911794
insert_alt: 141076520
=== other_assists.any ===
insert_ok : 1
insert_alt: 3
=== page-faults ===
insert_ok : 1048719
insert_alt: 1048718
=== partial_rat_stalls.scoreboard ===
insert_ok : 530950991
insert_alt: 539869553
=== ref-cycles ===
insert_ok : 32546980212
insert_alt: 12930921138
=== resource_stalls.any ===
insert_ok : 21923576648
insert_alt: 5205690082
=== resource_stalls.sb ===
insert_ok : 397908667
insert_alt: 402738367
=== rs_events.empty_cycles ===
insert_ok : 1173721723
insert_alt: 1880165720
=== rs_events.empty_end ===
insert_ok : 87752182
insert_alt: 160792701
=== sw_prefetch_access.t0 ===
insert_ok : 20835202
insert_alt: 20599176
=== task-clock ===
insert_ok : 10416.86 msec task-clock:u # 1.000 CPUs utilized
insert_alt: 4767.78 msec task-clock:u # 1.000 CPUs utilized
=== tlb_flush.stlb_any ===
insert_ok : 1835393
insert_alt: 1835396
=== topdown-fetch-bubbles ===
insert_ok : 1904143421
insert_alt: 6543146396
=== topdown-slots-issued ===
insert_ok : 7538371393
insert_alt: 14449966516
=== topdown-slots-retired ===
insert_ok : 5267325162
insert_alt: 5849706597
=== uops_dispatched_port.port_0 ===
insert_ok : 1252121297
insert_alt: 1489605354
=== uops_dispatched_port.port_1 ===
insert_ok : 1379316967
insert_alt: 1585037107
=== uops_dispatched_port.port_2 ===
insert_ok : 1140861153
insert_alt: 1785053149
=== uops_dispatched_port.port_3 ===
insert_ok : 1187151423
insert_alt: 1828975838
=== uops_dispatched_port.port_4 ===
insert_ok : 1577171758
insert_alt: 1557761857
=== uops_dispatched_port.port_5 ===
insert_ok : 1341370655
insert_alt: 1653599117
=== uops_dispatched_port.port_6 ===
insert_ok : 1856735970
insert_alt: 4387464794
=== uops_dispatched_port.port_7 ===
insert_ok : 508351498
insert_alt: 603583315
=== uops_executed.core ===
insert_ok : 7225522677
insert_alt: 12716368190
=== uops_executed.core_cycles_ge_1 ===
insert_ok : 3041586797
insert_alt: 5168421550
=== uops_executed.core_cycles_ge_2 ===
insert_ok : 2017794537
insert_alt: 3653591208
=== uops_executed.core_cycles_ge_3 ===
insert_ok : 1225785335
insert_alt: 2316014066
=== uops_executed.core_cycles_ge_4 ===
insert_ok : 657121809
insert_alt: 1143390519
=== uops_executed.core_cycles_none ===
insert_ok : 22191507320
insert_alt: 6563722081
=== uops_executed.cycles_ge_1_uop_exec ===
insert_ok : 3040999757
insert_alt: 5175668459
=== uops_executed.cycles_ge_2_uops_exec ===
insert_ok : 2015520940
insert_alt: 3659989196
=== uops_executed.cycles_ge_3_uops_exec ===
insert_ok : 1224025952
insert_alt: 2319025110
=== uops_executed.cycles_ge_4_uops_exec ===
insert_ok : 657094113
insert_alt: 1141381027
=== uops_executed.stall_cycles ===
insert_ok : 22350754164
insert_alt: 6590978048
=== uops_executed.thread ===
insert_ok : 7214521925
insert_alt: 12697219901
=== uops_executed.x87 ===
insert_ok : 2992
insert_alt: 3337
=== uops_issued.any ===
insert_ok : 7531354736
insert_alt: 14462113169
=== uops_issued.slow_lea ===
insert_ok : 2136241
insert_alt: 2115308
=== uops_issued.stall_cycles ===
insert_ok : 23244177475
insert_alt: 7416801878
=== uops_retired.macro_fused ===
insert_ok : 410461916
insert_alt: 735050350
=== uops_retired.retire_slots ===
insert_ok : 5265023980
insert_alt: 5855259326
=== uops_retired.stall_cycles ===
insert_ok : 23513958928
insert_alt: 9630258867
=== uops_retired.total_cycles ===
insert_ok : 25266688635
insert_alt: 11703285605
Background
I'm implementing a cryptanalytic attack in C++11 and need to find many collisions between two large lists (both generated on the fly). A crucial part of the attack thus just consists of two critical loops:
- first populating a hash table with one list
- then matching the other list against the hash table.
The hash table operations are thus performance critical, and a factor 3 slow down means the attack is 3x slower.
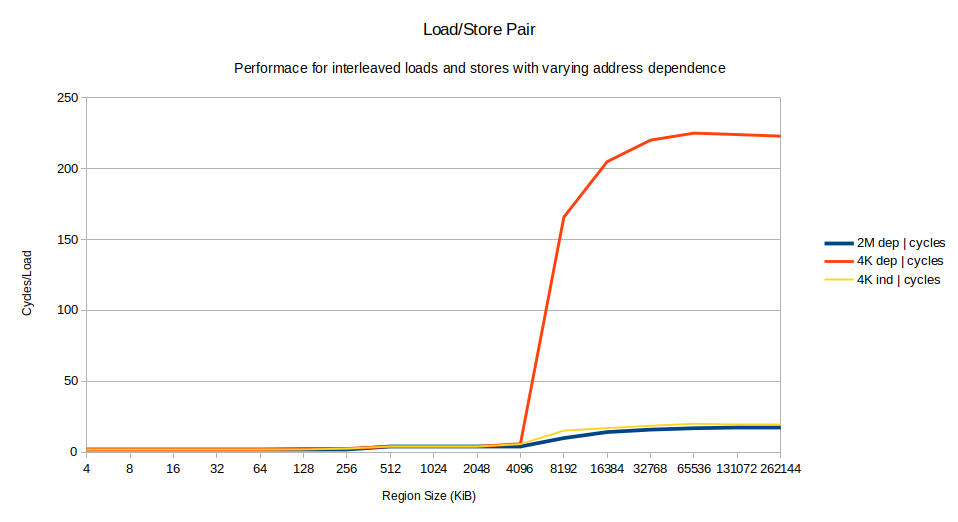
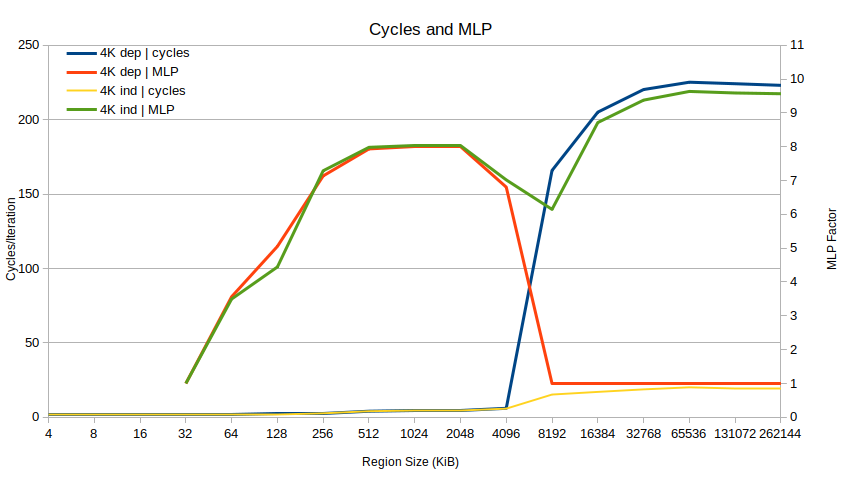
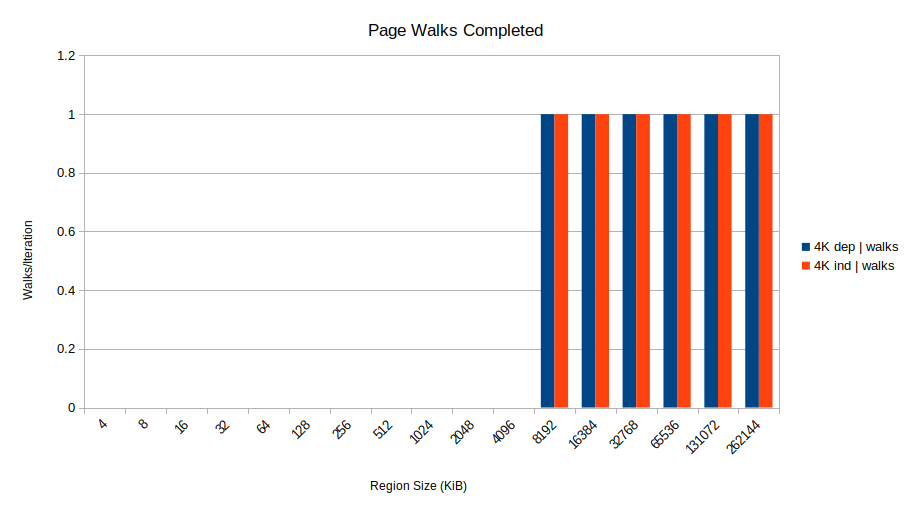
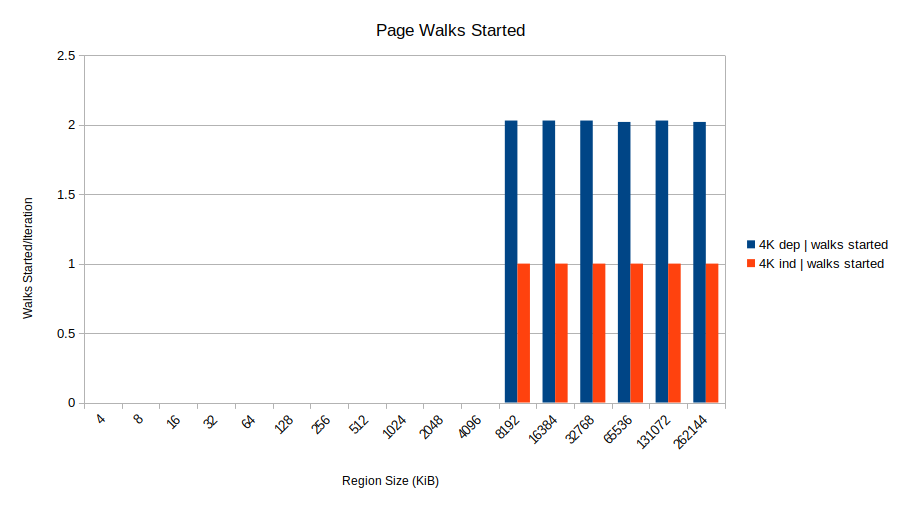
Regarding design: Besides trying to minimize memory usage, I'm also trying to have a typical hash table operation operate on just a single cacheline. As I expect that will increase overall attack performance, especially when running the attack on all CPU cores.

b.sizeis spilling. 2)b.sizeis regularly 0 or 1 and highly predictable so the versions that loop oniare essentially "skipping" the memory dependency on the index. Also, which performance counters change values between the versions? I would at the very least check if its FE related withlsd.uops,idq_dsb.uops, andidq_mite.uops. You also may check the port distribution of uops and branch misses. – Awestrickeninsert_okhas a "slow" and "fast" mode. The only perf counter I can see that really seems to be predictive of the results ismachine_clears_memory_ordering. Opposite of expectation with high clear counter we get "fast" mode and with low clear count we get "slow" mode. Its possible that the low machine clears indicate the slowdown is from entering a serialized state due to memory disambiguation. – Awestrickensize_t sz = 0; if(sz != B.size) { sz = B.size; }....and useszto index it is exclusively the fastest version. This does point that the perf issue is related to some serialization / dependency between the load ofB.sizeand the store address calculation. – Awestrickenport78(store ports on tigerlake). @PeterCordes will also know better but is it possible that the the store dependent on the load "preemptively" executes expected L1 hit on load and we are getting replays? Not sure how else to explain it. – Awestrickeninsert_okwas about as fast as the others and 1/5 "slow mode" where it was an order of magnitude slower. – Awestrickeninsert_okis run first in all your tests. To eliminate phenomena like cache heating, CPU throttling, etc, do you get the same result if you run your three functions in a different order? – Ceressize_t sz = 0; if (sz != B.size) { sz = B.size; }and usingszas index. That didn't speed things up unless I removed the++B.size;. However when removing that line then you'll always get the trivial case that B.size == 0, and it won't be correct anymore. – Carbonariinsert_okruns 1.6x faster thaninsert_badon their Tiger Lake CPU. So presumably it's with different binaries on those machines, at least due to-march=native, and maybe different kernels or libraries aligning data differently in memory? – Strokeinsert_okversion is that it's the only one where this is a non-speculative dependency between the load ofB.sizeand the store address location. – Awestrickenhash_table_*wrapper functions to 256 bytes to remove FE noise. I can "reproduce" with 256 byte alignment. I cannot reproduce with 64 byte alignment. I think this further points to the memory disambiguation unit as that is the only way I can see this alignment affecting MLP. Note with 64/256 alignment I don't see any difference in FE related counters. – Awestricken