Epsilon(ε) productions and LR(0) grammars and LL(1) grammars

Question

At many places (for example in this answer here), I have seen it is written that an LR(0) grammar cannot contain ε productions.

Also in Wikipedia I have seen statements like: An ε free LL(1) grammar is also SLR(1).

---

Now the problem which I am facing is that I cannot reason out the logic behind these statements.

Well, I know that LR(0) grammars accept the languages accepted by a DPDA by empty stack, i.e. the language they accept must have prefix property. [This prefix property can, however, be dealt with if we assume end markers and as such given any language the prefix property shall always be satisfied. Many texts like Theory of Computation by Sipser assume this end marker to simply their argument]. That being said, we can say (informally?) that a grammar is LR(0) if there is no state in the canonical collection of LR(0) items that have a shift-reduce conflict or reduce-reduce conflict.

With this background, I tried to consider the following grammar:

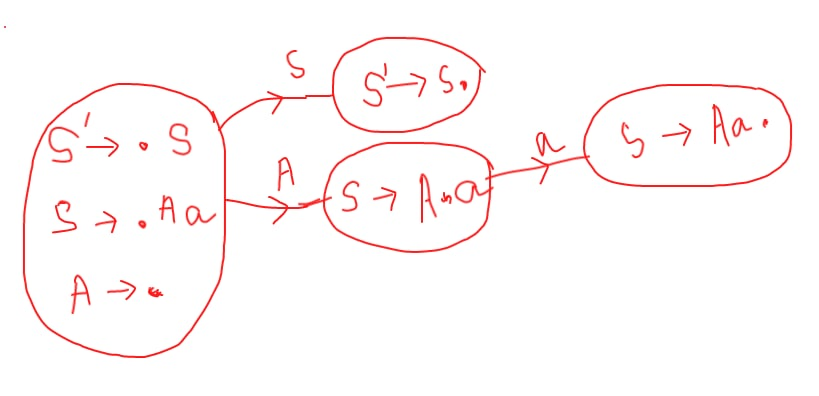
S -> Aa
A -> ε

canonical collection of LR(0) items

In the above DFA, I find that there is no state which has a shift-reduce conflict or reduce-reduce conflict.

So this grammar should be LR(0) as per my analysis. But it also has ε production.

Isn't this example contradicting the statement:

"no grammar with ε productions can be LR(0)"

I guess if I know the logic behind the above quoted statement then I can understand the concept better.

---

Actually my main problem arose with the statement :

An ε free LL(1) grammar is also SLR(1).

When I asked one of my friends, he gave the argument that as the LL(1) grammar is ε free hence it is LR(0) and hence it is SLR(1).

But I could not understand his logic either. When I asked him about reasoning, he started sharing post regarding "grammar with ε productions can never be LR(0)"...

But personally I could not think of any logic as to how "ε free LL(1) grammar is SLR(1)". Is it really related to the above property of "grammar with ε productions cannot be LR(0)"? If so, please do help me out.. If not, then should I consider asking a separate question for the second confusion?

---

I have got my concepts of compiler design from the dragon book by Ullman only. Also the knowledge of TOC from Ullman and from few other texts like Sipser, Linz.

Pajamas

Your start state has a shift-reduce conflict. – Avail

@MattTimmermans why do you say so? personally I feel there is no SR conflict based on the concept in Ullman text. The reduce is due to A->.. But there is no shift move. As for the A, I would say that it is goto and not shift...[I say this as per conventions in Ullman text] – Pajamas

After the first A is reduced, you are back in the start state and can reduce A again or shift to A.a. – Avail

@matt: after A is reduced, the next state is GOTO(S_0, A), which is not S_0. There is no reduction possible in that state. – Weksler

Abhishek: for the future: why do you insist on asking questions like this on SO? It is not a programming question and it is irritating to not have MathJax available to format math. SO's argument for not enabling MathJax is that programming questions don't usually benefit from math formatting; whether or not one agrees with that assessment (I don't, as it happens), this is not a counterexample since it involves no programming. Asking it on Computer Science would be more appropriate and a courtesy for prospective answerers who care about the appearance of their posts. – Weksler

And heres an answer from Computer Science which covers the same ground. – Weksler

@Weksler the link actually points to the root site... and not any answer... please can you check it once... – Pajamas

@Weksler should I delete this question here and repost it in cs.stackexchange? then you could answer the same there... Sorry as I used a reference from SO I thought that it would be appropriate probably to ask here. [I was wrong :(] sorry for that... once long ago I had asked a question on some stack exchange site... some one shifted the question to a more appropriate site... of StackExchange... is something like that possible here? – Pajamas

@AbhishekGhosh: no, leave it be. I answered here. But next time, please use Computer Science. The Q could be migrated by a mod but they've got enough to do. The "link" in my other comment is actually two consecutive links; if you look closely you'll see they're separated by a non-linked space. The first one points at the answer. – Weksler

@Weksler ok. I shall follow from next time... And sorry... Since the links are quite close, I actually did not notice the minute white-space between the two blue underlines.. yes got the answer... – Pajamas

Answer 1

A notable feature of your grammar is that A could just be eliminated. It serves absolutely no purpose. (By "eliminated", I mean simply removing all references to it; leaving productions otherwise intact.)

It is true that it's existence doesn't preclude the grammar from being LR(0). Similarly, a grammar with an unreachable non-terminal and an ε-production for that non-terminal could also be LR(0).

So it would be more accurate to say that a grammar cannot be LR(0) if it has a productive non-terminal with both an ε-production and some other productive production. But since we usually only consider reduced grammars without pointless non-terminals, I'm not sure that this additional pedantry serves much purpose.

---

As for your question about ε-free LL(1) grammars, here's a rough outline:

If an ε-free grammar is not LR(0), then there is some state with both a shift and a reduce action. Since the grammar is ε-free, that state was reached by way of a shift or a goto. The previous state must then have had two different productions with the same FIRST set, contradicting the LL(1) condition.

Weksler

if it has a productive non-terminal has both an ε-production and some other productive production. I cannot get the meaning of this sentence... Might there is some sort of typo... because firstly the sentence reads weird... please can you have a look... – Pajamas

Sorry. I fixed it. "Productive" means that every non-terminal in the production can derive a sequence consisting only of terminals (or more accurately, without non-terminals). – Weksler

got the point... I knew the concept ("productive") it seems... but knew it with a different name... "generating". – Pajamas