First of all, I assume that you call features the variables and not the samples/observations. In this case, you could do something like the following by creating a biplot function that shows everything in one plot. In this example, I am using the iris data.
Before the example, please note that the basic idea when using PCA as a tool for feature selection is to select variables according to the magnitude (from largest to smallest in absolute values) of their coefficients (loadings). See my last paragraph after the plot for more details.
Overview:
PART1: I explain how to check the importance of the features and how to plot a biplot.
PART2: I explain how to check the importance of the features and how to save them into a pandas dataframe using the feature names.
PART 1:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
import pandas as pd
from sklearn.preprocessing import StandardScaler
iris = datasets.load_iris()
X = iris.data
y = iris.target
#In general a good idea is to scale the data
scaler = StandardScaler()
scaler.fit(X)
X=scaler.transform(X)
pca = PCA()
x_new = pca.fit_transform(X)
def myplot(score,coeff,labels=None):
xs = score[:,0]
ys = score[:,1]
n = coeff.shape[0]
scalex = 1.0/(xs.max() - xs.min())
scaley = 1.0/(ys.max() - ys.min())
plt.scatter(xs * scalex,ys * scaley, c = y)
for i in range(n):
plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
if labels is None:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'g', ha = 'center', va = 'center')
else:
plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.xlabel("PC{}".format(1))
plt.ylabel("PC{}".format(2))
plt.grid()
#Call the function. Use only the 2 PCs.
myplot(x_new[:,0:2],np.transpose(pca.components_[0:2, :]))
plt.show()
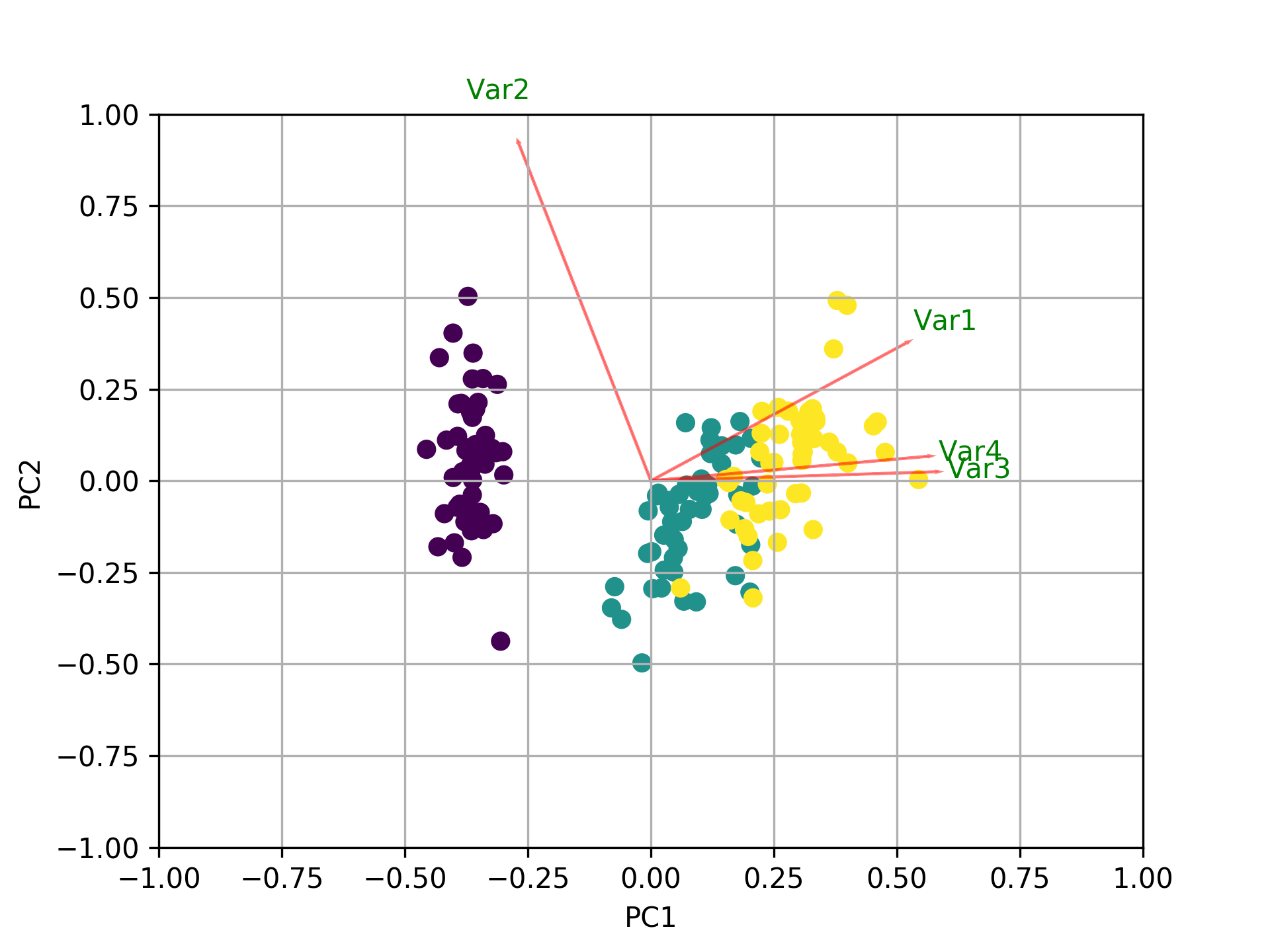
Visualize what's going on using the biplot
![enter image description here]()
Now, the importance of each feature is reflected by the magnitude of the corresponding values in the eigenvectors (higher magnitude - higher importance)
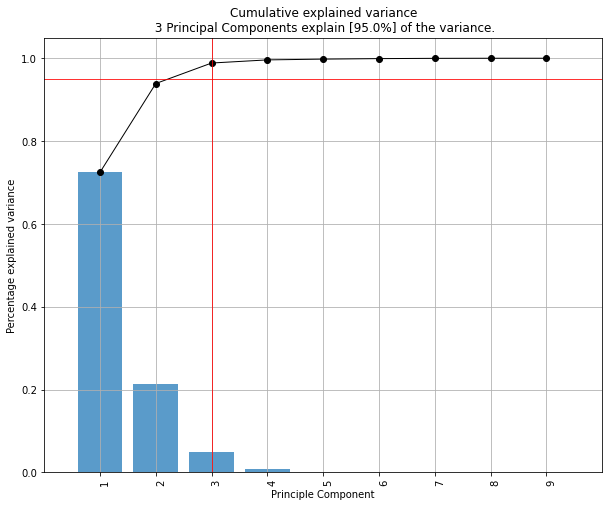
Let's see first what amount of variance does each PC explain.
pca.explained_variance_ratio_
[0.72770452, 0.23030523, 0.03683832, 0.00515193]
PC1 explains 72% and PC2 23%. Together, if we keep PC1 and PC2 only, they explain 95%.
Now, let's find the most important features.
print(abs( pca.components_ ))
[[0.52237162 0.26335492 0.58125401 0.56561105]
[0.37231836 0.92555649 0.02109478 0.06541577]
[0.72101681 0.24203288 0.14089226 0.6338014 ]
[0.26199559 0.12413481 0.80115427 0.52354627]]
Here, pca.components_ has shape [n_components, n_features]. Thus, by looking at the PC1 (First Principal Component) which is the first row: [0.52237162 0.26335492 0.58125401 0.56561105]] we can conclude that feature 1, 3 and 4 (or Var 1, 3 and 4 in the biplot) are the most important. This is also clearly visible from the biplot (that's why we often use this plot to summarize the information in a visual way).
To sum up, look at the absolute values of the Eigenvectors' components corresponding to the k largest Eigenvalues. In sklearn the components are sorted by explained_variance_. The larger they are these absolute values, the more a specific feature contributes to that principal component.
PART 2:
The important features are the ones that influence more the components and thus, have a large absolute value/score on the component.
To get the most important features on the PCs with names and save them into a pandas dataframe use this:
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np
np.random.seed(0)
# 10 samples with 5 features
train_features = np.random.rand(10,5)
model = PCA(n_components=2).fit(train_features)
X_pc = model.transform(train_features)
# number of components
n_pcs= model.components_.shape[0]
# get the index of the most important feature on EACH component
# LIST COMPREHENSION HERE
most_important = [np.abs(model.components_[i]).argmax() for i in range(n_pcs)]
initial_feature_names = ['a','b','c','d','e']
# get the names
most_important_names = [initial_feature_names[most_important[i]] for i in range(n_pcs)]
# LIST COMPREHENSION HERE AGAIN
dic = {'PC{}'.format(i): most_important_names[i] for i in range(n_pcs)}
# build the dataframe
df = pd.DataFrame(dic.items())
This prints:
0 1
0 PC0 e
1 PC1 d
So on the PC1 the feature named e is the most important and on PC2 the d.
Nice article as well here: https://towardsdatascience.com/pca-clearly-explained-how-when-why-to-use-it-and-feature-importance-a-guide-in-python-7c274582c37e?source=friends_link&sk=65bf5440e444c24aff192fedf9f8b64f