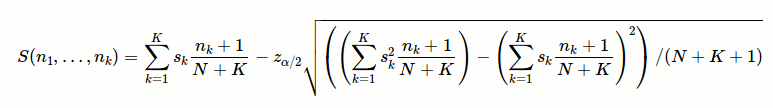Evan Miller shows a Bayesian approach to ranking 5-star ratings:
![enter image description here]()
where
nk is the number of k-star ratings, sk is the "worth" (in points) of k stars, N is the total number of votesK is the maximum number of stars (e.g. K=5, in a 5-star rating system)z_alpha/2 is the 1 - alpha/2 quantile of a normal distribution. If you want 95% confidence (based on the Bayesian posterior distribution) that the actual sort criterion is at least as big as the computed sort criterion, choose z_alpha/2 = 1.65.
In Python, the sorting criterion can be calculated with
def starsort(ns):
"""
http://www.evanmiller.org/ranking-items-with-star-ratings.html
"""
N = sum(ns)
K = len(ns)
s = list(range(K,0,-1))
s2 = [sk**2 for sk in s]
z = 1.65
def f(s, ns):
N = sum(ns)
K = len(ns)
return sum(sk*(nk+1) for sk, nk in zip(s,ns)) / (N+K)
fsns = f(s, ns)
return fsns - z*math.sqrt((f(s2, ns)- fsns**2)/(N+K+1))
For example, if an item has 60 five-stars, 80 four-stars, 75 three-stars, 20 two-stars and 25 one-stars, then its overall star rating would be about 3.4:
x = (60, 80, 75, 20, 25)
starsort(x)
# 3.3686975120774694
and you can sort a list of 5-star ratings with
sorted([(60, 80, 75, 20, 25), (10,0,0,0,0), (5,0,0,0,0)], key=starsort, reverse=True)
# [(10, 0, 0, 0, 0), (60, 80, 75, 20, 25), (5, 0, 0, 0, 0)]
This shows the effect that more ratings can have upon the overall star value.
You'll find that this formula tends to give an overall rating which is a bit
lower than the overall rating reported by sites such as Amazon, Ebay or Wal-mart
particularly when there are few votes (say, less than 300). This reflects the
higher uncertainy that comes with fewer votes. As the number of votes increases
(into the thousands) all overall these rating formulas should tend to the
(weighted) average rating.
Since the formula only depends on the frequency distribution of 5-star ratings
for the item itself, it is easy to combine reviews from multiple sources (or,
update the overall rating in light of new votes) by simply adding the frequency
distributions together.
Unlike the IMDb formula, this formula does not depend on the average score
across all items, nor an artificial minimum number of votes cutoff value.
Moreover, this formula makes use of the full frequency distribution -- not just
the average number of stars and the number of votes. And it makes sense that it
should since an item with ten 5-stars and ten 1-stars should be treated as
having more uncertainty than (and therefore not rated as highly as) an item with
twenty 3-star ratings:
In [78]: starsort((10,0,0,0,10))
Out[78]: 2.386028063783418
In [79]: starsort((0,0,20,0,0))
Out[79]: 2.795342687927806
The IMDb formula does not take this into account.