boolean[] vs. BitSet: Which is more efficient?

Question

What is more efficient in terms of memory and CPU usage — an array of booleans or a BitSet? Specific BitSet methods are not used, only get/set/clear (==, =, Arrays.fill respectively for an array).

Woebegone

Answer 1

From some benchmarks with Sun JDK 1.6 computing primes with a sieve (best of 10 iterations to warm up, give the JIT compiler a chance, and exclude random scheduling delays, Core 2 Duo T5600 1.83GHz):

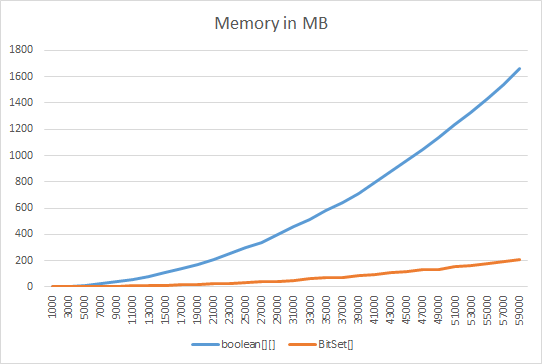
BitSet is more memory efficient than boolean[] except for very small sizes. Each boolean in the array takes a byte. The numbers from runtime.freeMemory() are a bit muddled for BitSet, but less.

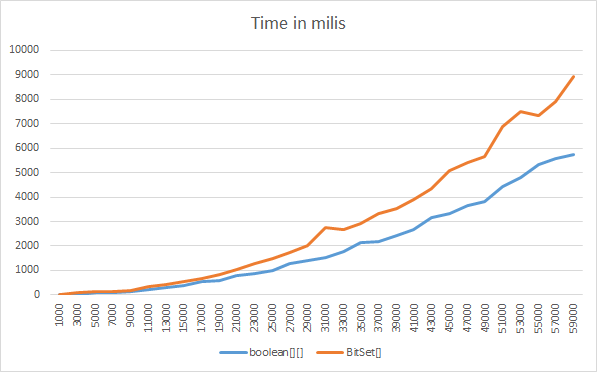
boolean[] is more CPU efficient except for very large sizes, where they are about even. E.g., for size 1 million boolean[] is about four times faster (e.g. 6ms vs 27ms), for ten and a hundred million they are about even.

Unsaddle

I suspect that some of the BitSet style operations (and, or, not) are faster as BitSet instead of array. Worth noting which operations are better. The title is going to mislead everyone into never using a BitSet again – Einsteinium

The test doesn't use set operations, and is biased towards writing. – Unsaddle

This is a misleading answer with no test code and a specific context. I encourage anybody reading this to read through the other answers here and think a little for themselves, about their specific situation. – Subaquatic

These are just facts from a particular benchmark, I don't see what is misleading about them. Of course, if this is important to you, do your own benchmarks for your particular situation. Personally I would prefer BitSet because it expresses intent, except if I had many runs with relatively small bit sets and a need to optimize for runtime. – Unsaddle

@Unsaddle Could you explain why for very large data, boolean[] and BitSet are about the same on CPU efficiency? It feels like boolean[] still should be more efficient. – Derangement

@Derangement Probably an effect of caching, so that for accesses to main memory you need to do read-update-write also when writing a byte. Notice that 1 million bytes, the largest size where boolean[] was faster, is about the size that could plausibly fit into a cache. – Unsaddle

Time complexity of BitSet#flip method: change the state of an arbitrarily long sequence of bits in constant time. - Effective Java, Joshua Bloch, Item #17 Minimize mutability – Jubbah

Answer 2

• Boolean[] uses about 4-20 bytes per boolean value.
• boolean[] uses about 1 byte per boolean value.
• BitSet uses about 1 bit per boolean value.

Memory size might not be an issue for you in which case boolean[] might be simpler to code.

Ronnyronsard

Note that 1 bit per boolean in the BitSet is the asymptotic value. Under the covers is uses a long[] so it is granulated into 64 bit chuncks. – Chondro

It' would be good to mention that usually you only need the 4 byte pointer per value. Because it's cached. Except you explicitly use new Boolean(); But of course it's way more than boolean[] – Apartheid

Boolean[] uses 4 or 8 bytes for each value, but definitely not up to 20 bytes. If you assume that the application creates a new Boolean object for each element (though there’s no reason to assume that), then most implementations would need 24 bytes for the object, which adds up to the 4 or 8 bytes for the reference, so even up to 32 bytes in total. But who would do that in practice… – Suspend

@Suspend any sane person would use autobixing but the default object header size on the OpenJDK is 12 bytes and on Zing its 8 bytes. With an 8 bytes alignment, the Boolean should be 16 bytes. – Ronnyronsard

Yes, the common implementation nowadays is with compressed class pointers, my bad. But the maximum header still is a header of 16 bytes, which makes a 24 bytes object and hence, 32 bytes for the object plus an uncompressed 64 bit reference. I’m not sure whether it makes sense to assume a sane person if they are using a Boolean[] array in a situation where boolean[] would suffice. Anyway, the phrase “uses about 4-20 bytes per boolean value” is misleading. – Suspend

Answer 3

Here you can see a Memory/Time benchmark comparing a boolean[][] trianguar matrix versus BitSet[] triangular matrix.

I create, set and read the (size * (size-1) / 2) values and compare memory usage and time...

Hope this help...

Here the code... (just a quikly dirty test code, sorry ;)

import java.util.BitSet;
import java.util.Date;

public class BooleanBitSetProfiler {

    Runtime runtime;
    int sum = 0;
    public void doIt() {

        runtime = Runtime.getRuntime();
        long[][] bitsetMatrix = new long[30][2];
        long[][] booleanMatrix = new long[30][2];
        int size = 1000;
        for (int i = 0; i < booleanMatrix.length; i++) {
            booleanMatrix[i] = testBooleanMatrix(size);
            bitsetMatrix[i] = testBitSet(size);
            size += 2000;
        }
        int debug = 1;
        for (int j = 0; j < booleanMatrix.length; j++){
            System.out.print(booleanMatrix[j][0] + ";");
        }
        System.out.println();
        for (int j = 0; j < booleanMatrix.length; j++){
            System.out.print(booleanMatrix[j][1] + ";");
        }
        System.out.println();
        for (int j = 0; j < bitsetMatrix.length; j++){
            System.out.print(bitsetMatrix[j][0] + ";");
        }
        System.out.println();
        for (int j = 0; j < bitsetMatrix.length; j++){
            System.out.print(bitsetMatrix[j][1] + ";");
        }
        System.out.println();
    }

    private long memory () {
        return runtime.totalMemory() - runtime.freeMemory();
    }
    private long[] testBooleanMatrix(int size) {
        runtime.gc();
        long startTime = new Date().getTime();
        long startMemory = memory();
        boolean[][] matrix = new boolean[size][];
        for (int i = 0; i < size; i++) {
            matrix[i] = new boolean[size - i - 1];
        }
        long creationMemory = memory();
        long creationTime = new Date().getTime();
        for (int i = 0; i < size; i++)  {
            for (int j = 0; j < matrix[i].length; j++) {
                matrix[i][j] = i % 2 == 0;
            }
        }
        long setMemory = memory();
        long setTime = new Date().getTime();
        for (int i = 0; i < size; i++)  {
            for (int j = 0; j < matrix[i].length; j++) {
                if (matrix[i][j]) sum++;
            }
        }
        long readTime = new Date().getTime();
        System.out.println("Boolean[][] (size " + size + ")");
        System.out.println("Creation memory " + printMem(creationMemory-startMemory) + ", set memory " + printMem(setMemory-startMemory));
        System.out.println("Creation time " + printTime(creationTime-startTime) + ", set time " + printTime(setTime - creationTime) + " read time " + printTime(readTime - setTime) + "\n");
        runtime.gc();
        return new long[]{(setMemory-startMemory)/(1024*1024), (readTime-startTime)};
    }
    private long[] testBitSet(int size) {
        runtime.gc();
        long startTime = new Date().getTime();
        long startMemory = memory();
        BitSet[] matrix = new BitSet[size];
        for (int i = 0; i < size; i++) {
            matrix[i] = new BitSet(size - i - 1);
        }
        long creationMemory = memory();
        long creationTime = new Date().getTime();
        for (int i = 0; i < size; i++)  {
            for (int j = 0; j < matrix[i].size(); j++) {
                matrix[i].set(j, (i % 2 == 0));
            }
        }
        long setMemory = memory();
        long setTime = new Date().getTime();
        for (int i = 0; i < size; i++)  {
            for (int j = 0; j < matrix[i].size(); j++) {
                if (matrix[i].get(j)) sum++;
            }
        }
        long readTime = new Date().getTime();
        System.out.println("BitSet[] (size " + size + ")");
        System.out.println("Creation memory " + printMem(creationMemory-startMemory) + ", set memory " + printMem(setMemory-startMemory));
        System.out.println("Creation time " + printTime(creationTime-startTime) + ", set time " + printTime(setTime - creationTime) + " read time " + printTime(readTime - setTime) + "\n");
        runtime.gc();
        return new long[]{(setMemory-startMemory)/(1024*1024), (readTime-startTime)};
    }

    private String printMem(long mem) {
        mem = mem / (1024*1024);
        return mem + "MB";
    }
    private String printTime(long milis) {
        int seconds = (int) (milis / 1000);
        milis = milis % 1000;
        return seconds > 0 ? seconds + "s " + milis + "ms" : milis + "ms";
    }
}

Betatron

Answer 4

A bit left-field of your question, but if storage is a concern you may want to look into Huffman compression. For example, 00000001 could be squeezed down by frequency to something equivalent to {(7)0, (1)1}. A more "randomized" string 00111010 would require a more complex representation, e.g. {(2)0, (3)1, (1)0, (1)1, (1)0}, and take up more space. Depending on the structure of your bit data, you may get some storage benefit from its use, beyond BitSet.

Endocardial

Answer 5

As for memory, the documentation for a BitSet has pretty clear implications. In particular:

Every bit set has a current size, which is the number of bits of space currently in use by the bit set. Note that the size is related to the implementation of a bit set, so it may change with implementation. The length of a bit set relates to logical length of a bit set and is defined independently of implementation.

The source for Java library classes is openly available and one can easily check this for themselves. In particular:

The internal field corresponding to the serialField "bits".
89 
90     private long[] words;

As for speed; it depends on what one is doing. In general, don't think about speed ahead of time; use whichever tool makes the most sense semantically and leads to the clearest code. Optimize only after observing that performance requirements aren't met and identifying bottlenecks.

Coming to SO and asking if A is faster than B is silly for many reasons, including but certainly not limited to:

1. It depends on the application, which nobody responding generally has access to. Analyze and profile it in the context it is being used in. Be sure that it's a bottleneck that's actually worth optimizing.
2. Questions like this that ask about speed generally show that the OP thinks they care about efficiency but wasn't willing to profile and didn't define performance requirements. Under the surface, that's usually a red flag that the OP is headed down the wrong path.

I know this is an old question but it came up recently; and I believe this is worth adding.

Subaquatic

Answer 6

It depends as always. Yes BitSet is more memory efficent, but as soon as you require multithreaded access boolean[] might be the better choice. For example for computing primes you only set the boolean to true and therefore you don't really need synchronization. Hans Boehm has written some paper about this and the same technique can be used for marking nodes in graph.

Epizoic

provided that your boolean array doesn't grow, that'd certainly be better for concurrent use. – Wyne

You'll still need synchronization to make sure that all threads see what the other threads have written. Here is a pretty good introduction. I'd love to read the paper by Hans Boehm - too bad the link is dead. – Icao

I think I found the paper by Hans Boehm: hpl.hp.com/techreports/2004/HPL-2004-209.pdf Result: You don't need synchronization. You just hope that the threads see what the others have done. It's no problem if they don't, they will simply be doing duplicate work. But in practice, the changes will usually be visible, and the algorithm will speed up linearly. – Icao

Answer 7

Going from Java to CPU is totally VM specific. For instance, it used to be that a boolean was actually implemented as a 32-bit value (quite probably is true to this day).

Unless you know it is going to matter you are better off writing the code to be clear, profile it, and then fix the parts that are slow or consuming a lot of memory.

You can do this as you go. For instance I once decided to not call .intern() on Strings because when I ran the code in the profiler it slowed it down too much (despite using less memory).

Ic

Answer 8

I believe that a BitSet is more memory- and CPU-efficient, is it can internally pack the bits into int, longs, or native data types, whereas a boolean[] requires a byte for each bit of data. Additionally, if you were to use the other methods (and, or, etc), you would find that the BitSet is more efficient, as there is no need to iterate through every element of an array; bitwise math is used instead.

Seafowl

Memory efficient - probably true. CPU efficient - most certainly not. It is almost always less efficient to perform two bitwise operations (shift/and or shift/or) and up to two memory accesses (though most likely cached) than a single memory access on x86. – Anisometropia

@EFraim: By reducing the amount of memory used you're increasing the chance of having everything in cache. Cache misses are very expensive. I wouldn't be at all surprised to see this factor make BitArray faster. – Adverb

For example: a bitset would outperform boolean[] if the whole bitset fits in the cache, but not the boolean[], and random access were required. – Carrew