Roc curve and cut off point. Python

Question

I ran a logistic regression model and made predictions of the logit values. I used this to get the points on the ROC curve:

 from sklearn import metrics
 fpr, tpr, thresholds = metrics.roc_curve(Y_test,p)

I know metrics.roc_auc_score gives the area under the ROC curve. Can anyone tell me what command will find the optimal cut-off point (threshold value)?

Ridinger

The answer to your question is simply, np.argmax(tpr - fpr) – Danielledaniels

And if you want the threshold value, its just thresholds[np.argmax(tpr - fpr)]. Everything else is verbosity. – Danielledaniels

Can anyone speak to the difference between thresholds[np.argmax(tpr - fpr)] and the most upvoted answer function threshold = Find_Optimal_Cutoff(data['true'], data['pred'])? The thresholds are close, but different when I do an actual calculation. – Wivinia

I would argue that to find the optimal point, you're looking for the balance point of sensitivity and specificity or, the tpr and 1-fpr. If you have a particular reason not to have the minimum difference between sensitivity and specificity, I can understand. To me though, the optimal point for the threshold value would be thresholds[np.argmin(abs(tpr-(1-fpr)))] – Josefajosefina

If you consider the optimal threshold to be the point on the curve closest to the top left corner of the ROC-AUC graph, you may use thresholds[np.argmin((1 - tpr) ** 2 + fpr ** 2)]. But @cgnorthcutt's solution maximizes the Youden's J statistic, which seems to be the more accepted method. What is truly "optimal" for your situation depends on the relative costs of false positives and false negatives. – Selfaddressed

I do not really understand why no one mentions here that the assumption everyone makes is that the cost of a False Positive is equal to a True Positive. This is not always the case. Only with this assumption this question can be answered with a single optimum in the way that is described here. Full explanation: en.wikipedia.org/wiki/Youden%27s_J_statistic – Pellucid

Answer 1

You can do this using the epi package in R, however I could not find similar package or example in Python.

The optimal cut off point would be where “true positive rate” is high and the “false positive rate” is low. Based on this logic, I have pulled an example below to find optimal threshold.

Python code:

import pandas as pd
import statsmodels.api as sm
import pylab as pl
import numpy as np
from sklearn.metrics import roc_curve, auc

# read the data in
df = pd.read_csv("http://www.ats.ucla.edu/stat/data/binary.csv")

# rename the 'rank' column because there is also a DataFrame method called 'rank'
df.columns = ["admit", "gre", "gpa", "prestige"]
# dummify rank
dummy_ranks = pd.get_dummies(df['prestige'], prefix='prestige')
# create a clean data frame for the regression
cols_to_keep = ['admit', 'gre', 'gpa']
data = df[cols_to_keep].join(dummy_ranks.iloc[:, 'prestige_2':])

# manually add the intercept
data['intercept'] = 1.0

train_cols = data.columns[1:]
# fit the model
result = sm.Logit(data['admit'], data[train_cols]).fit()
print result.summary()

# Add prediction to dataframe
data['pred'] = result.predict(data[train_cols])

fpr, tpr, thresholds =roc_curve(data['admit'], data['pred'])
roc_auc = auc(fpr, tpr)
print("Area under the ROC curve : %f" % roc_auc)

####################################
# The optimal cut off would be where tpr is high and fpr is low
# tpr - (1-fpr) is zero or near to zero is the optimal cut off point
####################################
i = np.arange(len(tpr)) # index for df
roc = pd.DataFrame({'fpr' : pd.Series(fpr, index=i),'tpr' : pd.Series(tpr, index = i), '1-fpr' : pd.Series(1-fpr, index = i), 'tf' : pd.Series(tpr - (1-fpr), index = i), 'thresholds' : pd.Series(thresholds, index = i)})
roc.iloc[(roc.tf-0).abs().argsort()[:1]]

# Plot tpr vs 1-fpr
fig, ax = pl.subplots()
pl.plot(roc['tpr'])
pl.plot(roc['1-fpr'], color = 'red')
pl.xlabel('1-False Positive Rate')
pl.ylabel('True Positive Rate')
pl.title('Receiver operating characteristic')
ax.set_xticklabels([])

The optimal cut off point is 0.317628, so anything above this can be labeled as 1 else 0. You can see from the output/chart that where TPR is crossing 1-FPR the TPR is 63%, FPR is 36% and TPR-(1-FPR) is nearest to zero in the current example.

Output:

        1-fpr       fpr        tf     thresholds       tpr
  171  0.637363  0.362637  0.000433    0.317628     0.637795

Hope this is helpful.

Edit

To simplify and bring in re-usability, I have made a function to find the optimal probability cutoff point.

Python Code:

def Find_Optimal_Cutoff(target, predicted):
    """ Find the optimal probability cutoff point for a classification model related to event rate
    Parameters
    ----------
    target : Matrix with dependent or target data, where rows are observations

    predicted : Matrix with predicted data, where rows are observations

    Returns
    -------     
    list type, with optimal cutoff value
        
    """
    fpr, tpr, threshold = roc_curve(target, predicted)
    i = np.arange(len(tpr)) 
    roc = pd.DataFrame({'tf' : pd.Series(tpr-(1-fpr), index=i), 'threshold' : pd.Series(threshold, index=i)})
    roc_t = roc.iloc[(roc.tf-0).abs().argsort()[:1]]

    return list(roc_t['threshold']) 


# Add prediction probability to dataframe
data['pred_proba'] = result.predict(data[train_cols])

# Find optimal probability threshold
threshold = Find_Optimal_Cutoff(data['admit'], data['pred_proba'])
print threshold
# [0.31762762459360921]

# Find prediction to the dataframe applying threshold
data['pred'] = data['pred_proba'].map(lambda x: 1 if x > threshold else 0)

# Print confusion Matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(data['admit'], data['pred'])
# array([[175,  98],
#        [ 46,  81]])

Outdoors

Is there a simple method to apply this threshold value to the predictions? Or do you just use an apply type function on the data['preds']? – Azevedo

@ skmathur, I have made it as a function for re-usability & simplification. Hope this helps. – Outdoors

There's a problem with your formula for Youden's Index in the Find_Optimal_Cutoff function. roc_curve returns fpr which is the false positive rate (1-specificity). You're subtracting (1-fpr). You need to change the tpr-(1-fpr) to tpr-fpr. – Handsel

Epi package in R chooses the cutoff that maximizes (specificity + sensitivity). Hence, it should be tpr + (1-fpr) and not tpr - (1-fpr) as given in the code – Lachish

@JohnBonfardeci Is it just me? I have the feeling OPs solution is producing the wrong result .. Shouldn't it be pd.Series(tpr-fpr, index=thresholds, name='tf').idxmax() ? – Christiechristin

If applying this method to MNLogit with binary outcome, change the line fpr, tpr, thresholds =roc_curve(data['admit'], data['pred']) to fpr, tpr, thresholds =roc_curve(data['admit'], data['pred'][:, 1]). – Uniformity

I don't understand why this reply has the most upvotes. @JohnBonfardeci and @ StefanFalk are right, the formula is incorrect. Besides that, the axis discribtions of the plot are also wrong, there should be a double y-axis or a legend for the tpr and fpr and the x-axis is actually the thresholds. – Gaiser

Answer 2

Given tpr, fpr, thresholds from your question, the answer for the optimal threshold is just:

optimal_idx = np.argmax(tpr - fpr)
optimal_threshold = thresholds[optimal_idx]

Danielledaniels

what if I get negative optimal_threshold ...., My output prediction is in the range [0,1]... – Edulcorate

Using optimal_idx = np.argmax(tpr - fpr) optimal_threshold = thresholds[optimal_idx] as suggested does not work for me. The thresholds array contains negative values, but I expected values between 0 and 1. – Lona

@rafaelcaballero "does not work"? Everything you described sounds like it's working correctly. It should not be between 0 and 1. It's just a score. – Danielledaniels

Then I missunderstood the question. I thought that the threshold moved between 0 and 1, and that the goal was to find the value in this range that maximized tpr-fpr – Lona

@Danielledaniels Your code is correct. But TPR = TP/(real positive), FPR = FP/(real negative). TPR + FPR != 1. – Weldonwelfare

@Weldonwelfare - Yup. That's why I say "it should not be between 0 and 1. It's just a score," above. Its a good point, though. Thanks for reminding. – Danielledaniels

Answer 3

Vanilla Python Implementation of Youden's J-Score

def cutoff_youdens_j(fpr,tpr,thresholds):
    j_scores = tpr-fpr
    j_ordered = sorted(zip(j_scores,thresholds))
    return j_ordered[-1][1]

Retention

Answer 4

Another possible solution.

I'll create some random data.

import numpy as np
import pandas as pd
import scipy.stats as sps
from sklearn import linear_model
from sklearn.metrics import roc_curve, RocCurveDisplay, auc
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import seaborn as sns

# define data distributions
N0 = 300
N1 = 250

dist0 = sps.gamma(a=8, scale=1/10)
x0 = np.linspace(dist0.ppf(0), dist0.ppf(1-1e-5), 100)
y0 = dist0.pdf(x0)

dist1 = sps.gamma(a=15, scale=1/10)
x1 = np.linspace(dist1.ppf(0), dist1.ppf(1-1e-5), 100)
y1 = dist1.pdf(x1)

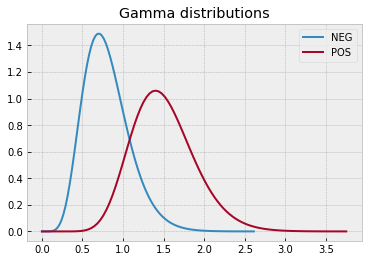
with plt.style.context("bmh"):
    plt.plot(x0, y0, label="NEG")
    plt.plot(x1, y1, label="POS")
    plt.legend()
    plt.title("Gamma distributions")

# create a random dataset
rvs0 = dist0.rvs(N0, random_state=0)
rvs1 = dist1.rvs(N1, random_state=1)

with plt.style.context("bmh"):
    plt.hist(rvs0, alpha=.5, label="NEG")
    plt.hist(rvs1, alpha=.5, label="POS")
    plt.legend()
    plt.title("Random dataset")

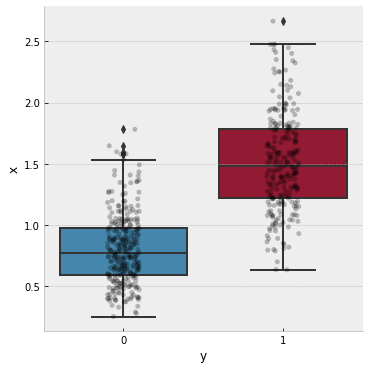
Initialize a dataframe with observations (x feature and y target)

df = pd.DataFrame({
    "y": np.concatenate(( np.repeat(0, N0) , np.repeat(1, N1) )),
    "x": np.concatenate(( rvs0             , rvs1             )),
})

and display it with a box plot

# plot the data
with plt.style.context("bmh"):
    g = sns.catplot(
        kind="box",
        data=df,
        x="y", y="x"
    )
    ax = g.axes.flat[0]
    sns.stripplot(
        data=df,
        x="y", y="x",
        ax=ax, color='k',
        alpha=.25
    )
    plt.show()

Now, we can split the dataframe into train-test, perform Logistic regression, compute ROC curve, AUC, Youden's index, find the cut-off and plot everything. All using pandas

# split dataset into train-test
X_train, X_test, y_train, y_test = train_test_split(
    df[["x"]], df.y.values, test_size=0.5, random_state=1)
# init and fit Logistic Regression on train set
clf = linear_model.LogisticRegression()
clf.fit(X_train, y_train)
# predict probabilities on x test set
y_proba = clf.predict_proba(X_test)
# compute FPR and TPR from y test set and predicted probabilities
fpr, tpr, thresholds = roc_curve(
    y_test, y_proba[:,1], drop_intermediate=False)
# compute ROC AUC
roc_auc = auc(fpr, tpr)
# init a dataframe for results
df_test = pd.DataFrame({
    "x": X_test.x.values.flatten(),
    "y": y_test,
    "proba": y_proba[:,1]
})
# sort it by predicted probabilities
# because thresholds[1:] = y_proba[::-1]
df_test.sort_values(by="proba", inplace=True)
# add reversed TPR and FPR
df_test["tpr"] = tpr[1:][::-1]
df_test["fpr"] = fpr[1:][::-1]
# optional: add thresholds to check
#df_test["thresholds"] = thresholds[1:][::-1]
# add Youden's j index
df_test["youden_j"] = df_test.tpr - df_test.fpr
# define the cut_off and diplay it
cut_off = df_test.sort_values(
    by="youden_j", ascending=False, ignore_index=True).iloc[0]
print("CUT-OFF:")
print(cut_off)

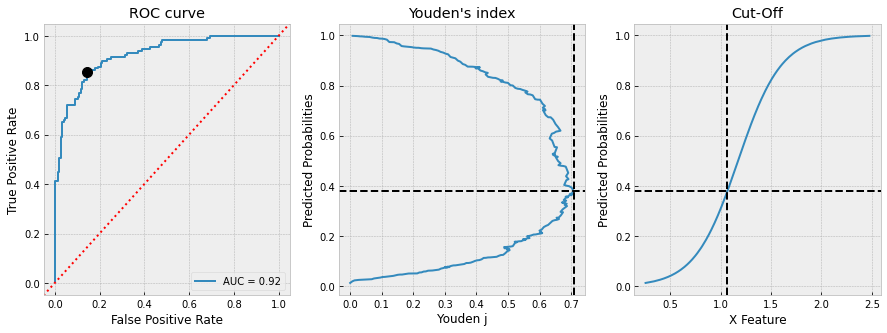
# plot everything
with plt.style.context("bmh"):
    fig, ax = plt.subplots(1, 3, figsize=(15, 5))
    
    RocCurveDisplay(
        fpr=df_test.fpr, tpr=df_test.tpr,
        roc_auc=roc_auc).plot(ax=ax[0])
    ax[0].set_title("ROC curve")
    ax[0].axline(xy1=(0,0), slope=1, color="r", ls=":")
    ax[0].plot(cut_off.fpr, cut_off.tpr, 'ko', ms=10)
    
    df_test.plot(
        x="youden_j", y="proba", ax=ax[1], 
        ylabel="Predicted Probabilities", xlabel="Youden j",
        title="Youden's index", legend=False
    )
    ax[1].axvline(cut_off.youden_j, color="k", ls="--")
    ax[1].axhline(cut_off.proba, color="k", ls="--")
    
    df_test.plot(
        x="x", y="proba", ax=ax[2], 
        ylabel="Predicted Probabilities", xlabel="X Feature",
        title="Cut-Off", legend=False
    )
    ax[2].axvline(cut_off.x, color="k", ls="--")
    ax[2].axhline(cut_off.proba, color="k", ls="--")

    plt.show()

and we get

CUT-OFF:
x           1.065712
y           1.000000
proba       0.378543
tpr         0.852713
fpr         0.143836
youden_j    0.708878

We can finally check

# check results
TP = df_test[(df_test.x>=cut_off.x)&(df_test.y==1)].index.size
FP = df_test[(df_test.x>=cut_off.x)&(df_test.y==0)].index.size
TN = df_test[(df_test.x< cut_off.x)&(df_test.y==0)].index.size
FN = df_test[(df_test.x< cut_off.x)&(df_test.y==1)].index.size

print("True Positive Rate: ", TP / (TP + FN))
print("False Positive Rate:", 1 - TN / (TN + FP))

True Positive Rate:  0.8527131782945736
False Positive Rate: 0.14383561643835618

Topsoil

This is a nice approach, it does however not account for non unique probabilites. roc_curve returns a value for each unique probability, yet the line df_test["tpr"] = tpr[1:][::-1] error, for any df that was created with unique y_proba – Prepotent

I suggest, dropping all duplicates regarding to the column "proba" in df_test right after its creation. – Prepotent

Answer 5

Although I am late to the party, but you can also use Geometric Mean to determine the optimal threshold as stated here: threshold tuning for imbalance classification

It can be computed as:

# calculate the g-mean for each threshold
gmeans = sqrt(tpr * (1-fpr))
# locate the index of the largest g-mean
ix = argmax(gmeans)
print('Best Threshold=%f, G-Mean=%.3f' % (thresholds[ix], gmeans[ix]))

October

Use of sqrt seems unnecessary here. Argmax works same without it. – Laurencelaurene

What optimal does it give us? Wouldn't it contradict with Youden's index for this example: tpr=0.5 & fpr=0.5 and tpr=0.55 & fpr=0.45? – Encephalic