cocktail party algorithm SVD implementation ... in one line of code?

Question

In a slide within the introductory lecture on machine learning by Stanford's Andrew Ng at Coursera, he gives the following one line Octave solution to the cocktail party problem given the audio sources are recorded by two spatially separated microphones:

[W,s,v]=svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');

At the bottom of the slide is "source: Sam Roweis, Yair Weiss, Eero Simoncelli" and at the bottom of an earlier slide is "Audio clips courtesy of Te-Won Lee". In the video, Professor Ng says,

"So you might look at unsupervised learning like this and ask, 'How complicated is it to implement this?' It seems like in order to build this application, it seems like to do this audio processing, you would write a ton of code, or maybe link into a bunch of C++ or Java libraries that process audio. It seems like it would be a really complicated program to do this audio: separating out audio and so on. It turns out the algorithm to do what you just heard, that can be done with just one line of code ... shown right here. It did take researchers a long time to come up with this line of code. So I'm not saying this is an easy problem. But it turns out that when you use the right programming environment many learning algorithms will be really short programs."

The separated audio results played in the video lecture are not perfect but, in my opinion, amazing. Does anyone have any insight on how that one line of code performs so well? In particular, does anyone know of a reference that explains the work of Te-Won Lee, Sam Roweis, Yair Weiss, and Eero Simoncelli with respect to that one line of code?

UPDATE

To demonstrate the algorithm's sensitivity to microphone separation distance, the following simulation (in Octave) separates the tones from two spatially separated tone generators.

% define model 
f1 = 1100;              % frequency of tone generator 1; unit: Hz 
f2 = 2900;              % frequency of tone generator 2; unit: Hz 
Ts = 1/(40*max(f1,f2)); % sampling period; unit: s 
dMic = 1;               % distance between microphones centered about origin; unit: m 
dSrc = 10;              % distance between tone generators centered about origin; unit: m 
c = 340.29;             % speed of sound; unit: m / s 

% generate tones
figure(1);
t = [0:Ts:0.025];
tone1 = sin(2*pi*f1*t);
tone2 = sin(2*pi*f2*t);
plot(t,tone1); 
hold on;
plot(t,tone2,'r'); xlabel('time'); ylabel('amplitude'); axis([0 0.005 -1 1]); legend('tone 1', 'tone 2');
hold off;

% mix tones at microphones
% assume inverse square attenuation of sound intensity (i.e., inverse linear attenuation of sound amplitude)
figure(2);
dNear = (dSrc - dMic)/2;
dFar = (dSrc + dMic)/2;
mic1 = 1/dNear*sin(2*pi*f1*(t-dNear/c)) + \
       1/dFar*sin(2*pi*f2*(t-dFar/c));
mic2 = 1/dNear*sin(2*pi*f2*(t-dNear/c)) + \
       1/dFar*sin(2*pi*f1*(t-dFar/c));
plot(t,mic1);
hold on;
plot(t,mic2,'r'); xlabel('time'); ylabel('amplitude'); axis([0 0.005 -1 1]); legend('mic 1', 'mic 2');
hold off;

% use svd to isolate sound sources
figure(3);
x = [mic1' mic2'];
[W,s,v]=svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');
plot(t,v(:,1));
hold on;
maxAmp = max(v(:,1));
plot(t,v(:,2),'r'); xlabel('time'); ylabel('amplitude'); axis([0 0.005 -maxAmp maxAmp]); legend('isolated tone 1', 'isolated tone 2');
hold off;

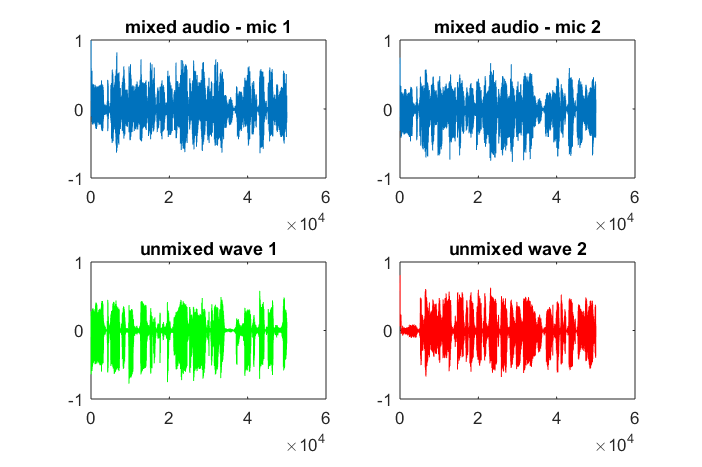
After about 10 minutes of execution on my laptop computer, the simulation generates the following three figures illustrating the two isolated tones have the correct frequencies.

However, setting the microphone separation distance to zero (i.e., dMic = 0) causes the simulation to instead generate the following three figures illustrating the simulation could not isolate a second tone (confirmed by the single significant diagonal term returned in svd's s matrix).

I was hoping the microphone separation distance on a smartphone would be large enough to produce good results but setting the microphone separation distance to 5.25 inches (i.e., dMic = 0.1333 meters) causes the simulation to generate the following, less than encouraging, figures illustrating higher frequency components in the first isolated tone.

Petulia

I have vague memories of this lecture, but can't remember what x is; is it the spectrogram of the waveform, or what? – Woofer

Professor Ng, at t=5:30 in the introductory video 4 on unsupervised learning, seems to suggest that x is a vector of the audio samples. Perhaps that repmat section in the svd argument is implementing some sort of power normalization of the signal. – Petulia

Answer 1

I was trying to figure this out as well, 2 years later. But I got my answers; hopefully it'll help someone.

You need 2 audio recordings. You can get audio examples from http://research.ics.aalto.fi/ica/cocktail/cocktail_en.cgi.

reference for implementation is http://www.cs.nyu.edu/~roweis/kica.html

ok, here's code -

[x1, Fs1] = audioread('mix1.wav');
[x2, Fs2] = audioread('mix2.wav');
xx = [x1, x2]';
yy = sqrtm(inv(cov(xx')))*(xx-repmat(mean(xx,2),1,size(xx,2)));
[W,s,v] = svd((repmat(sum(yy.*yy,1),size(yy,1),1).*yy)*yy');

a = W*xx; %W is unmixing matrix
subplot(2,2,1); plot(x1); title('mixed audio - mic 1');
subplot(2,2,2); plot(x2); title('mixed audio - mic 2');
subplot(2,2,3); plot(a(1,:), 'g'); title('unmixed wave 1');
subplot(2,2,4); plot(a(2,:),'r'); title('unmixed wave 2');

audiowrite('unmixed1.wav', a(1,:), Fs1);
audiowrite('unmixed2.wav', a(2,:), Fs1);

Filament

Are you able to locate a reference that explains more explicitly the rationale for that line of code? – Wayless

Could you please explain how the signal mixing work inside the link you provided? Using your code it is good to extract two sound sources from the two mixed files downloaded from the site. However, when I try to mix two separate signals together myself, it seems the algorithm cannot output the correct result. I am using the naive way to get the mixed signals: mic1 = 0.3 * track1 + 0.5 * track2, mic2 = 0.5 * track1 + 0.3 * track2. These are the signal I tried to feed to the algorithm. Thank you very much! – Epicurean

I am kinda new to Matlab. I am having errors in line 3 saying it has problem concatenating 2 matrix of different dimensions. How should I handle this problem? – Crinkleroot

I tried that code but it does not work very well... (not blaming you!!) – United

Answer 2

x(t) is the original voice from one channel/microphone.

X = repmat(sum(x.*x,1),size(x,1),1).*x)*x' is an estimation of the power spectrum of x(t). Although X' = X, the intervals between rows and columns are not the same at all. Each row represents the time of the signal, while each column is frequency. I guess this is an estimation and simplification of a more strict expression called spectrogram.

Singular Value Decomposition on spectrogram is used to factorize the signal into different components based on spectrum information. Diagonal values in s are the magnitude of different spectrum components. The rows in u and columns in v' are the orthogonal vectors that map the frequency component with the corresponding magnitude to X space.

I don't have voice data to test, but in my understanding, by means of SVD, the components fall into the similar orthogonal vectors are hopefully be clustered with the help of unsupervised learning. Say, if the first 2 diagonal magnitudes from s are clustered, then u*s_new*v' will form the one-person-voice, where s_new is the same of s except all the elements at (3:end,3:end) are eliminated.

Two articles about the sound-formed matrix and SVD are for your reference.

Liveried

gregS, mathematically an n-by-2 matrix x can still form an X with the repmat operation. However, the spectrogram can only show channel each time. So I think it makes more sense to use n-by-1 x each time, and treat the problem as a linear regression (two matrix equations). Another two possible approachs are (i) to average two channels as n-by-2 x; or (ii) binding them together to construct an 2*n-by-2 x. – Liveried

gregS, I reconsidered your question. It may work if you implement repmat on a n-by-2 x. Physically it can be viewed as an average of power from two channels at each time, and each frequency. – Liveried

I found this post after watching the introduction video of Machine Learning (the course has just begun again). I was wondering if you managed to reproduce the audio separation shown in the video, or if it was developed during the course. – Philpot

@Philpot please search Andrew Ng's publication on unsupervised/deep learning on audio, thanks – Liveried

You can find speech examples here mcdermottlab.mit.edu/cocktail_examples/index.html – Thrilling

Why is $X$ the power of spectrum of $x$? Also according to the answer of Jack Z, $x$ is not the original voice from the recording but some kind of processed reciprocal of the eigenvalue of the covariance of the original voice. – Wayless

The line yy = sqrtm(inv(cov(xx')))*(xx-repmat(mean(xx,2),1,size(xx,2))); should be yy = ( sqrtm(inv(cov(xx')))*(xx-repmat(mean(xx,2),1,size(xx,2))) ) '; right? In the question the matrix x that underwent the svd operation was an n x 2 matrix, whereas the yy in the answer that underwent the svd is a 2 x n matrix. – Neurilemma