I found this implementation which can be used as a drop-in replacement for texture() (from http://www.java-gaming.org/index.php?topic=35123.0 (one typo fixed)):
// from http://www.java-gaming.org/index.php?topic=35123.0
vec4 cubic(float v){
vec4 n = vec4(1.0, 2.0, 3.0, 4.0) - v;
vec4 s = n * n * n;
float x = s.x;
float y = s.y - 4.0 * s.x;
float z = s.z - 4.0 * s.y + 6.0 * s.x;
float w = 6.0 - x - y - z;
return vec4(x, y, z, w) * (1.0/6.0);
}
vec4 textureBicubic(sampler2D sampler, vec2 texCoords){
vec2 texSize = textureSize(sampler, 0);
vec2 invTexSize = 1.0 / texSize;
texCoords = texCoords * texSize - 0.5;
vec2 fxy = fract(texCoords);
texCoords -= fxy;
vec4 xcubic = cubic(fxy.x);
vec4 ycubic = cubic(fxy.y);
vec4 c = texCoords.xxyy + vec2 (-0.5, +1.5).xyxy;
vec4 s = vec4(xcubic.xz + xcubic.yw, ycubic.xz + ycubic.yw);
vec4 offset = c + vec4 (xcubic.yw, ycubic.yw) / s;
offset *= invTexSize.xxyy;
vec4 sample0 = texture(sampler, offset.xz);
vec4 sample1 = texture(sampler, offset.yz);
vec4 sample2 = texture(sampler, offset.xw);
vec4 sample3 = texture(sampler, offset.yw);
float sx = s.x / (s.x + s.y);
float sy = s.z / (s.z + s.w);
return mix(
mix(sample3, sample2, sx), mix(sample1, sample0, sx)
, sy);
}
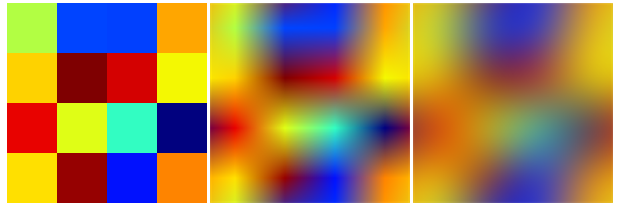
Example: Nearest, bilinear, bicubic:
![enter image description here]()
The ImageData of this image is
{{{0.698039, 0.996078, 0.262745}, {0., 0.266667, 1.}, {0.00392157,
0.25098, 0.996078}, {1., 0.65098, 0.}}, {{0.996078, 0.823529,
0.}, {0.498039, 0., 0.00392157}, {0.831373, 0.00392157,
0.00392157}, {0.956863, 0.972549, 0.00784314}}, {{0.909804,
0.00784314, 0.}, {0.87451, 0.996078, 0.0862745}, {0.196078,
0.992157, 0.760784}, {0.00392157, 0.00392157, 0.498039}}, {{1.,
0.878431, 0.}, {0.588235, 0.00392157, 0.00392157}, {0.00392157,
0.0666667, 0.996078}, {0.996078, 0.517647, 0.}}}
I tried to reproduce this (many other interpolation techniques)
![enter image description here]()
but they have clamped padding, while I have repeating (wrapping) boundaries. Therefore it is not exactly the same.
It seems this bicubic business is not a proper interpolation, i.e. it does not take on the original values at the points where the data is defined.